Максимальное ожидание в Matlab при отсутствии данных

Я должен использовать EM для оценки среднего значения и ковариации гауссовского распределения для каждого из двух классов. У них тоже есть некоторые недостающие атрибуты.

Классы каждого объекта известны. Поэтому проблема в основном сводится к подгонке гауссовой модели с отсутствующим элементом.

Какую библиотеку лучше всего использовать?

Чем алгоритм ECM отличается от алгоритма EM?

Источник

3 ответа

Решение

Спасибо всем. Но я использую ecmnmle для оценки параметров, а затем для получения распределения маргиналов, которое позже будет использовано в байесовской классификации. Это работает довольно хорошо с точностью 0,9 и 0,69 на 2 классах.

Источник

Если у вас есть доступ к панели инструментов статистики, вы можете использовать класс GMDISTRIBUTION, чтобы соответствовать гауссовой модели смеси, используя алгоритм EM.

Вот пример:

%# sample dataset
load fisheriris
data = meas(:,1:2);
label = species;

%# fit GMM using EM
K = 2;
obj = gmdistribution.fit(data, K);

%# assign points to mixtures: argmax_k P(M(k)|data)
P = posterior(obj, data);
[~,mIDX] = max(P,[],2);

%# GMM components
obj.mu             %# means
obj.Sigma          %# covariances
obj.PComponents    %# mixture weights

%# visualize original data clusters
figure
gscatter(data(:,1), data(:,2), label)

%# visualize mixtures found
figure
gscatter(data(:,1), data(:,2), mIDX), hold on
ezcontour(@(x,y)pdf(obj,[x y]), xlim(), ylim())

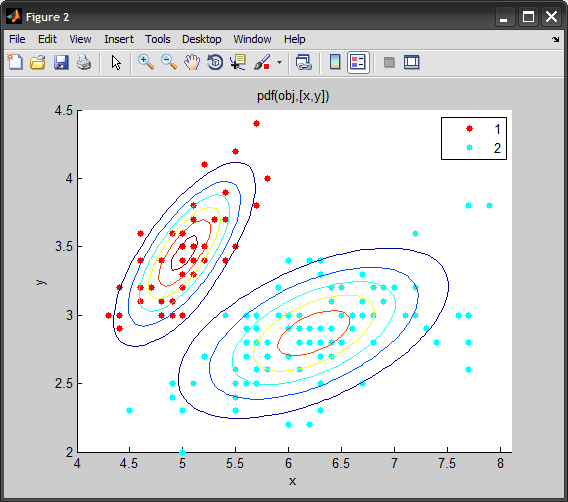
Если нет, попробуйте отличный Netlab Toolbox, так как он имеет реализацию GMM.

Источник

Пожалуйста, взгляните на инструментарий PMTK

Вот реализация EM (подходит смесь гауссиан, где данные могут иметь записи NaN)

Источник
Другие вопросы по тегам