pykalman: (по умолчанию) обработка пропущенных значений

Question

Я использую KalmanFilter из модуля pykalman, и мне было интересно, как он справляется с отсутствующими наблюдениями. Согласно документации:

В реальных системах часто случается, что датчики иногда выходят из строя. Фильтр Калмана, алгоритм Калмана Смолтера и ЭМ все оснащены для обработки этого сценария. Чтобы использовать его, нужно только применить маску NumPy к измерению на недостающем временном шаге:

из импортного импорта ma X = ma.array ([1,2,3]) X 1 = ma.masked # скрыть измерение на шаге 1 времени kf.em(X).smooth(X)

мы могли бы сгладить входные временные ряды. Так как это "дополнительная" функция, я предполагаю, что она не выполняется автоматически; так каков подход по умолчанию при наличии NaN в переменных?

Теоретический подход к тому, что может произойти, объясняется здесь; это то, что делает pykalman (что было бы действительно здорово на мой взгляд):

Перекрестная проверка - Как обрабатывать неполные данные в Kalman Filter?

Answer 1

Давайте посмотрим на исходный код:

В функции filter_update pykalman проверяет, маскируется ли текущее наблюдение или нет.

def filter_update(...)

        # Make a masked observation if necessary
        if observation is None:
            n_dim_obs = observation_covariance.shape[0]
            observation = np.ma.array(np.zeros(n_dim_obs))
            observation.mask = True
        else:
            observation = np.ma.asarray(observation) 

Это не влияет на шаг прогнозирования. Но у шага коррекции есть два варианта. Это происходит в функции _filter_correct.

def _filter_correct(...)

    if not np.any(np.ma.getmask(observation)):

         # the normal Kalman Filter math

    else:
        n_dim_state = predicted_state_covariance.shape[0]
        n_dim_obs = observation_matrix.shape[0]
        kalman_gain = np.zeros((n_dim_state, n_dim_obs))

        # !!!! the corrected state takes the result of the prediction !!!!

        corrected_state_mean = predicted_state_mean
        corrected_state_covariance = predicted_state_covariance

Итак, как вы можете видеть, это именно теоретический подход.

Вот краткий пример и рабочие данные для игры.

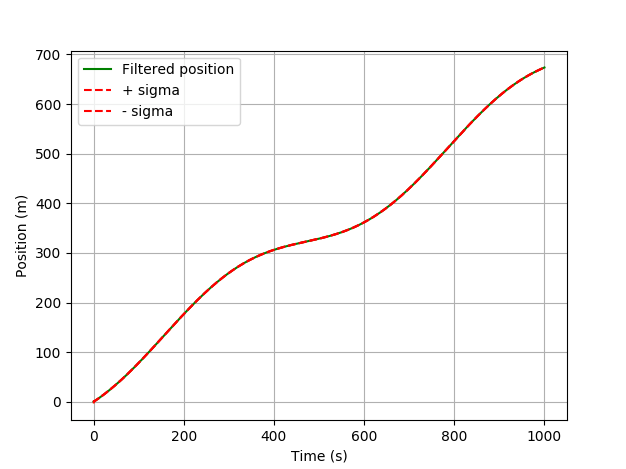
Предположим, у вас есть GPS-приемник, и вы хотите отслеживать себя во время ходьбы. Приемник обладает хорошей точностью. Для упрощения предположим, что вы идете прямо вперед.

Ничего интересного не происходит. Фильтр очень хорошо оценивает вашу позицию из-за хорошего сигнала GPS. Что произойдет, если у вас некоторое время нет сигнала?

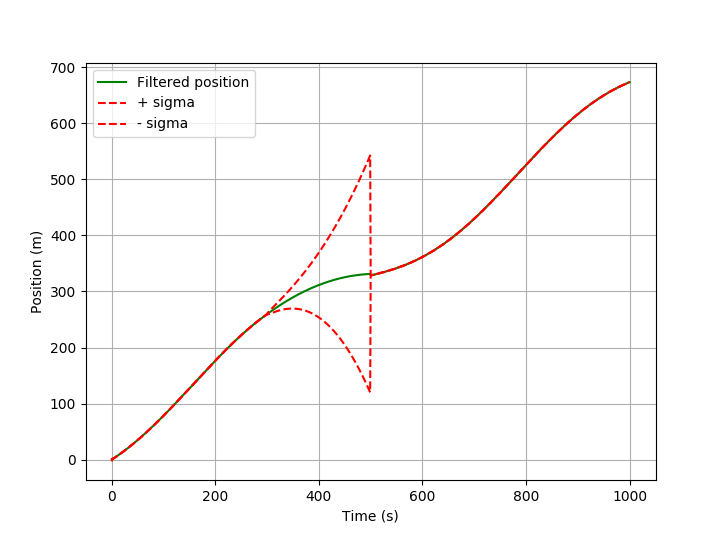
Фильтр может прогнозировать только на основе существующего состояния и знаний о динамике системы (см. Матрицу Q). С каждым шагом прогнозирования неопределенность растет. Диапазон 1-сигма вокруг предполагаемой позиции становится больше. Как только новое наблюдение снова появляется, состояние исправляется.

Вот код и данные:

from pykalman import KalmanFilter
import numpy as np
import matplotlib.pyplot as plt
from numpy import ma

# enable or disable missing observations
use_mask = 1

# reading data (quick and dirty)
Time=[]
X=[]

for line in open('data/dataset_01.csv'):
    f1, f2  = line.split(';')
    Time.append(float(f1))
    X.append(float(f2))

if (use_mask):
    X = ma.asarray(X)
    X[300:500] = ma.masked

# Filter Configuration

# time step
dt = Time[2] - Time[1]

# transition_matrix  
F = [[1,  dt,   0.5*dt*dt], 
     [0,   1,          dt],
     [0,   0,           1]]  

# observation_matrix   
H = [1, 0, 0]

# transition_covariance 
Q = [[   1,     0,     0], 
     [   0,  1e-4,     0],
     [   0,     0,  1e-6]] 

# observation_covariance 
R = [0.04] # max error = 0.6m

# initial_state_mean
X0 = [0,
      0,
      0]

# initial_state_covariance
P0 = [[ 10,    0,   0], 
      [  0,    1,   0],
      [  0,    0,   1]]

n_timesteps = len(Time)
n_dim_state = 3

filtered_state_means = np.zeros((n_timesteps, n_dim_state))
filtered_state_covariances = np.zeros((n_timesteps, n_dim_state, n_dim_state))

# Kalman-Filter initialization
kf = KalmanFilter(transition_matrices = F, 
                  observation_matrices = H, 
                  transition_covariance = Q, 
                  observation_covariance = R, 
                  initial_state_mean = X0, 
                  initial_state_covariance = P0)


# iterative estimation for each new measurement
for t in range(n_timesteps):
    if t == 0:
        filtered_state_means[t] = X0
        filtered_state_covariances[t] = P0
    else:
        filtered_state_means[t], filtered_state_covariances[t] = (
        kf.filter_update(
            filtered_state_means[t-1],
            filtered_state_covariances[t-1],
            observation = X[t])
        )

position_sigma = np.sqrt(filtered_state_covariances[:, 0, 0]);        

# plot of the resulted trajectory        
plt.plot(Time, filtered_state_means[:, 0], "g-", label="Filtered position", markersize=1)
plt.plot(Time, filtered_state_means[:, 0] + position_sigma, "r--", label="+ sigma", markersize=1)
plt.plot(Time, filtered_state_means[:, 0] - position_sigma, "r--", label="- sigma", markersize=1)
plt.grid()
plt.legend(loc="upper left")
plt.xlabel("Time (s)")
plt.ylabel("Position (m)")
plt.show()      

ОБНОВИТЬ

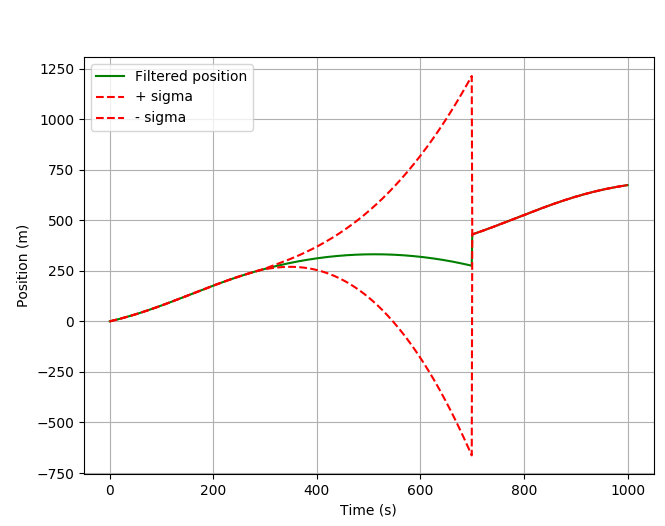
Это выглядит еще интереснее, если вы маскируете более длительный период (300:700).

Как видите, позиция возвращается. Это происходит из-за переходной матрицы F, которая связывает прогноз для положения, скорости и ускорения.

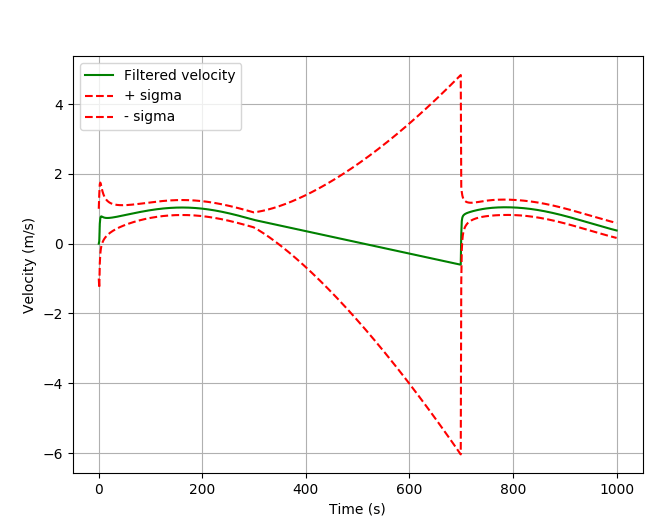
Если вы посмотрите на состояние скорости, это объясняет убывающую позицию.

В момент времени 300 с ускорение останавливается. Скорость снижается с постоянным наклоном и пересекает значение 0. После этой временной точки позиция должна вернуться.

Для построения скорости используйте следующий код:

velocity_sigma = np.sqrt(filtered_state_covariances[:, 1, 1]);     

# plot of the estimated velocity        
plt.plot(Time, filtered_state_means[:, 1], "g-", label="Filtered velocity", markersize=1)
plt.plot(Time, filtered_state_means[:, 1] + velocity_sigma, "r--", label="+ sigma", markersize=1)
plt.plot(Time, filtered_state_means[:, 1] - velocity_sigma, "r--", label="- sigma", markersize=1)
plt.grid()
plt.legend(loc="upper left")
plt.xlabel("Time (s)")
plt.ylabel("Velocity (m/s)")
plt.show()