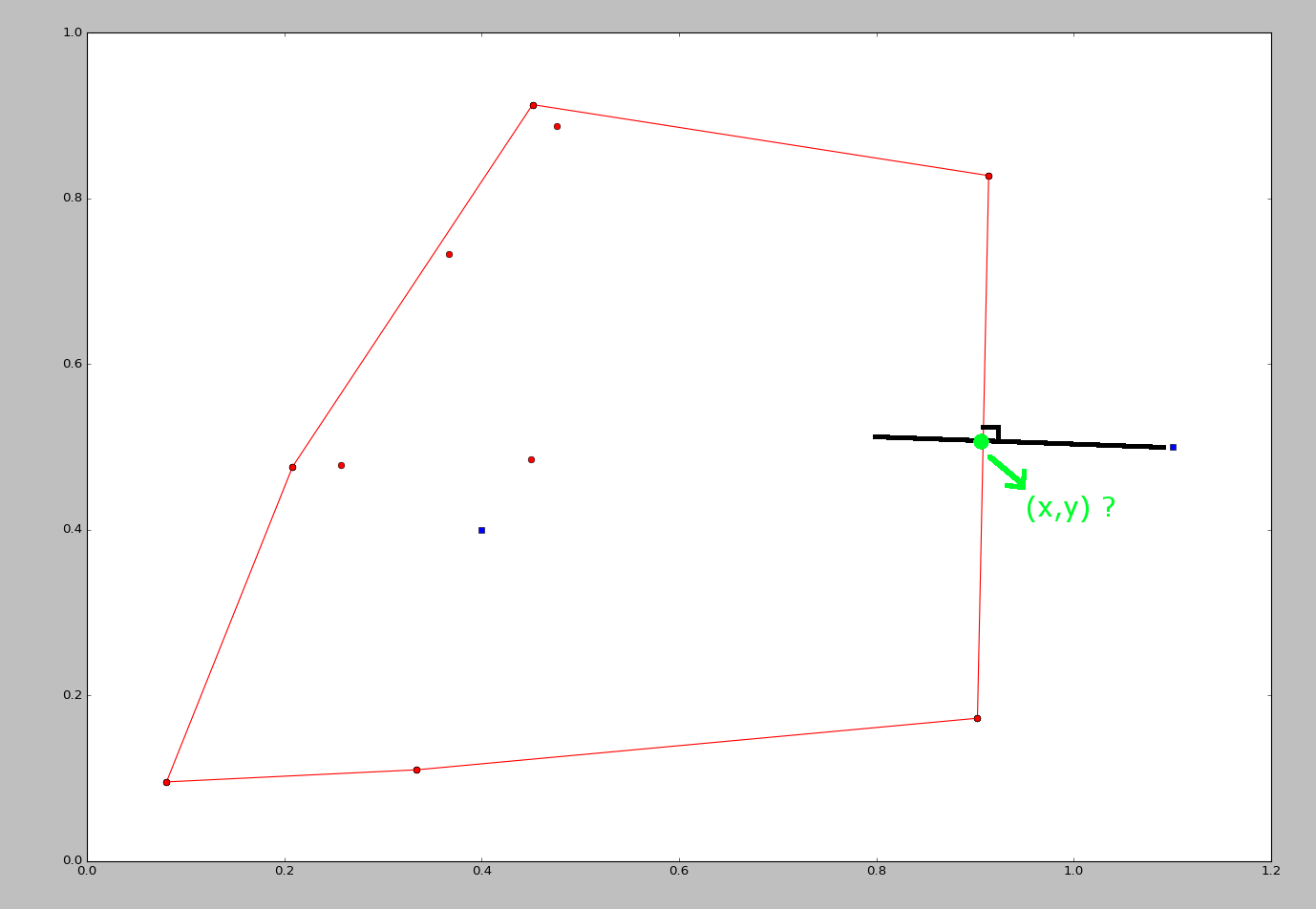
Найти проекцию точки на выпуклую оболочку с помощью Сципи

Question

Из набора точек я получаю выпуклый корпус с scipy.spatialлибо с Delaunay или же ConvexHull (из библиотеки qhull). Теперь я хотел бы получить проекцию точки вне этой выпуклой оболочки на корпус (то есть точку на корпусе, которая является наименьшим расстоянием от точки снаружи).

Это код, который я до сих пор:

from scipy.spatial import Delaunay, ConvexHull
import numpy as np

hu = np.random.rand(10, 2) ## the set of points to get the hull from
pt = np.array([1.1, 0.5]) ## a point outside
pt2 = np.array([0.4, 0.4]) ## a point inside
hull = ConvexHull(hu) ## get only the convex hull
#hull2 = Delaunay(hu) ## or get the full Delaunay triangulation

import matplotlib.pyplot as plt
plt.plot(hu[:,0], hu[:,1], "ro") ## plot all points
#plt.triplot(hu[:,0], hu[:,1], hull2.simplices.copy()) ## plot the Delaunay triangulation
## Plot the convexhull
for simplex in hull.simplices:
    plt.plot(hu[simplex,0], hu[simplex,1], "ro-")

## Plot the points inside and outside the convex hull 
plt.plot(pt[0], pt[1], "bs")
plt.plot(pt2[0], pt2[1], "bs")
plt.show()

С изображением это может быть проще, я хотел бы получить координаты x и y зеленого цвета из синей точки вне выпуклой оболочки. Пример 2d, но мне нужно будет применить его и в более высоком измерении. Спасибо за помощь.

РЕДАКТИРОВАТЬ: проблема решается здесь, но у меня есть проблемы с ее реализацией: https://mathoverflow.net/questions/118088/projection-of-a-point-to-a-convex-hull-in-d-dimensions

Answer 1

Я отвечаю про себя. Как отметил 0Tech, ConvexHull.equations дает уравнения плоскости для каждой плоскости (в 2d --- поэтому линия) в форме: [A, B, C], Таким образом, плоскость определяется

A*x + B*y + C = 0

Проецирование точки P=(x0, y0) на плоскость объясняется здесь: http://www.nabla.hr/CG-LinesPlanesIn3DB5.htm. Требуется точка на векторе, параллельном вектору плоскости (A, B) и проходящая через точку к проекту P, эта линия параметризована как t:

P_proj = (x, y) = (x0 + A*t, y0 + B*t)

Затем вы хотите, чтобы ваша точка находилась на плоскости, и для этого используете полное уравнение плоскости:

A*(x0 + A*t) + B*(y0 + B*t) + C = 0
=> t=-(C + A*x0 + B*y0)/(A**2+B**2)

В (неуклюжем) питоне он дает для любого измерения:

from scipy.spatial import Delaunay, ConvexHull
import numpy as np

hu = np.random.rand(10, 2) ## the set of points to get the hull from
pt = np.array([1.1, 0.5]) ## a point outside
pt2 = np.array([0.4, 0.4]) ## a point inside
hull = ConvexHull(hu) ## get only the convex hull
#hull2 = Delaunay(hu) ## or get the full Delaunay triangulation

import matplotlib.pyplot as plt
plt.plot(hu[:,0], hu[:,1], "ro") ## plot all points
#plt.triplot(hu[:,0], hu[:,1], hull2.simplices.copy()) ## plot the Delaunay triangulation
## Plot the convexhull
for simplex in hull.simplices:
    plt.plot(hu[simplex,0], hu[simplex,1], "ro-")

## Plot the points inside and outside the convex hull 
plt.plot(pt[0], pt[1], "bs")
plt.plot(pt2[0], pt2[1], "bs")

for eq in hull.equations:
    t = -(eq[-1] + np.dot(eq[:-1], pt))/(np.sum(eq[:-1]**2))
    pt_proj = pt + eq[:-1]*t
    plt.plot(pt_proj[0], pt_proj[1], "gD-.")
plt.show()

---

Просмотр stackru привел меня к другому решению, которое имеет преимущество в использовании сегментов вместо линий, поэтому проекция на один из сегментов всегда лежит на сегменте:

def min_distance(pt1, pt2, p):
    """ return the projection of point p (and the distance) on the closest edge formed by the two points pt1 and pt2"""
    l = np.sum((pt2-pt1)**2) ## compute the squared distance between the 2 vertices
    t = np.max([0., np.min([1., np.dot(p-pt1, pt2-pt1) /l])]) # I let the answer of question 849211 explains this
    proj = pt1 + t*(pt2-pt1) ## project the point
    return proj, np.sum((proj-p)**2) ## return the projection and the point

Затем мы можем просмотреть каждую вершину и спроецировать точку:

for i in range(len(hull.vertices)):
    pt_proj, d = min_distance(hu[hull.vertices[i]], hu[hull.vertices[(i+1)%len(hull.vertices)]], pt)
    plt.plot([pt[0], pt_proj[0]], [pt[1], pt_proj[1]], "c<:")

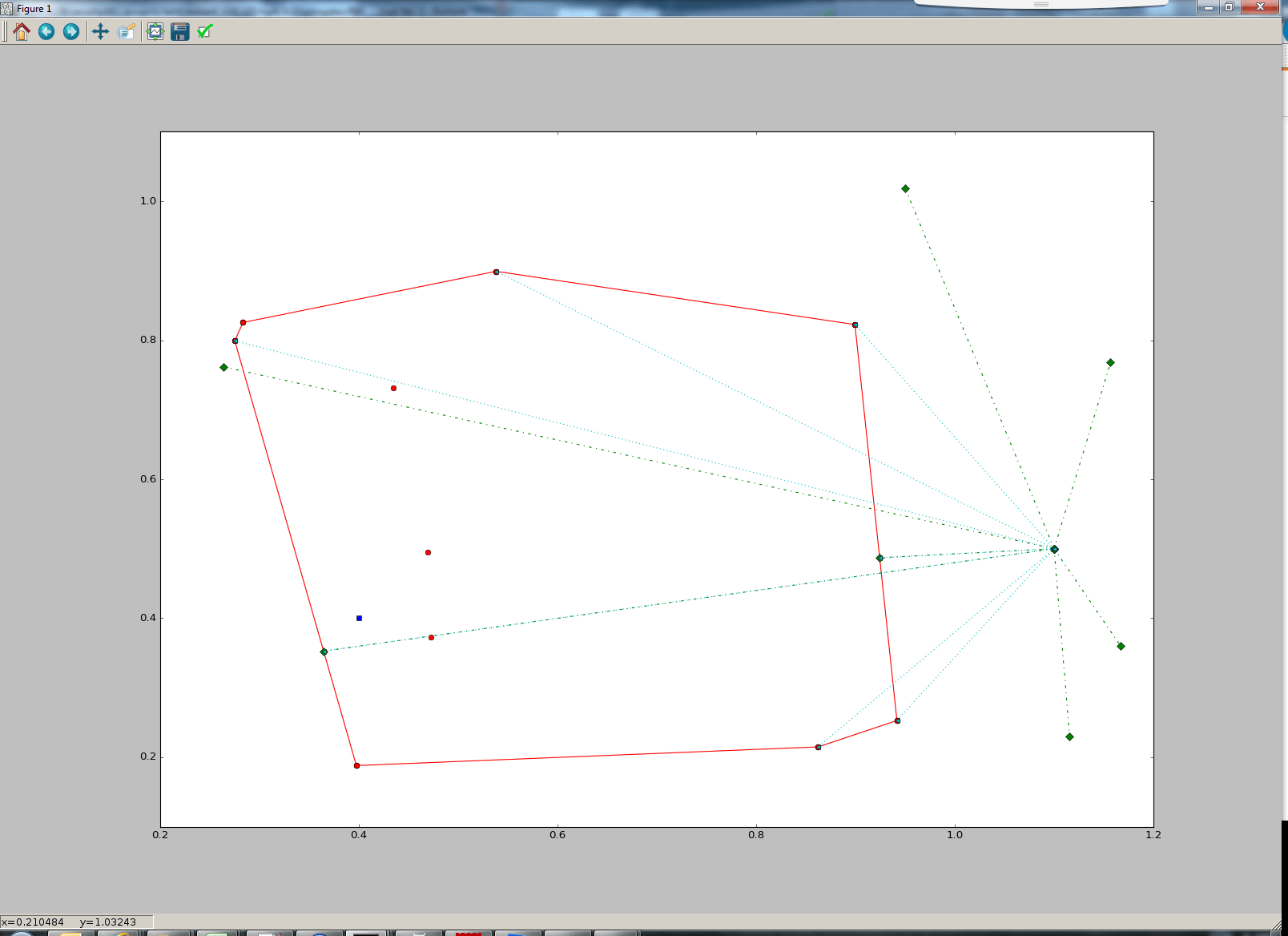
И картинка с проекцией синей точки справа на каждую плоскость (линию) зеленого цвета для первого метода и голубого цвета для второго метода:

Answer 2

Поскольку здесь (или где-либо еще) нет хорошего ответа, я подписался на этот пост (среди прочего) и решил проблему с помощью квадратичного программирования:

$$ \begin{align}\text{minimize} & \quad \frac{1}{2} x^{T} \mathbf{I} x - z^{T} x\\ \text{subject to} & \quad C x \leq b\\ \end{align} $$

где $C$ - нормальные уравнения и $b$это смещения. Ключевое отличие здесь в том, что я проецирую точки внутрь выпуклой оболочки, а не обязательно на нее. т.е. точка внутри выпуклой оболочки останется неизменной, а точки вне выпуклой оболочки будут проецироваться в ближайшую точку выпуклой оболочки (которая всегда будет на ее поверхности). Удалив это ограничение равенства, я получу относительно простую задачу квадратичного программирования, которую я решаю с помощьюquadprog пакет.

Теоретически может существовать более быстрый способ сделать это, но этот способ достаточно быстрый, простой и надежный:

import numpy as np
from scipy.spatial import ConvexHull
from quadprog import solve_qp

def proj2hull(z, equations):
    """
    Project `z` to the convex hull defined by the
    hyperplane equations of the facets

    Arguments
        z: array, shape (ndim,)
        equations: array shape (nfacets, ndim + 1)

    Returns
        x: array, shape (ndim,)
    """
    G = np.eye(len(z), dtype=float)
    a = np.array(z, dtype=float)
    C = np.array(-equations[:, :-1], dtype=float)
    b = np.array(equations[:, -1], dtype=float)
    x, f, xu, itr, lag, act = solve_qp(G, a, C.T, b, meq=0, factorized=True)
    return x

Простой пример:

X = np.random.normal(size=(1000, 5))
z = np.random.normal(scale=2, size=(5))
hull = ConvexHull(X)
y = proj2hull(z, hull.equations)

(Изменить: извините, что не похоже, что латекс форматируется)