"Центр масс" между набором точек на карте с тороидальной оболочкой, которая минимизирует среднее расстояние до всех точек
Как я уже говорил, я ищу точку, минимизирующую общее геодезическое расстояние между всеми остальными точками.
Моя карта топографически похожа на карты в Pac Man и Asteroids. Пройдя мимо вершины, вы перевернетесь на дно, а пройдя мимо слева, вы переместитесь вправо.
Скажем, у меня есть две точки (одинаковой массы) на карте, и я хотел найти их центр масс. Я мог бы использовать классическое определение, которое в основном является серединой.
Однако, скажем, две точки находятся на противоположных концах массы. Существует, так сказать, еще один центр масс, образованный обтеканием "вокруг". По сути, это точка, равноудаленная от обеих других точек, но связанная "обтеканием" края.
пример
b . O . . a . . O .
Две точки O, Их "классическая" середина / центр масс - это точка, обозначенная a, Тем не менее, другая середина также находится на b (b равноудалено от обеих точек, обтекание).
В моей ситуации я хочу выбрать тот, у которого среднее расстояние между двумя точками меньше. В этом случае, a имеет среднее расстояние между двумя точками трех шагов. b имеет среднее расстояние двух шагов. Так что я бы выбрал b,
Один из способов решения ситуации с двумя точками состоит в том, чтобы просто протестировать как классическую среднюю точку, так и самую короткую перевернутую среднюю точку, и использовать ту, которая имеет более короткое среднее расстояние.
Тем не мение! Это нелегко обобщить на 3 балла, или 4, или 5, или n баллов.
Есть ли формула или алгоритм, который я мог бы использовать, чтобы найти это?
(Предположим, что все точки всегда будут иметь одинаковую массу. Я использую только "центр масс", потому что это единственный термин, который я знал, чтобы свободно описать то, что я пытался сделать)
Если мое объяснение неясно, я постараюсь объяснить это лучше.
4 ответа
Понятие центра масс является понятием, относящимся к аффинным пространствам. N-мерный тор не имеет аффинной структуры.
То, что вы хотите, это точка, которая минимизирует (геодезическое) расстояние до всех остальных точек.
Я предлагаю следующее: пусть x_1...x_n будет набором точек на d-мерном торе (или любом другом метрическом пространстве для этой цели).
Твоя проблема:
найти точку mu такую, что сумма (dist(mu, x_k)^2) минимальна.
В аффинно-евклидовом случае вы получаете обычное представление о центре масс.
Это проблема, которую вы сможете решить (например, возможно, есть лучшие варианты) с помощью алгоритма сопряженного градиента, который хорошо работает в этом случае. Помните, что вам нужно умеренное n (скажем, n < 10^3), поскольку алгоритму нужно n^2 в пространстве и n^3 во времени.
Возможно, лучше подходит алгоритм Левенберга-Марквардта, который предназначен для минимизации суммы квадратов.
Обратите внимание, что если у вас есть хорошее начальное предположение (например, обычный центр масс точек, рассматриваемых как точки в R^d вместо тора), метод будет сходиться быстрее.
Изменить: Если (x1...xd) и (y1...yd) являются точками на торе, расстояние задается как dist(x, y)^2 = alpha1^2 + ... + alphad^2
где alphai = min((xi - yi) mod 1, (yi - xi) mod 1)
Я сделал небольшую программу для проверки работоспособности задействованных функций и обнаружил, что вы должны быть очень осторожны с процессом минимизации.
Ниже вы можете увидеть два набора графиков, показывающих распределение точек, функцию минимизации в евклидовом случае и функцию, соответствующую "торической метрике".
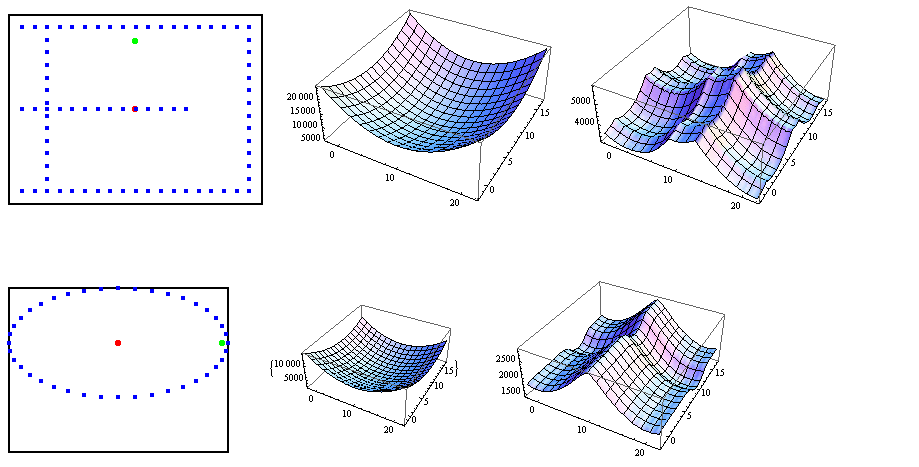
Как вы можете видеть, евклидово расстояние очень хорошо себя ведет, в то время как торик представляет несколько локальных минимумов, которые затрудняют поиск глобальных минимумов. Кроме того, глобальный минимум в торическом случае не является уникальным.
На всякий случай программа в Mathematica это:
Clear["Global`*"];
(*Define non wrapping distance for dimension n*)
nwd[p1_, p2_, n_] := (p1[[n]] - p2[[n]])^2;
(*Define wrapping distance for dimension n *)
wd[p1_, p2_, max_,n_] := (max[[n]] - Max[p1[[n]], p2[[n]]] + Min[p1[[n]], p2[[n]]])^2;
(*Define minimal distance*)
dist[p1_, p2_, max_] :=
Min[nwd[p1, p2, 1], wd[p1, p2, max, 1]] +
Min[nwd[p1, p2, 2], wd[p1, p2, max, 2]];
(*Define Euclidean distance*)
euclDist[p1_, p2_, max_] := nwd[p1, p2, 1] + nwd[p1, p2, 2];
(*Set torus dimensions *)
MaxX = 20;
MaxY = 15;
(*Examples of Points sets *)
lCircle =
Table[{10 Cos[fi] + 10, 5 Sin[fi] + 10}, {fi, 0, 2 Pi - .0001, Pi/20}];
lRect = Join[
Table[{3, y}, {y, MaxY - 1}],
Table[{MaxX - 1, y}, {y, MaxY - 1}],
Table[{x, MaxY/2}, {x, MaxY - 1}],
Table[{x, MaxY - 1}, {x, MaxX - 1}],
Table[{x, 1}, {x, MaxX - 1}]];
(*Find Euclidean Center of mass *)
feucl = FindMinimum[{Total[
euclDist[#, {a, b}, {MaxX, MaxY}] & /@ lRect], 0 <= a <= MaxX,
0 <= b <= MaxY}, {{a, 10}, {b, 10}}]
(*Find Toric Center of mass *)
ftoric = FindMinimum[{Total[dist[#, {a, b}, {MaxX, MaxY}] & /@ lRect],
0 <= a <= MaxX, 0 <= b <= MaxY}, {{a, 10}, {b, 10}}]
В одномерном случае ваша задача будет аналогична поиску среднего угла. Среднее значение углов a и b может быть вычислено как
среднее = остаток ( a + остаток (ba, C)/2,0, C) где C - это мера целого круга (т.е. 2*PI, если вы используете радианы).
Если у вас есть n углов a[], среднее значение может быть вычислено как
среднее = а [0]; для i=1..n среднее = остаток (среднее + остаток ( a[i]-средство, C)/(i+1), C)
Поэтому я считаю,
meanX = X[0]; среднее Y = Y[0]
для я = 1..n
meanX = remainder( meanX + remainder( X[i]-meanX, W)/(i+1), W)
meanY = remainder( meanY + remainder( Y[i]-meanY, H)/(i+1), H)
может сделать работу.
Но обратите внимание, что это приведет к -W/2<=meanX
IANATopologist, и я не знаю, насколько ясно я высказываюсь в этом, но для чего это стоит, вот некоторые мысли по этому вопросу:
Использование массы и гравитации для вычисления такого рода вещей действительно может быть элегантным - ISTR, что существует множество библиотек и эффективных алгоритмов для нахождения векторов гравитации для любого количества масс.
Если бы вы использовали сферическую карту, я бы посоветовал найти внутри сферы фактический центр тяжести для ваших N точек массы. Затем вы проводите линию от центра наружу через этот внутренний центр тяжести, чтобы найти точку на поверхности сферы, где собираются ваши точки массы.
Однако тороидальная карта делает это трудным.
Поэтому я предлагаю выровнять и скопировать вашу карту, чтобы получить 3 × 3 стеганых карт (использование бесконечного поля карт даст лучшие результаты, но может быть излишним). Я назначу им координаты (0, 0) (2, 2), при этом (1, 1) будет вашей исходной картой. Найдите точку (точки), к которой притягиваются точки массы вашей внутренней карты (1, 1) - если они все движутся к середине вашей карты, хорошо: вы нашли свой центр тяжести. Если нет, если одна из точек, расположенных ближе к краю, движется к некоторому накоплению массы за пределами вашей внутренней карты, скажем, в карту (2, 1), то отбросьте эту точку массы при расчете вашего центра тяжести. Вместо этого вы используете точку массы с противоположной карты (в данном случае (0, 1)), которая хочет забраться на вашу среднюю карту.
Добавление векторов ускорения для этих точек массы дает вам центр тяжести на торе. Готово.