Использование повышения точности с тригонометрической функцией
Рассмотрим следующий код, который создает мультиточное число с плавающей точкой "a" с помощью boost.
Как использовать библиотеку Boost для вызова тригонометрических функций? Например, я надеюсь вычислить грех (а).
#include <iostream>
#include "boost/multiprecision/cpp_bin_float.hpp"
using namespace std;
using namespace boost::multiprecision;
typedef number<backends::cpp_bin_float<24, backends::digit_base_2, void, boost::int16_t, -126, 127>, et_off> float32;
int main (void) {
float32 a("0.5");
return 0;
}
2 ответа
Похоже, что в библиотеке есть ограничение. Когда точность падает слишком низко, sin реализация больше не компилируется.
Некоторые промежуточные расчеты проводятся в double точность. Назначение в типе результата будет с потерями и, следовательно, не компилируется.
Ваш выбранный тип на самом деле соответствует cpp_bin_float_single, Это не компилируется.
Как только вы выберете cpp_bin_float_double (точность 53 двоичных разряда) или выше, все будет в порядке.
Я полагаю, что это ограничение можно рассматривать как ошибку в некоторых отношениях. Вы можете сообщить об этом разработчикам библиотеки, которые смогут судить, может ли связанный код использовать плавающие с одинарной точностью, не нарушая сходимости sin приближение.
#include <boost/multiprecision/cpp_bin_float.hpp>
#include <iostream>
using namespace std;
using namespace boost::multiprecision;
int main() {
cpp_bin_float_100 a = 1;
cout << setprecision(50) << endl;
cout << sin(a) << endl;
return 0;
}
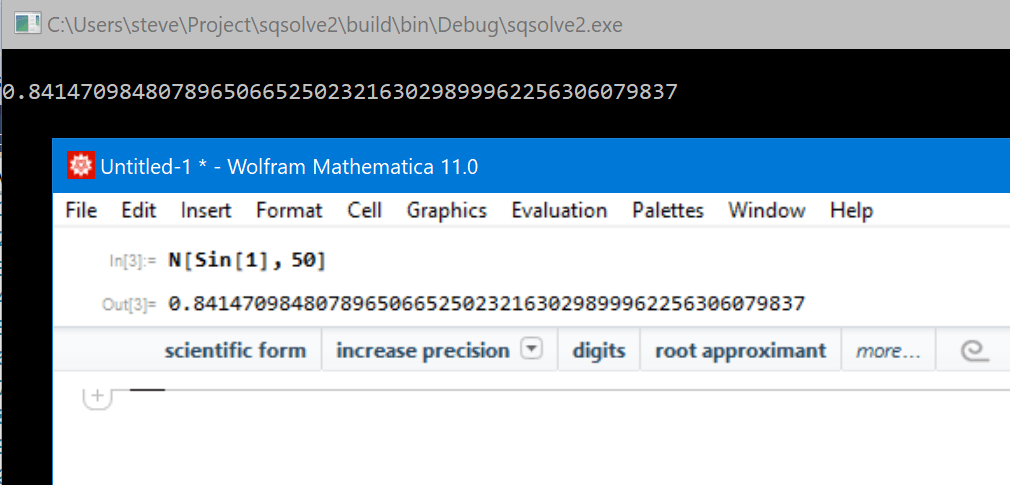
Я сверил цифры с Wolfram Mathematica, и они верны: