Создание K-карт с S2, S1, S0 (семь состояний), одним входом кнопки и четырьмя выходами
Моя диаграмма состояний имеет семь состояний (от 000 до 110), кнопку входа B и четыре выхода P, Q, R и S.
Я сделал таблицу истинности, которая имеет 16 строк (две из которых имеют X). Я должен сделать из этого 7 K-карт, S2' S1' S0' P Q R и S. Я понимаю, что вход B (0, 1) будет на стороне столбца (или строки), но я возникли проблемы с рядами. S2 - наиболее значимая цифра, S0 - наименее.
Я никогда не видел K-карту с 3-мя битами (S2/S1/S0) на одной стороне, но я не знаю, как представить ее любым другим способом. И если это три бита, в каком порядке идут эти числа? Для двоих я знаю, что это 00/01/11/10.
Если это два, что кажется правильной идеей, то как вы выбираете между двумя из трех (S2/S1/S0)? Получает ли сторона ввода B дополнительную переменную рядом с ней (так что это будет S2 / S1 в столбце и B/S0 в строках?). Как вы решаете, какой из S2 / S1 / S0 находится на другой стороне, имеет ли это значение?
Одна большая помощь для меня - увидеть пример таблицы истинности /k-карт для диаграммы состояний S2 / S1 / S0. Я только когда-либо видел примеры S1 / S0, так что не более 4 штатов (00/01/10/11).
Спасибо за любую помощь, которую вы можете предоставить. Извините, если мой вопрос сбивает с толку. Пожалуйста, дайте мне знать, если я могу быть более ясным о моей проблеме.
1 ответ
Сначала есть ответы на ваши вопросы:
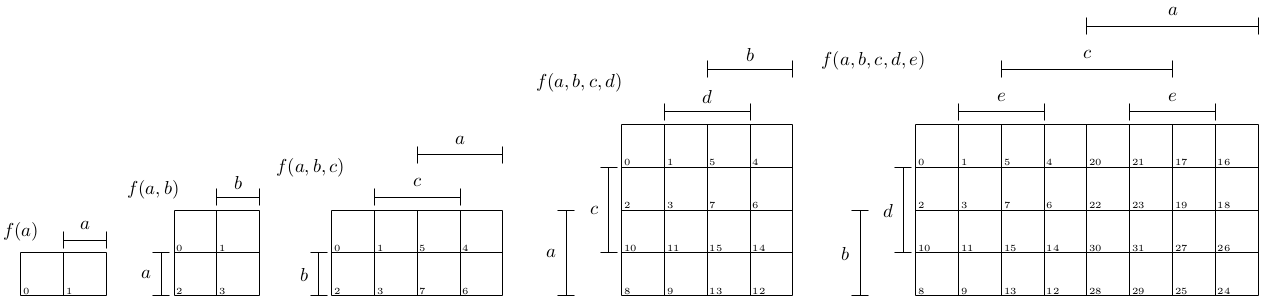
Количество ячеек на каждой карте Карно соответствует количеству всех возможных входных комбинаций. Способ индексации ячеек карты должен соответствовать таблице истинности. На следующем рисунке приведены примеры карт Карно разных размеров, где визуализация соседних ячеек все еще довольно проста.
Как видите, дело в том, что две соседние ячейки отличаются только значением одной переменной, четыре соседние ячейки отличаются значениями двух переменных и так далее. Вот почему вы должны искать группы, которые имеют размер 2^n. Индексирование карты может выглядеть немного запутанным, но это делается для того, чтобы показать все отношения между каждой строкой в таблице истинности.
Если вы индексируете K-карту, но не знаете, какие строки для каких переменных и в каком порядке они должны указывать, то вы можете проверить это следующим образом:
- индекс 0 = где ни одна переменная не является истинной
- индекс 1 = где только младший значащий бит является истинным (для таблицы истинности, упорядоченной abcd, которая будет d)
- index 2 =, где только второй младший значащий бит является истинным (для той же таблицы истинности, которая была бы c)
- индекс 4 = где только третий младший значащий бит является истинным (для той же таблицы истинности, которая будет b)
- индекс 8 = где только четвертый младший значащий бит является истинным (для той же таблицы истинности, которая будет a)
Как для примера: здесь вы можете увидеть диаграмму состояний генератора последовательностей 01364, реализованного как машина Мура. Все ребра машины обозначены входным значением кнопки сброса.
Желаемое поведение машины и выходные значения, соответствующие состояниям, могут быть описаны этой таблицей переходов:
state || output (decimal) | reset || next state
-------------------------------------------------
S_0 || 0 | 0 || S_1
|| | 1 || S_0
-------------------------------------------------
S_1 || 1 | 0 || S_2
|| | 1 || S_0
-------------------------------------------------
S_2 || 3 | 0 || S_3
|| | 1 || S_0
-------------------------------------------------
S_3 || 6 | 0 || S_4
|| | 1 || S_0
-------------------------------------------------
S_4 || 4 | 0 || S_0
|| | 1 || S_0
После кодирования представления состояний для соответствия десятичных выходных данных в двоичном формате (q_2, q_1 и q_0; d_2, d_1 и d_0) таблица перехода выглядит следующим образом:
state || q_2 | q_1 | q_0 | reset || d_2 | d_1 | d_0 || next state
-------------------------------------------------------------------
S_0 || 0 | 0 | 0 | 0 || 0 | 0 | 1 || S_1
|| | | | 1 || 0 | 0 | 0 || S_0
-------------------------------------------------------------------
S_1 || 0 | 0 | 1 | 0 || 0 | 1 | 1 || S_2
|| | | | 1 || 0 | 0 | 0 || S_0
-------------------------------------------------------------------
S_2 || 0 | 1 | 1 | 0 || 1 | 1 | 0 || S_3
|| | | | 1 || 0 | 0 | 0 || S_0
-------------------------------------------------------------------
S_3 || 1 | 1 | 0 | 0 || 1 | 0 | 0 || S_4
|| | | | 1 || 0 | 0 | 0 || S_0
-------------------------------------------------------------------
S_4 || 1 | 0 | 0 | 0 || 0 | 0 | 0 || S_0
|| | | | 1 || 0 | 0 | 0 || S_0
Полезно изучить таблицу переходов для каждой возможной комбинации входных данных, потому что есть некоторые выходные значения 'все равно' (x) (для состояний, которых нет в последовательности), которые можно использовать для минимизации с помощью Карно карты.
index | state || q_2 | q_1 | q_0 | reset || d_2 | d_1 | d_0 || next state
---------------------------------------------------------------------------
0 | S_0 || 0 | 0 | 0 | 0 || 0 | 0 | 1 || S_1
1 | S_0 || 0 | 0 | 0 | 1 || 0 | 0 | 0 || S_0
---------------------------------------------------------------------------
2 | S_1 || 0 | 0 | 1 | 0 || 0 | 1 | 1 || S_2
3 | S_1 || 0 | 0 | 1 | 1 || 0 | 0 | 0 || S_0
---------------------------------------------------------------------------
4 | - || 0 | 1 | 0 | 0 || x | x | x || -
5 | - || 0 | 1 | 0 | 1 || 0 | 0 | 0 || S_0
---------------------------------------------------------------------------
6 | S_2 || 0 | 1 | 1 | 0 || 1 | 1 | 0 || S_3
7 | S_2 || 0 | 1 | 1 | 1 || 0 | 0 | 0 || S_0
---------------------------------------------------------------------------
8 | S_4 || 1 | 0 | 0 | 0 || 0 | 0 | 0 || S_0
9 | S_4 || 1 | 0 | 0 | 1 || 0 | 0 | 0 || S_0
---------------------------------------------------------------------------
10 | - || 1 | 0 | 1 | 0 || x | x | x || -
11 | - || 1 | 0 | 1 | 1 || 0 | 0 | 0 || S_0
---------------------------------------------------------------------------
12 | S_3 || 1 | 1 | 0 | 0 || 1 | 0 | 0 || S_4
13 | S_3 || 1 | 1 | 0 | 1 || 0 | 0 | 0 || S_0
---------------------------------------------------------------------------
14 | - || 1 | 1 | 1 | 0 || x | x | x || -
15 | - || 1 | 1 | 1 | 1 || 0 | 0 | 0 || S_0
Наконец, вы можете видеть, что функции, определяющие d_2, d_1 и d_0 (то есть двоичное кодированное состояние / выход, соответствующий номеру в последовательности 01364), могут быть просто выделены в следующих K-картах.
f(d_2) = q_1 ⋅ ¬(reset)
f(d_1) = q_0 ⋅ ¬(reset)
f(d_0) = ¬(q_2) ⋅ ¬(q_1) ⋅ ¬(reset)
(Все изображения были созданы с использованием латекса.)