Маленькая интрижка только для вечеринок *&co
Я с трудом понимаю, что происходит с The Little Schemer's evens-only*&co пример на стр. 145.
Вот код:
(define evens-only*&co
(lambda (l col)
(cond
((null? l)
(col '() 1 0))
((atom? (car l))
(cond
((even? (car l))
(evens-only*&co (cdr l)
(lambda (newl product sum)
(col (cons (car l) newl)
(opx (car l) product)
sum))))
(else
(evens-only*&co (cdr l)
(lambda (newl product sum)
(col newl product (op+ (car l) sum)))))))
(else
(evens-only*&co (car l)
(lambda (newl product sum)
(evens-only*&co (cdr l)
(lambda (dnewl dproduct dsum)
(col (cons newl dnewl)
(opx product dproduct)
(op+ sum dsum))))))))))
Начальный col может быть:
(define evens-results
(lambda (newl product sum)
(cons sum (cons product newl))))
То, что я не получаю, это с l как '((1) 2 3)Сразу же идет в финал else с (car l) как (1) а также (cdr l) как (2 3), Хорошо, но мой разум сходит с ума, пытаясь разобраться dnewl, dproduct, dsum от newl, product, sum, Также было бы полезно, если бы кто-нибудь мог научить меня, как настроить DrRacket, Chez Scheme или MIT-Scheme для запуска степпера.
Но, может быть, я спазмирую слишком рано. Любой начинающий, читающий это впервые, должен понимать это дикое продолжение?
4 ответа
Я нашел этот раздел запутывающим и при первом чтении, и начал понимать его только после того, как прочитал в другом месте о продолжениях и стиле прохождения продолжения (что и есть).
С риском объяснения чего-то, что вы уже получили, один из способов взглянуть на это, который помог мне, состоит в том, чтобы думать о "сборщике" или "продолжении" как о замене обычного способа, которым функция возвращает значения. В обычном стиле программирования вы вызываете функцию, получаете значение и что-то делаете с ним в вызывающей программе. Например, стандартная рекурсивная length функция включает в себя выражение (+ 1 (length (cdr list))) для непустого случая. Это означает, что когда-то (length (cdr list)) возвращает значение, есть вычисление, ожидающее выполнения с любым значением, которое оно производит, которое мы могли бы представить как (+ 1 [returned value]), В обычном программировании интерпретатор отслеживает эти ожидающие вычисления, которые имеют тенденцию "складываться", как вы можете видеть в первых нескольких главах книги. Например, при рекурсивном вычислении длины списка мы имеем гнездо "ожидающих вычислений" на столько уровней, сколько длина списка длинна.
В стиле прохождения продолжения вместо вызова функции и использования возвращаемого результата в вызывающей функции мы сообщаем функции, что делать, когда она выдает свое значение, предоставляя ей "продолжение" для вызова. (Это похоже на то, что вы делаете с обратными вызовами в асинхронном программировании Javascript, например: вместо записи result = someFunction(); ты пишешь someFunction(function (result) { ... })и весь код, который использует result идет внутри функции обратного вызова).
Вот length в стиле продолжения, просто для сравнения. Я назвал параметр продолжения return, который должен подсказать, как он функционирует здесь, но помните, что это обычная переменная Scheme, как и любая другая. (Часто параметр продолжения называется k в этом стиле).
(define (length/k lis return)
(cond ((null? lis) (return 0))
(else
(length/k (cdr lis)
(lambda (cdr-len)
(return (+ cdr-len 1)))))))
Существует полезный совет для прочтения такого рода кода в статье о продолжениях соавтора Little Littlemer Дэна Фридмана. (См. Раздел II-5, начиная со стр. 8). Перефразируя, вот что else пункт выше говорит:
представьте, у вас есть результат вызова
length/kна(cdr lis)и назовите этоcdr-len, затем добавьте один и передайте результат этого дополнения вашему продолжению (return).
Обратите внимание, что это почти то, что переводчик должен делать при оценке (+ 1 (length (cdr lis))) в обычной версии функции (за исключением того, что она не должна давать имя промежуточному результату (length (cdr lis)), Обойдя продолжения или обратные вызовы, мы сделали явный поток управления (и имена промежуточных значений) вместо того, чтобы интерпретатор следил за ним.
Давайте применим этот метод к каждому предложению в evens-only*&co, Это немного усложняется тем фактом, что эта функция выдает три значения, а не одно: вложенный список с удаленными нечетными числами; произведение четных чисел; и сумма нечетных чисел. Вот первый пункт, где (car l) известно, что это четное число:
(evens-only*&co (cdr l)
(lambda (newl product sum)
(col (cons (car l) newl)
(opx (car l) product)
sum)))
Представьте, что у вас есть результаты удаления нечетных чисел, умножения четных чисел и добавления нечетных чисел из
cdrиз списка, и позвоните имnewl,product, а такжеsumсоответственно.consглава списка наnewl(так как это четное число, оно должно идти в результате); умножатьproductпо заголовку списка (так как мы рассчитываем произведение четных чисел); Покидатьsumв одиночестве; и передать эти три значения вашему ожиданию продолженияcol,
Вот случай, когда заголовок списка является нечетным числом:
(evens-only*&co (cdr l)
(lambda (newl product sum)
(col newl product (op+ (car l) sum))))
Как и раньше, но передать те же значения newl а также product к продолжению (т.е. "вернуть" их) вместе с суммой sum и глава списка, так как мы суммируем нечетные числа.
И вот последний, где (car l) это вложенный список, который немного усложняется двойной рекурсией:
(evens-only*&co (car l)
(lambda (newl product sum)
(evens-only*&co (cdr l)
(lambda (dnewl dproduct dsum)
(col (cons newl dnewl)
(opx product dproduct)
(op+ sum dsum))))))
Представьте, что у вас есть результаты удаления, суммирования и добавления чисел в
(car l)и называть этоnewl,product, а такжеsum; затем представьте, что у вас есть результаты от того же(cdr l)и позвони имdnewl,dproductа такжеdsum, В ожидании продолжения укажите значения, полученныеconsИНГnewlа такжеdnewl(так как мы создаем список списков); умножение вместеproductа такжеdproduct; и добавлениеsumа такжеdsum,
Обратите внимание: каждый раз, когда мы делаем рекурсивный вызов, мы создаем новое продолжение рекурсивного вызова, которое "закрывает" текущие значения аргумента, lи обратное продолжение - colдругими словами, вы можете думать о цепочке продолжений, которую мы строим во время рекурсии, как о моделировании "стека вызовов" более условно написанной функции!
Надеюсь, что это даст часть ответа на ваш вопрос. Если я немного переборщил, то только потому, что думал, что после самой рекурсии продолжения - это вторая действительно изящная, расширяющая сознание идея в "Маленьком интрижке" и программировании в целом.
Ответ Jon O.. - действительно большое подробное объяснение основных понятий. Хотя для меня (и, надеюсь, для некоторых других людей), понимание таких понятий намного проще, когда они имеют визуальное представление.
Итак, я подготовил две блок-схемы (похожие на те, которые я сделал дляmultirember&coраспутывая происходящее во время вызова evens-only*&co
дано l является:
'((9 1 2 8) 3 10 ((9 9) 7 6) 2)
а также col является:
(define the-last-friend
(lambda (newl product sum)
(cons sum (cons product newl))
)
)
Одна блок-схема, отражающая взаимосвязь переменных на разных этапах рекурсии: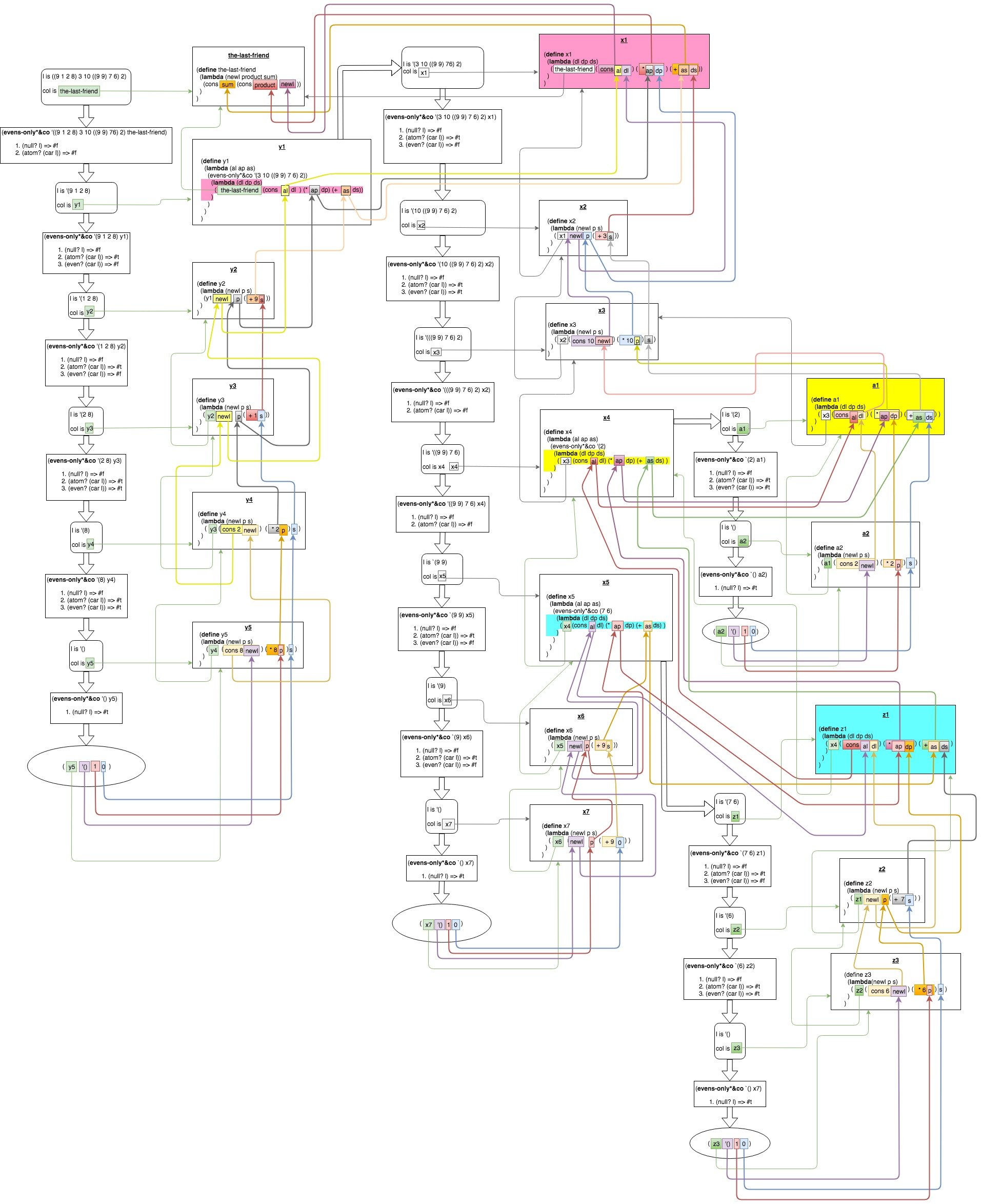 
Вторая блок-схема, показывающая фактические значения, передается: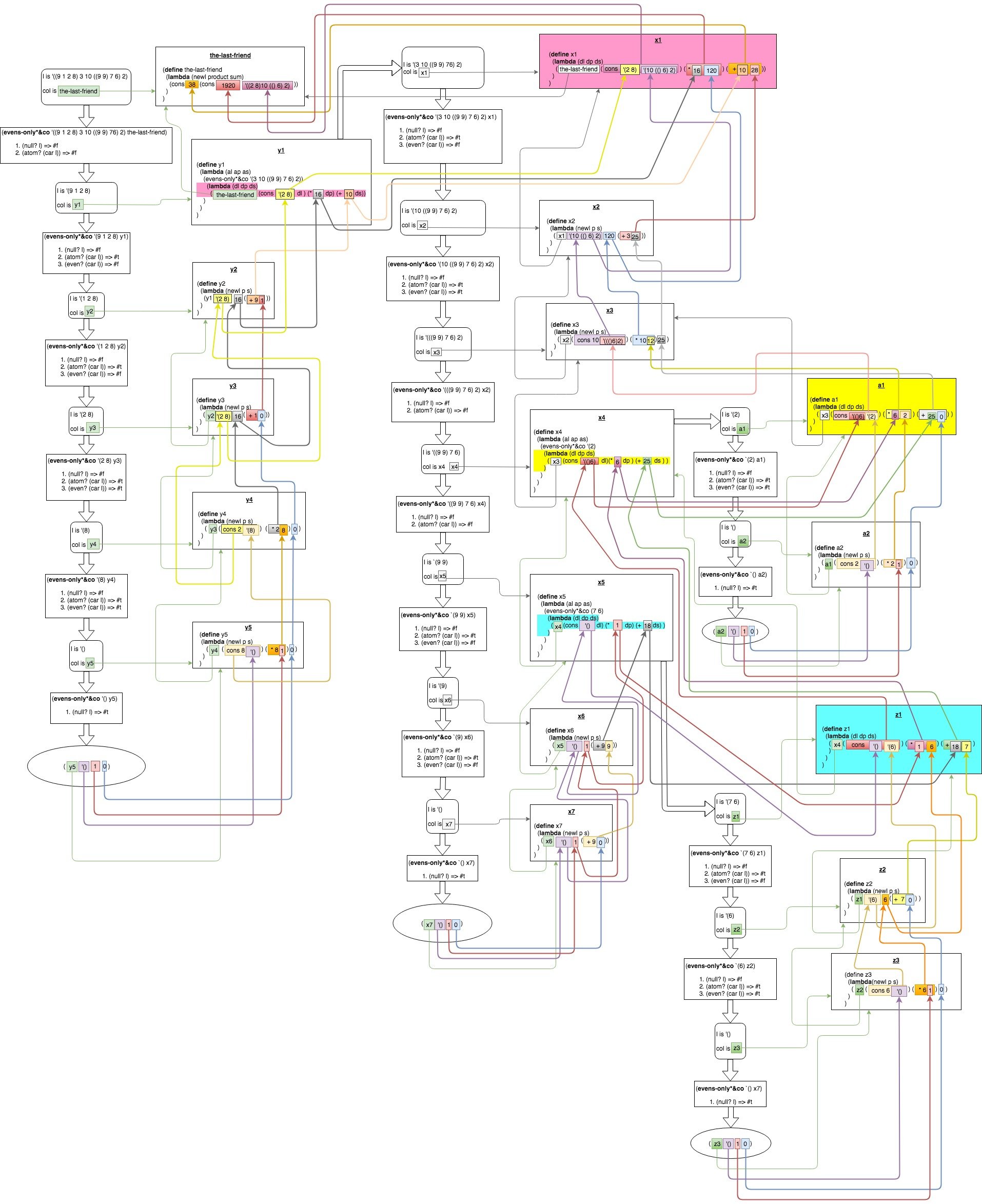 
Я надеюсь, что этот ответ станет достойным дополнением к объяснению Джона выше.
В эквациональном псевдокоде (нотация, подобная KRC, f x y для вызова (f x y) где это однозначно) это
evens-only*&co l col
= col [] 1 0 , IF null? l
= evens-only*&co (cdr l)
( newl product sum =>
col (cons (car l) newl)
(opx (car l) product)
sum ) , IF atom? (car l) && even? (car l)
= evens-only*&co (cdr l)
( newl product sum =>
col newl product (op+ (car l) sum) ) , IF atom? (car l)
= evens-only*&co (car l)
( anewl aproduct asum =>
evens-only*&co (cdr l)
( dnewl dproduct dsum =>
col (cons anewl dnewl)
(opx aproduct dproduct)
(op+ asum dsum) ) ) , OTHERWISE
Это код CPS, который собирает все четные числа из входного вложенного списка (т. Е. Дерева), сохраняя древовидную структуру, а также находит произведение всех четных чисел; что касается нечетных событий, то они суммируют их:
если
lпустой список, три базовых значения (идентификатора) передаются в качестве аргументов в col;если
(car l)четное число, результаты обработки(cdr l)являютсяnewl,productа такжеsumи затем они передаются в качестве аргументовcolв то время как первые два дополняются умножением ⁄ на(car l)(четное число);если
(car l)является атомом, который не является четным числом, результаты обработки(cdr l)являютсяnewl,productа такжеsumи затем они передаются в качестве аргументовcolс третьим дополнен суммированием с(car l)(атом четного числа);если
(car l)список, результаты обработки(car l)являютсяanewl,aproductа такжеasumа затем результаты обработки(cdr l)являютсяdnewl,dproductа такжеdsumи затем три объединенных результата передаются в качестве аргументовcol,
[], 1 а также 0 базового случая - единичные элементы моноидов списков, чисел при умножении и чисел при сложении соответственно. Это просто означает специальные значения, которые не меняют результат при объединении в него.
В качестве иллюстрации для '((5) 2 3 4) (что близко к примеру в вопросе), это создает расчет
evens-only*&co [[5], 2, 3, 4] col
=
col (cons [] ; original structure w only the evens kept in,
(cons 2 ; for the car and the cdr parts
(cons 4 [])))
(opx 1 ; multiply the products of evens in the car and
(opx 2 (opx 4 1))) ; in the cdr parts
(op+ (op+ 5 0) ; sum, for the non-evens
(op+ 3 0))
Подобно моему другому ответу (на вопрос сестры), вот еще один способ написать это, с псевдокодом, соответствующим шаблону (с охранниками):
evens-only*&co = g where
g [a, ...xs...] col
| pair? a = g a ( la pa sa =>
g xs ( ld pd sd =>
col [la, ...ld...] (* pa pd) (+ sa sd) ) )
| even? a = g xs ( l p s => col [ a, ...l... ] (* a p ) s )
| otherwise = g xs ( l p s => col l p (+ a s ) )
g [] col = col [] 1 0
Экономия (и разнообразие) этой нотации действительно делает все это намного более понятным, проще увидеть, вместо того, чтобы заблудиться в словесном наборе длинных имен для функций и переменных, так как парены перегружаются как синтаксические разделители для данных списка, группировок предложений (как в cond выражения), привязки имен (в lambda выражения) и указатели на вызовы функций выглядят совершенно одинаково. Та же однородность обозначений S-выражений, которая способствует простоте манипулирования машиной (например, lisp's read и макросы) - это то, что наносит ущерб читабельности человека.
Я читал, как разрабатывать программы (felleisen et.al.). Я иду через раздел, где они определяют локальные определения. Я написал код, который реализует вышеприведенные четные и совместные с использованием локального определения. Вот что я написал:
(define (evens-only&co l)
(local ((define (processing-func sum prod evlst lst)
(cond ((null? lst) (cons sum (cons prod evlst)))
((atom? (car lst))
(cond ((even? (car lst)) (processing-func sum (* prod (car lst)) (append evlst (list (car lst))) (cdr lst)))
(else
(processing-func (+ sum (car lst)) prod evlst (cdr lst)))))
(else
(local ((define inner-lst (processing-func sum prod '() (car lst))))
(processing-func (car inner-lst) (cadr inner-lst) (append evlst (list (cddr inner-lst))) (cdr lst)))))))
(processing-func 0 1 '() l)))
Для тестирования, когда я ввожу (только по четности и со '((9 1 2 8) 3 10 ((9 9) 7 6) 2)), возвращается "(38 1920 (2 8) 10 (() 6) 2) как и ожидалось в маленьком интриганке. Но мой код не выполняется в одном условии: когда четных чисел нет вообще, произведение четных чисел по-прежнему отображается как 1. Например (только четные &co '((9 1) 3 ((9 9) 7))) возвращает '(38 1 () (())). Я думаю, мне понадобится дополнительная функция, чтобы исправить это. @melwasul: Если вы не знакомы с местным определением, извините, чтобы опубликовать это здесь. Я предлагаю вам прочитать HTDP тоже. Это отличная книга для начинающих. Но ребята, которые являются экспертами в схемах, могут также оставить свои комментарии к моему коду. Правильно ли мое понимание местного определения?