Объясните пример продолжения на стр.137 "Маленького мошенника"

Question

Код в вопросе это:

(define multirember&co
  (lambda (a lat col)
    (cond
     ((null? lat)
      (col (quote ()) (quote ())))
     ((eq? (car lat) a)
      (multirember&co a
                      (cdr lat)
                      (lambda (newlat seen)
                        (col newlat
                             (cons (car lat) seen)))))
     (else
      (multirember&co a
                      (cdr lat)
                      (lambda (newlat seen)
                        (col (cons (car lat) newlat)
                             seen))))))

Я смотрел на это весь день, но я не могу понять это. Когда вы возвращаетесь к функции, вы переопределяете col но в примерах они, кажется, используют оригинальное определение. Почему это не изменится. Как вы можете повторить это, не передавая параметры newlat а также seen,

Трудно объяснить мой вопрос, потому что я, кажется, просто скучаю. Если, возможно, кто-то сможет дать более подробное описание, чем книга, я смогу понять, как это работает.

Answer 1

Давайте рассмотрим пример; возможно это поможет.:-) Для простоты я просто собираюсь использовать list как сборщик / продолжение, которое будет просто возвращать список с аргументами для продолжения.

(multirember&co 'foo '(foo bar) list)

В начале,

a = 'foo
lat = '(foo bar)
col = list

На первой итерации (eq? (car lat) a) условие соответствует, так как lat не пустой, а первый элемент lat является 'foo, Это устанавливает следующую рекурсию к multirember&co Таким образом:

a = 'foo
lat = '(bar)
col = (lambda (newlat seen)
        (list newlat (cons 'foo seen))

На следующей итерации else совпадения: с lat не пустой, а первый элемент lat является 'bar (и не 'foo). Таким образом, для следующей рекурсии мы имеем:

a = 'foo
lat = '()
col = (lambda (newlat seen)
        ((lambda (newlat seen)
           (list newlat (cons 'foo seen)))
         (cons 'bar newlat)
         seen))

Для удобства чтения (и во избежание путаницы) мы можем переименовать параметры (из-за лексической области видимости) без каких-либо изменений в семантике программы:

col = (lambda (newlat1 seen1)
        ((lambda (newlat2 seen2)
           (list newlat2 (cons 'foo seen2)))
         (cons 'bar newlat1)
         seen1))

Наконец, (null? lat) пункт соответствует, так как lat сейчас пусто. Итак, мы называем

(col '() '())

который расширяется до:

((lambda (newlat1 seen1)
   ((lambda (newlat2 seen2)
      (list newlat2 (cons 'foo seen2)))
    (cons 'bar newlat1)
    seen1))
 '() '())

который (при замене newlat1 = '() а также seen1 = '()) становится

((lambda (newlat2 seen2)
   (list newlat2 (cons 'foo seen2)))
 (cons 'bar '())
 '())

или (оценивая (cons 'bar '()))

((lambda (newlat2 seen2)
   (list newlat2 (cons 'foo seen2)))
 '(bar)
 '())

Теперь подставим значения newlat2 = '(bar) а также seen2 = '(), мы получаем

(list '(bar) (cons 'foo '()))

или, другими словами,

(list '(bar) '(foo))

дать наш окончательный результат

'((bar) (foo))

Answer 2

Я нашел замечательный ответ здесь: http://www.michaelharrison.ws/weblog/?p=34

Я тоже боролся с этим. Ключ должен понять лексическую область видимости (для меня, а-ля Javascript) и внутренние функции, переданные multirember & co в ветвях eq, а не eq. Поймите это, и вы поймете всю процедуру.

Answer 3

Я боролся с собой, чтобы понять, что происходит внутри multirember&co, некоторое время. Проблема в том, что в тот момент, когда я думал, что у меня это есть - следующее задание / пример доказал, что у меня нет.

Что помогло мне, так это составить визуальное представление о том, что происходит (для меня текстовые прохождения трудно понять по некоторым причинам).

Итак, я собрал две блок-схемы:

Один, просто показывающий отношения между различными этапами рекурсии:

---

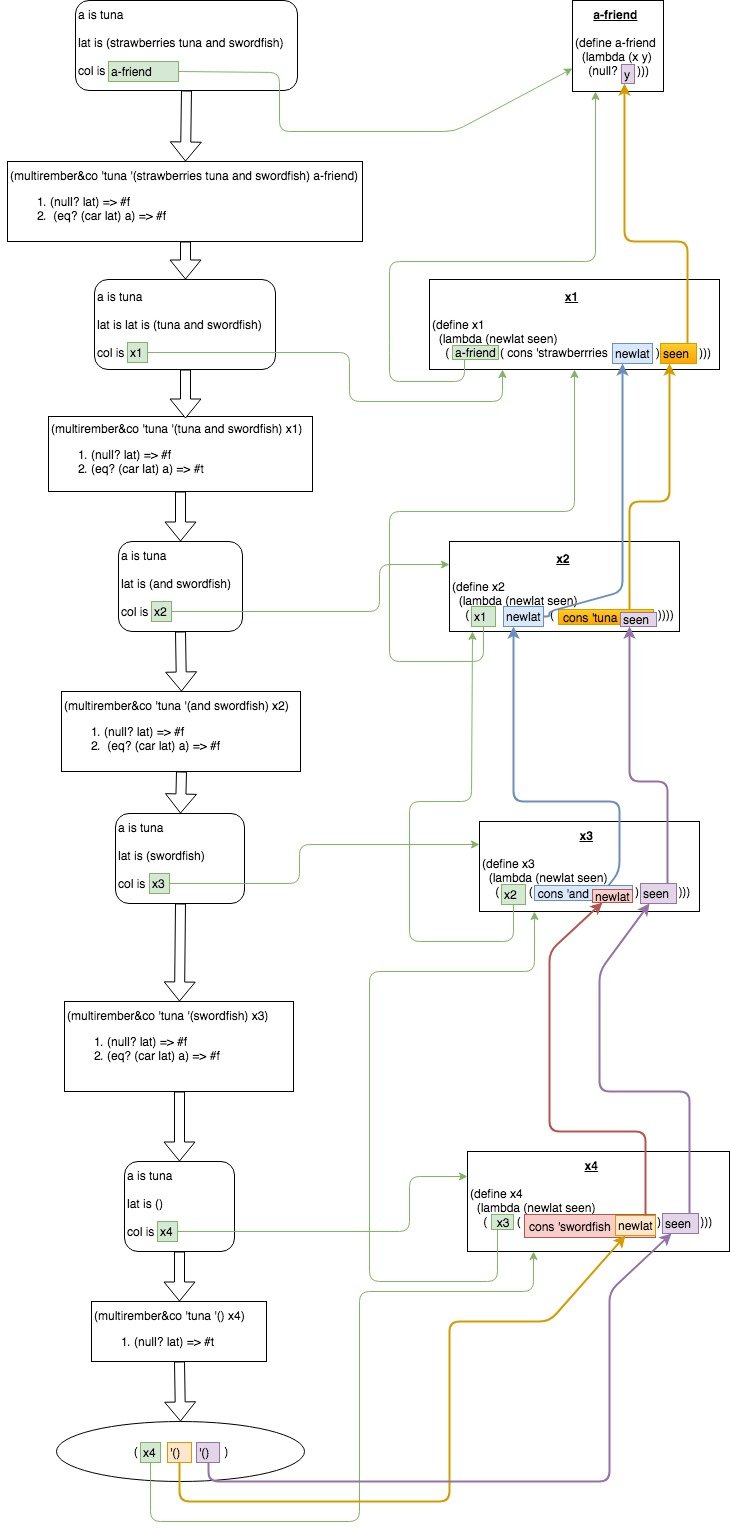
И еще один, отражающий реальные значения:



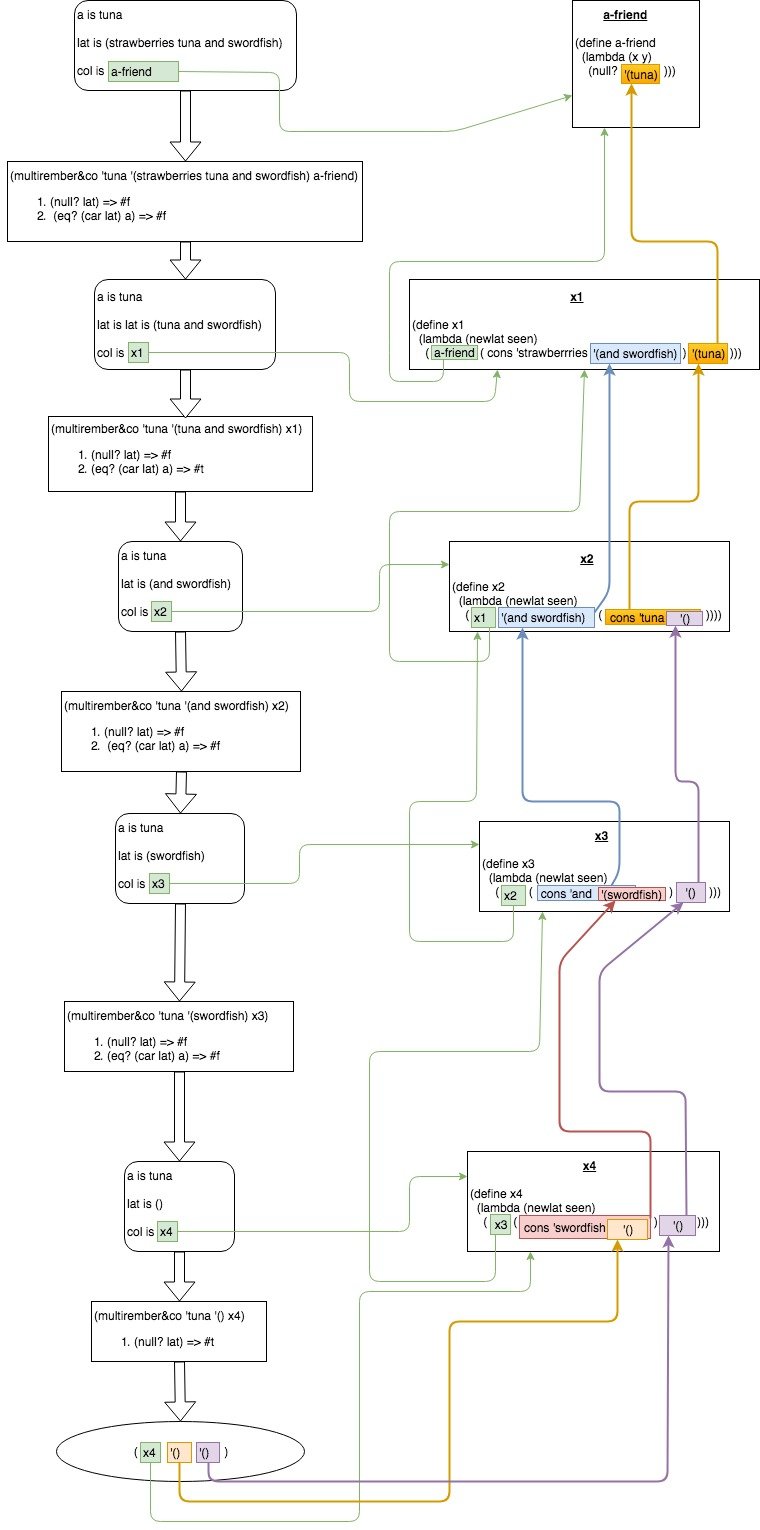
Теперь, когда я чувствую, что снова теряю "нить аргумента", я просто обращаюсь к этим блок-схемам, и они возвращают меня в нужное русло.

Еще одна вещь, которую я понял после просмотра "всей картины" с помощью блок-схемы, это то, что a-friend Функция просто проверяет, seen содержит какие-либо значения или нет (хотя он возвращает его наоборот, т.е. #f когда есть значения в seen а также #t когда seen пусто, что может сбить с толку.

PS: я делал похожие блок-схемы дляevens-only*&co, который появляется позже в книге.

Answer 4

То, что ссылка выше (http://www.michaelharrison.ws/weblog/?p=34) хорошо объясняет, это то, как все это упражнение состоит в том, чтобы избежать необходимости императивного программирования (C, Java) объявлять двух "держателей" или "сборщиков" msgstr "переменные (или списки, векторы) явно в памяти, чтобы поймать ваши ответы при переборе списка. Используя продолжение схемы на языке FP, вы не "проталкиваете" результаты теста, проходя через (земляничный тунец и рыба-меч) в отдельно созданные "корзины"; вместо этого вы объединяете два списка при отправке соответствующих функций - один для eq? правда, другой для эквалайзера? ложь - через рецидивы.,, наконец, заканчивается третьей функцией col, которая в первом примере TLS является "другом", которая спрашивает, пуст ли список, созданный для хранения всех совпадений (нуль?). Затем TLS просит вас "запустить" multirember&co снова с новым "последним" столбцом, который просто запрашивает список, содержащий все атомы "не тунца", сколько в нем содержится ("последний друг"). Таким образом, есть две "первоклассные" функции, используемые для работы с задачей сбора, то есть построения двух отдельных списков, а затем в конце раскручивания рекурсии оригинальный col ("друг") задает последний вопрос. Возможно, имя "multirember & co" не является лучшим именем, потому что оно действительно не перестраивает список минус атом, который будет удален; скорее, он строит два отдельных списка - которые никогда не отображаются - затем применяет последний col (a-friend или last-friend).,, который отображает либо #t или #f, либо длину списка "не тунца".

Вот некоторые результаты:

> (multirember&co 'tuna '(and tuna) a-friend)
#f
> (multirember&co 'tuna '(and not) a-friend)
#t

Вот столбец, чтобы вернуть список несоответствий:

(define list-not  (lambda (x y) x))

и его использование:

> (multirember&co 'tuna '(and not) list-not)
(and not)

Answer 5

Давайте используем эквалайзерный псевдокод с некоторыми скобками, опущенными для ясности (поэтому мы пишем f x y для вызова (f x y)где это однозначно)

multirember&Co a lat col
    = col [] []                                , IF lat == [] 

    = multirember&Co a (cdr lat)
         ( newlat seen => 
             col newlat
                 (cons (car lat) seen) )       , IF (car lat) == a

    = multirember&Co a (cdr lat)
         ( newlat seen => 
             col (cons (car lat) newlat)
                 seen )                        , OTHERWISE

Разве это не самоочевидно, что это делает?:) Еще нет?:) Переписав снова с воображаемым псевдокодом для сопоставления с образцом (с охранниками), мы имеем

multirember&Co = g where
    g a [b, ...lat] col | b == a  =  g a lat ( n s => col     n     [b, ...s] )
                        | else    =  g a lat ( n s => col [b, ...n]     s     )
    g a []          col           =                   col     []        []

Семантика сопоставления с образцом должна быть достаточно очевидной: [b, ...lat] Матчи [1,2,3] где b = 1 а также lat = [2,3], Таким образом, это просто трехслойное уравнение:

• Когда вторым аргументом является пустой список, функция "сборщик" col сразу получает два пустых списка в качестве двух аргументов;

• Когда элемент заголовка второго аргумента (который является списком) совпадает с первым аргументом, результат такой же, как и для рекурсии с хвостом списка, с измененным коллектором, который - после того, как он получит два аргумента, n а также s, - будет предшествовать текущий элемент головы (который a) к s list, и передаст два списка в функцию-коллектор этого вызова col;

• В противном случае элемент head будет добавлен к n список, после n а также s получены построенным коллектором, и оба будут далее поданы в функцию токосъемника.

Другими словами, мы имеем дело с двумя результатами, возвращающимися из рекурсивного вызова, с добавлением головы ко второму, если голова была aили первому, если это не так.

Таким образом, вызов

    (g 1 [ 2, 1, 3, 1, 4, 5 ] col)

то же самое, что (вызовет) вызов

    (col [ 2, ...[3, ...[4, ...[5, ...[]]]]]
         [    1, ...[1,            ...[]]  ])

т.е.

    (col [ 2,     3,     4,     5          ]
         [    1,     1                     ])

---

Другой способ взглянуть на это состоит в том, что следующее является другой, эквивалентной формулировкой:

multirember&Co a lat col = g a lat id id where
    id   = (x => x)            ; identity function  
    (f ∘ g) x = f (g x)        ; function composition
    g a [b, ...lat] c d 
                | b == a  =  g a lat  c     (d ∘ (x => (cons b x)))  ;    (d ∘ {cons b})
                | else    =  g a lat (c ∘ (x => (cons b x)))    d    ; (c ∘ {cons b})
    g a []          c d   =  col     (c [])                  (d [])

и поэтому

multirember&Co 1 [ 2, 1, 3, 1, 4, 5 ] col 
=
col (((((id ∘ {cons 2}) ∘ {cons 3}) ∘ {cons 4}) ∘ {cons 5}) [])   ; { } is for
    ( ( (id ∘       {cons 1}) ∘ {cons 1}                  ) [])   ;  partial application
=
col     (id   (cons 2     (cons 3     (cons 4    (cons 5   [])))))
        (id         (cons 1     (cons 1                    []) ) )  

что само собой разумеется то же самое.

В еще одном псевдокоде (со списком) это показывает, что

multirember&Co a lat col  
   = col [ b for b in lat if (b /= a) ] 
         [ b for b in lat if (b == a) ] 
   = ( ((n,s) => col n s) ∘ {partition {/= a}} ) lat

за исключением того, что только один обход списка lat выполняется (в исходном коде), эффективно, построение вложенной цепочки лямбда-функций, имитирующих исходную структуру списка; какая цепочка затем оценивается для создания двух результатов, передавая их самой верхней функции коллектора col,

Все это показывает нам силу стиля продолжения-прохождения (что и есть) для создания собственного протокола вызова функции, например, для передачи двух результатов от каждого вызова рекурсивной функции, хотя обычно в лямбда-исчислении a Функция может иметь только один результат (даже если, скажем, пара).

Answer 6

Код не строит решение, как это обычно бывает, но он строит код, который вычисляет решение, точно так же, как когда вы строите дерево, используя операции низкого уровня, например cons, +, -и т. д. вместо использования аккумуляторов или фильтров высокого уровня.

Вот почему трудно сказать, является ли процесс итеративным или рекурсивным, потому что, по определению итерационных процессов, они используют конечный объем памяти для локального состояния. Однако этот тип процесса использует много памяти, но он выделяется в среде, а не в локальных параметрах.

Во-первых, здесь я продублирую код, чтобы увидеть переписку без особой прокрутки:

(define multirember&co
  (lambda (a lat col)
    (cond
     ((null? lat)
      (col (quote ()) (quote ())))
     ((eq? (car lat) a)
      (multirember&co a
                      (cdr lat)
                      (lambda (newlat seen)
                        (col newlat
                             (cons (car lat) seen)))))
     (else
      (multirember&co a
                      (cdr lat)
                      (lambda (newlat seen)
                        (col (cons (car lat) newlat)
                             seen)))))))

Давайте попробуем разделить проблему, чтобы увидеть, что на самом деле происходит.

• Случай 1:

---

(multirember&co 'a
                '()
                (lambda (x y) (list x y)))

is the same as    

(let ((col (lambda (x y) (list x y))))
  (col '() '()))

Это тривиальный случай, он никогда не зацикливается.

Теперь интересные случаи:

• Случай 2:

---

(multirember&co 'a
                '(x)
                (lambda (x y) (list x y)))

is the same as    

(let ((col
       (let ((col (lambda (x y) (list x y)))
             (lat '(x))
             (a 'a))
         (lambda (newlat seen)
           (col (cons (car lat) newlat)
                seen)))))
  (col '() '()))

В этом случае процесс выдает этот код как результат и, наконец, оценивает его. Обратите внимание, что локально это все еще хвостовая рекурсия, но в глобальном масштабе это рекурсивный процесс, и он требует памяти не путем выделения некоторой структуры данных, а из-за того, что оценщик выделяет только кадры среды. Каждый цикл углубляет среду, добавляя 1 новый кадр.

• Дело 3

---

(multirember&co 'a
                '(a)
                (lambda (x y) (list x y)))

is the same as    

(let ((col
       (let ((col (lambda (x y) (list x y)))
             (lat '(a))
             (a 'a))
         (lambda (newlat seen)
           (col newlat
                (cons (car lat) seen))))))
  (col '() '()))

Это создает код, но в другой ветви, который накапливает результат в другой переменной.

---

Все остальные случаи представляют собой комбинации 1 из этих 3 случаев, и становится ясно, как действует каждый из 1, добавляя новый слой.

Answer 7

Я надеюсь, что это прохождение поможет

Как предложил Крис, я переименовал newlat/seen в n/s и добавил индекс. Книга дает ужасные названия для функций (друг-новый-новенький-последний-жареный), поэтому я просто сохранил L (для лямбды) и определение.

multirember&co 'tuna '(strawberries tuna and swordfish) a-friend)
  multirember&co 'tuna '(tuna and swordfish) (L(n1 s1)(a-friend (cons 'strawberries n1) s1))
    multirember&co 'tuna '(and swordfish) (L(n2 s2)((L(n1 s1)(a-friend (cons 'strawberries n1) s1)) n2 (cons 'tuna s2))
      multirember&co 'tuna '(swordfish) (L(n3 s3)((L(n2 s2)((L(n1 s1)(a-friend (cons 'strawberries n1) s1)) n2 (cons 'tuna s2)) (cons 'and n3) s3))
        multirember&co 'tuna '() (L(n4 s4)((L(n3 s3)((L(n2 s2)((L(n1 s1)(a-friend (cons 'strawberries n1) s1)) n2 (cons 'tuna s2)) (cons 'and n3) s3)) (cons 'swordfish n4) s4))

((lambda(n4 s4)((lambda(n3 s3)((lambda(n2 s2)((lambda(n1 s1)(a-friend (cons 'strawberries n1) s1)) n2 (cons 'tuna s2))) (cons 'and n3) s3)) (cons 'swordfish n4) s4)) '() '())
               ((lambda(n3 s3)((lambda(n2 s2)((lambda(n1 s1)(a-friend (cons 'strawberries n1) s1)) n2 (cons 'tuna s2))) (cons 'and n3) s3)) '(swordfish) '())
                              ((lambda(n2 s2)((lambda(n1 s1)(a-friend (cons 'strawberries n1) s1)) n2 (cons 'tuna s2))) '(and swordfish) '())
                                             ((lambda(n1 s1)(a-friend (cons 'strawberries n1) s1)) '(and swordfish) '(tuna))
                                                            (a-friend '(strawberries and swordfish) '(tuna))