Как вычислить минимальное связующее дерево узкого места за линейное время?
Мы можем найти минимальное остовное дерево узкого места в O(E log*V) в худшем случае, используя алгоритм Крускала. Это связано с тем, что каждое минимальное остовное дерево является минимальным остовным деревом.
Но я застрял на этом вопросе собеседования из этого курса.
Как мы можем найти минимальное остовное дерево узкого места за линейное время даже в худшем случае. Обратите внимание, что мы можем предположить, что мы можем вычислить медиану n клавиш за линейное время в худшем случае.
4 ответа
- Получить
V, медиана весов |E| кромки. - Найти значение всех ребер не более
Vи получить подграф- Если подграф связан,
Vверхний предел ответа, и уменьшитьVповторите шаг 1, 2. - Если подграф не связан, позвольте подключенному компоненту стать узлом и увеличьте
Vповторите шаг 1, 2.
- Если подграф связан,
Тогда вы сможете решить вопрос за линейное время.
PS: Использование DFS для оценки подграфа связано. и сложность O(E/2) + O(E/4) + O(E/8) + ... = O(E)
Стандартный алгоритм поиска связующего дерева с минимальным узким местом (MBST) известен как алгоритм Камерини. Он работает за линейное время и выглядит следующим образом:
1. Find a median edge weight in graph and partition all edges in to two
partitions A and B around it. Let A have all edges greater than
pivot and B has all edges less than or equal to pivot.
2. Run DFS or BFS on partition B. If it connected graph then again run
step 1 on it.
3. If partition B wasn't a connected graph then we must have more than
1 connected components in it. Create a new graph by contracting each
of these connected components as a single vertex and select edges
from partition A that connects these components. MBST is given by
edges in connected components + MBST of new graph.
В псевдокоде:
1: procedure MBST(V, E)
2: if |E| = 1 then
3: Return E
4: else
5: A, B ← Partition E in two halves around median
6: A is higher half, B is lower half
7: F ← Connected components of B
8: if |F| = 1 and spans all vertices then
9: Return MBST(V, B)
10: else
11: V' ← create one vertex for each connected component in F
12: plus vertices missing from F
13: B' ← Edges from A that connects components in F
14: and edges to vertices not in F
15: Return F ∪ MBST(V', B')
16: end if
17: end if
18: end procedure
Замечания по реализации:
- Медиана может быть найдена в O (n).
- Строка 7 может генерировать структуру данных с несвязанными множествами, используя BFS или DFS.
- Строка 13 включает в себя фильтрацию ребер в A, где у каждого ребра есть конечные точки, которые находятся либо в двух разных соединенных компонентах в F, либо одна конечная точка - это вершина не в F, а другая - в F, или оба не в F. Этот тест может быть выполнен с использованием эффективного структура данных с непересекающимися наборами в O(1) амортизированное время для каждого ребра.
Обновление: я также создал страницу Википедии на эту тему.
Я обнаружил, что другие ответы не содержат подробностей, сбивают с толку или просто неверны Например, ответ ShitalShah гласит:
Создайте новый граф, сжимая каждый из этих соединенных компонентов как одну вершину и выбирая ребра из раздела A, который соединяет эти компоненты
Затем в его псевдокод позже:
11: V' ← create one vertex for each connected component in F
12: plus vertices missing from F
13: B' ← Edges from A that connects components in F
14: and edges to vertices not in F
"Вершины, отсутствующие в F" или "Ребра в вершинах, не принадлежащих F", не упоминаются в описании, непосредственно предшествующем псевдокоду. Если мы позволим этому слайду, мы скоро обнаружим больше расхождений:
Строка 13 включает в себя фильтрацию ребер в A, где у каждого ребра есть конечные точки, которые находятся либо в двух разных соединенных компонентах в F, либо одна конечная точка является вершиной не в F, а другая - в F, или оба не в F.
Какие? Описание и псевдокод говорили о соединении различных подключенных компонентов, используя большие ребра, и теперь мы внезапно отфильтровываем их???
Там еще: ссылка на фактический алгоритм возвращает 403 запрещенных. Статья в Википедии чревата подобными несоответствиями. Как мы можем создать супер вершину, когда они полностью вырождаются в одну вершину на каждый связанный компонент? Как обрабатывать параллельные ребра из раздела А после сжатия - какой из них выбрать? $&T^$#)*)
Я считаю, что, пытаясь дать ответ, мы должны предположить, что читатель знает, где мы живем. Таким образом, я представляю рабочий код, вероятно, единственный найденный в Интернете. Барабанная дробь.
public class MBST<E> {
private static final NumberFormat formatter = NumberFormat.getNumberInstance(Locale.ENGLISH);
static {
formatter.setMinimumFractionDigits(2);
formatter.setMaximumFractionDigits(2);
}
private final UndirectedGraph<E> mbst;
public MBST(UndirectedGraph<E> g) {
System.out.printf("Graph:%n%s", g);
if (g.numEdges() <= 1) {
mbst = g;
return;
}
// can we calculate mean more efficiently?
DoubleSummaryStatistics stats = g.edges().stream()
.collect(summarizingDouble(e -> e.weight));
System.out.printf("Mean: %s%n", formatter.format(stats.getAverage()));
Map<Boolean, List<Edge<E>>> edgeMap = g.edges().stream()
.collect(groupingBy(e -> e.weight < stats.getAverage()));
List<Edge<E>> f = edgeMap.getOrDefault(true, emptyList());
if (f.isEmpty()) {
mbst = g;
return;
}
UndirectedGraph<E> b = new UndirectedGraph<>(f);
ConnectedComponents<E> cc = new ConnectedComponents<>(b);
if (cc.size == 1 && b.numVertices() == g.numVertices()) {
mbst = new MBST<>(b).mbst;
return;
}
Map<Edge<E>, Edge<E>> bPrime = new HashMap<>();
edgeMap.get(false)
.forEach(e1 -> {
boolean vInB = b.containsVertex(e1.v);
boolean wInB = b.containsVertex(e1.w);
boolean edgeInB = vInB && wInB;
E v = vInB ? cc.id(e1.v) : e1.v;
E w = wInB ? cc.id(e1.w) : e1.w;
Edge<E> e2 = new Edge<>(v, w);
bPrime.compute(e2, (key, val) -> {
// same connected component
if (edgeInB && v.equals(w)) return null;
if (val == null || val.weight > e1.weight) return e1;
return val;
});
});
mbst = new MBST<>(new UndirectedGraph<>(bPrime.values())).mbst;
for (Edge<E> e : f) mbst.addEdge(e);
}
public Iterable<Edge<E>> edges() {
return mbst.edges();
}
}
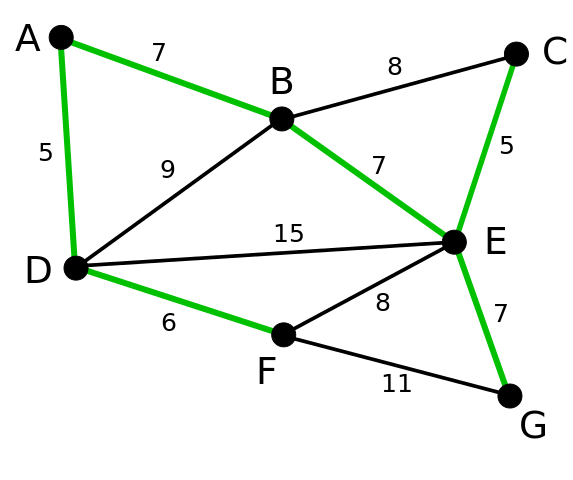
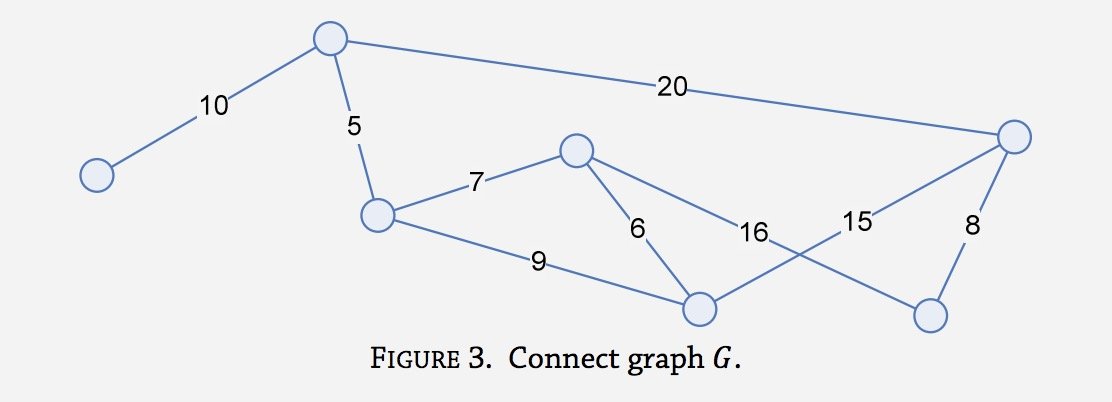
Я проверил это на следующих графиках. Первое изображение из статьи Википедии, второе из этой статьи.
Graph:
Vertices = [A, B, C, D, E, F, G]
Edges = [(A, B), (B, C), (D, E), (E, F), (F, G), (B, D), (C, E), (D, F), (E, G), (A, D), (B, E)]
Mean: 8.00
Graph:
Vertices = [A, B, C, D, E, F, G]
Edges = [(A, B), (C, E), (D, F), (E, G), (A, D), (B, E)]
Mean: 6.17
Graph:
Vertices = [A, B, E, G]
Edges = [(A, B), (E, G), (B, E)]
Mean: 7.00
Graph:
Vertices = [A, B, C, D, E, F, G]
Edges = [(A, B), (B, C), (C, D), (D, E), (F, G), (C, E), (D, F), (E, G), (B, G)]
Mean: 10.67
Graph:
Vertices = [E, G]
Edges = [(E, G)]
Важно отметить, что код решения в другом ответе здесь неверен. Он не только не может получить линейное время с помощью алгоритма медианы медиан, который строго требуется для такой временной сложности, но и использует среднее значение вместо медианы и делит список на потенциально неравные части, что может вызвать бесконечный цикл или O(mn) время, и оба они нарушают предположения исходного алгоритма Камерини. Очень ограниченные тестовые случаи недостаточны для доказательства того, что такой алгоритм работает, требуется большое их количество, прежде чем эмпирическая проверка может считаться адекватной.
Вот код Python, который решит проблему, используя алгоритм Камерини с надлежащей временной сложностью. Алгоритм медианы медиан довольно длинный, но это единственный способ его достичь. Предоставляется пример из Википедии, а также функция визуализации с использованием графвиза. Предполагается, что вы говорите о неориентированных графах на вопрос, ссылающийся на Крускала с O(m log n). Здесь есть некоторая ненужная матрица смежности для преобразования списка ребер, которая составляет O(n^2), но ее можно легко оптимизировать.
def adj_mat_to_edge_list(adj_mat):
#undirected graph needs reflexivity check
return {i+1:[j+1 for j, y in enumerate(row) if not y is None or not adj_mat[j][i] is None]
for i, row in enumerate(adj_mat)}
def adj_mat_to_costs(adj_mat):
return {(i+1, j+1): adj_mat[i][j] for i, row in enumerate(adj_mat)
for j, y in enumerate(row) if not y is None or not adj_mat[j][i] is None}
def partition5(l, left, right):
i = left + 1
while i <= right:
j = i
while j > left and l[j-1] > l[j]:
l[j], l[j-1] = l[j-1], l[j]
j -= 1
i += 1
return (left + right) // 2
def pivot(l, left, right):
if right - left < 5: return partition5(l, left, right)
for i in range(left, right+1, 5):
subRight = i + 4
if subRight > right: subRight = right
median5 = partition5(l, i, subRight)
l[median5], l[left + (i-left) // 5] = l[left + (i-left) // 5], l[median5]
mid = (right - left) // 10 + left + 1
return medianofmedians(l, left, left + (right - left) // 5, mid)
def partition(l, left, right, pivotIndex, n):
pivotValue = l[pivotIndex]
l[pivotIndex], l[right] = l[right], l[pivotIndex]
storeIndex = left
for i in range(left, right):
if l[i] < pivotValue:
l[storeIndex], l[i] = l[i], l[storeIndex]
storeIndex += 1
storeIndexEq = storeIndex
for i in range(storeIndex, right):
if l[i] == pivotValue:
l[storeIndexEq], l[i] = l[i], l[storeIndexEq]
storeIndexEq += 1
l[right], l[storeIndexEq] = l[storeIndexEq], l[right]
if n < storeIndex: return storeIndex
if n <= storeIndexEq: return n
return storeIndexEq
def medianofmedians(l, left, right, n):
while True:
if left == right: return left
pivotIndex = pivot(l, left, right)
pivotIndex = partition(l, left, right, pivotIndex, n)
if n == pivotIndex: return n
elif n < pivotIndex: right = pivotIndex - 1
else: left = pivotIndex + 1
def bfs(g, s):
n, L = len(g), {}
#for i in range(1, n+1): L[i] = 0
L[s] = None; S = [s]
while len(S) != 0:
u = S.pop(0)
for v in g[u]:
if not v in L: L[v] = u; S.append(v)
return L
def mbst(g, costs):
if len(g) == 2 and len(g[next(iter(g))]) == 1: return g
l = [(costs[(x, y)], (x, y)) for x in g for y in g[x] if x < y]
medianofmedians(l, 0, len(l) - 1, len(l) // 2)
A, B = l[len(l)//2:], l[:len(l)//2]
Gb = {}
for _, (x, y) in B:
if x > y: continue
if not x in Gb: Gb[x] = []
if not y in Gb: Gb[y] = []
Gb[x].append(y)
Gb[y].append(x)
F, Fr, S = {}, {}, set(Gb)
while len(S) != 0:
C = set(bfs(Gb, next(iter(S))))
S -= C
root = next(iter(C))
F[root] = C
for x in C: Fr[x] = root
if len(F) == 1 and len(Fr) == len(g): return mbst(Gb, costs)
else:
Ga, ca, mp = {}, {}, {}
for _, (x, y) in A:
if x > y or (x in Fr and y in Fr): continue
if x in Fr:
skip = (Fr[x], y) in ca
if not skip or ca[(Fr[x], y)] > costs[(x, y)]:
ca[(Fr[x], y)] = ca[(y, Fr[x])] = costs[(x, y)]
if skip: continue
mp[(Fr[x], y)] = (x, y); mp[(y, Fr[x])] = (y, x)
x = Fr[x]
elif y in Fr:
skip = (x, Fr[y]) in ca
if not skip or ca[(x, Fr[y])] > costs[(x, y)]:
ca[(x, Fr[y])] = ca[(Fr[y], x)] = costs[(x, y)]
if skip: continue
mp[(x, Fr[y])] = (x, y); mp[(Fr[y], x)] = (y, x)
y = Fr[y]
else: ca[(x, y)] = ca[(y, x)] = costs[(x, y)]
if not x in Ga: Ga[x] = []
if not y in Ga: Ga[y] = []
Ga[x].append(y)
Ga[y].append(x)
res = mbst(Ga, ca)
finres = {}
for x in res:
for y in res[x]:
if x > y: continue
if (x, y) in mp: x, y = mp[(x, y)]
if not x in finres: finres[x] = []
if not y in finres: finres[y] = []
finres[x].append(y)
finres[y].append(x)
for x in Gb:
for y in Gb[x]:
if x > y: continue
if not x in finres: finres[x] = []
if not y in finres: finres[y] = []
finres[x].append(y)
finres[y].append(x)
return finres
def camerini(adjmat):
g = mbst(adj_mat_to_edge_list(riskadjmat), adj_mat_to_costs(riskadjmat))
return {x-1: y-1 if not y is None else y for x, y in bfs(g, next(iter(g))).items()}
def operation_risk(riskadjmat):
mst = camerini(riskadjmat)
return max(riskadjmat[mst[x]][x] for x in mst if not mst[x] is None), mst
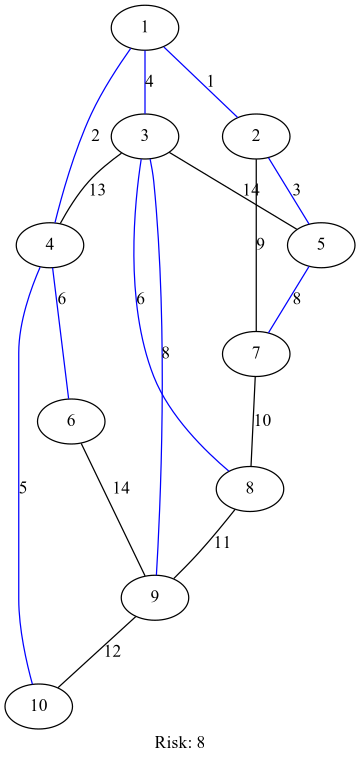
def risk_graph(adjmat, sr):
risk, spantree = sr
return ("graph {" +
"label=\"Risk: " + str(risk) + "\"" +
";".join(str(i+1) + "--" + str(j+1) + "[label=" + str(col) +
(";color=blue" if spantree[i] == j or spantree[j] == i else "") + "]"
for i, row in enumerate(adjmat) for j, col in enumerate(row) if i < j and not col is None) + "}")
riskadjmat = [[None, 1, 4, 2, None, None, None, None, None, None],
[1, None, None, None, 3, None, 9, None, None, None],
[4, None, None, 13, 14, None, None, 6, 8, None],
[2, None, 13, None, None, 6, None, None, None, 5],
[None, 3, 14, None, None, None, 8, None, None, None],
[None, None, None, 6, None, None, None, None, 14, None],
[None, 9, None, None, 8, None, None, 10, None, None],
[None, None, 6, None, None, None, 10, None, 11, None],
[None, None, 8, None, None, 14, None, 11, None, 12],
[None, None, None, 5, None, None, None, None, 12, None]]
import graphviz
graphviz.Source(risk_graph(riskadjmat, operation_risk(riskadjmat)))