Чем минимальное остовное дерево с узким местом отличается от минимального остовного дерева?

Question

Минимальное остовное дерево узкого места взвешенного графа G является остовным деревом G, которое минимизирует максимальный вес любого ребра в остовном дереве. MBST не обязательно является MST (минимальное связующее дерево).

Пожалуйста, приведите пример, где эти заявления имеют смысл.

Answer 1

Посмотрите на пример MST в Википедии для справки:

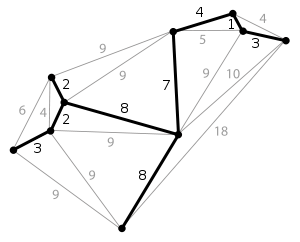
Узкое место в связующем дереве - это край максимального веса в этом дереве. В связующем дереве может быть несколько узких мест (разного веса). В Wikipedia MST есть два узких места весом 8.

Теперь возьмем минимальное остовное дерево данного графа (может быть несколько MST, конечно, с одинаковым общим весом ребер) и назовем максимальный вес ребер B. В нашем примере B = 8.

Любое связующее дерево, которое также имеет узкое место B = 8, является MBST. Но это может быть не MST (потому что общий вес края больше, чем самый лучший).

Итак, возьмите Wikipedia MST и измените его (добавьте / удалите некоторые ребра) так, чтобы

1. это остается связующим деревом, и
2. он все еще не использует вес> 8, пока
3. вы увеличиваете общий вес ребра

Например, измените только поддерево "слева" от MST Википедии (состоящее из весов {2, 2, 3}) на {2, 3, 6}, увеличив общий вес ребра на 4 без изменения узкого места 8. Бинго, вы создали MBST, который не является MST.

Answer 2

Прежде чем ответить на ваш вопрос, позвольте мне определить некоторые термины, которые используются здесь...

1) Spanning Tree: Spanning Tree данного графа - это дерево, которое охватывает все вершины этого графа.

2) Минимальное остовное дерево (MST): MST данного графа является остовным деревом, длина которого минимальна среди всех возможных остовных деревьев этого графа. Более ясно, для данного графа, перечислите все возможные остовные деревья (которые могут быть очень большими) и выберите тот, у которого сумма весов ребер минимальна.

3) Минимальное связующее дерево узкого места (MBST): MBST данного графа является остовным деревом, максимальный вес ребра которого минимален среди всех возможных остовных деревьев. Более четко для данного графа перечислите все возможные остовные деревья и максимальный вес ребер для каждого из остовных деревьев. Среди них выберите остовное дерево, максимальный вес которого минимален.

Теперь давайте посмотрим на следующую картинку с графиком из четырех узлов...

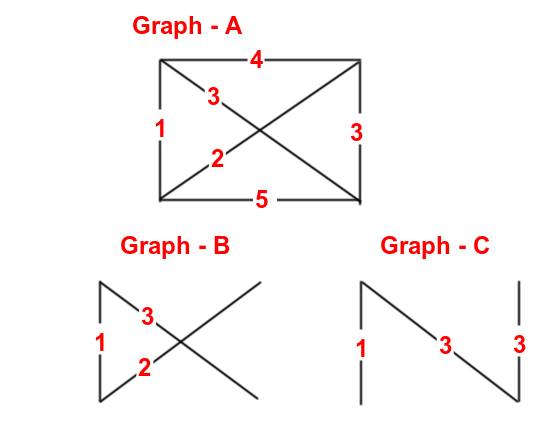
График-A является заданным исходным графом. Если я перечислю все возможные связующие деревья для этого графа и выберу тот, у которого сумма весов ребер минимальна, я получу Graph-B. Таким образом, Graph-B - это минимальное связующее дерево (MST). Обратите внимание, что его общий вес составляет 1+2+3=6.

Теперь, если я выберу остовное дерево с максимальным весом ребер (то есть MBST), то я могу в конечном итоге выбрать Graph-B (или) Graph-C. Обратите внимание, что оба этих остовных дерева имеют максимальный вес ребра 3, который является минимальным среди всех возможных остовных деревьев.

Из Graph-B и Graph-C ясно, что, хотя Graph-C является MBST, это не MST. Потому что его общий вес составляет 1+3+3=7, что больше, чем общий вес MST, нарисованный на графике B (т.е. 6).

Таким образом, MBST не обязательно должен быть MST данного графа. Но MST должен быть MBST.