Найти лучшее / масштаб / сдвиг между двумя векторами

Question

У меня есть два вектора, которые представляют функцию f (x), и другой вектор f (a x + b), т.е. масштабированную и сдвинутую версию f (x). Я хотел бы найти лучшие факторы масштаба и сдвига.

* лучший - с помощью ошибки наименьших квадратов, максимальной вероятности и т. д.

есть идеи?

например:

f1 = [0;0.450541598502498;0.0838213779969326;0.228976968716819;0.91333736150167;0.152378018969223;0.825816977489547;0.538342435260057;0.996134716626885;0.0781755287531837;0.442678269775446;0];
f2 = [-0.029171964726699;-0.0278570165494982;0.0331454732535324;0.187656956432487;0.358856370923984;0.449974662483267;0.391341738643094;0.244800719791534;0.111797007617227;0.0721767235173722;0.0854437239807415;0.143888234591602;0.251750993723227;0.478953530572365;0.748209818420035;0.908044924557262;0.811960826711455;0.512568916956487;0.22669198638799;0.168136111568694;0.365578085161896;0.644996661336714;0.823562159983554;0.792812945867018;0.656803251999341;0.545799498053254;0.587013303815021;0.777464637372241;0.962722388208354;0.980537136457874;0.734416947254272;0.375435649393553;0.106489547770962;0.0892376361668696;0.242467741982851;0.40610516900965;0.427497319032133;0.301874099075184;0.128396341665384;0.00246347624097456;-0.0322120242872125]

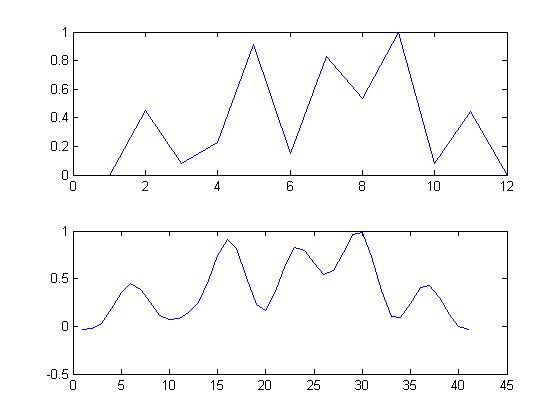
* обратите внимание, что f (x) может быть необратимым...

Спасибо,

Ohad

Answer 1

Вот простой, эффективный, но, возможно, несколько наивный подход.

Сначала убедитесь, что вы делаете общий интерполятор через обе функции. Таким образом, вы можете оценить обе функции между заданными точками данных. Я использовал интерполятор кубических сплайнов, поскольку он кажется достаточно общим для предоставленных вами типов гладких функций (и не требует дополнительных наборов инструментов).

Затем вы оцениваете функцию источника ("оригинал") по большому количеству точек. Используйте это число также в качестве параметра встроенной функции, которая принимает в качестве входных данных X, где

X = [a b] 

(как в ax+b). Для любого входа Xэта встроенная функция вычислит

1. значения функции целевой функции в тех же точках x, но затем масштабируются и смещаются на a а также bсоответственно.

2. Сумма квадратов разностей между результирующими значениями функций и значениями исходной функции, которую вы вычислили ранее.

Используйте эту встроенную функцию в fminsearch с некоторой первоначальной оценкой (той, которую вы получили визуально или автоматически). Для примера, который вы предоставили, я использовал несколько случайных, которые сходились почти к оптимальным.

Все вышеперечисленное в коде:

function s = findScaleOffset

    %% initialize

    f2 = [0;0.450541598502498;0.0838213779969326;0.228976968716819;0.91333736150167;0.152378018969223;0.825816977489547;0.538342435260057;0.996134716626885;0.0781755287531837;0.442678269775446;0];
    f1 = [-0.029171964726699;-0.0278570165494982;0.0331454732535324;0.187656956432487;0.358856370923984;0.449974662483267;0.391341738643094;0.244800719791534;0.111797007617227;0.0721767235173722;0.0854437239807415;0.143888234591602;0.251750993723227;0.478953530572365;0.748209818420035;0.908044924557262;0.811960826711455;0.512568916956487;0.22669198638799;0.168136111568694;0.365578085161896;0.644996661336714;0.823562159983554;0.792812945867018;0.656803251999341;0.545799498053254;0.587013303815021;0.777464637372241;0.962722388208354;0.980537136457874;0.734416947254272;0.375435649393553;0.106489547770962;0.0892376361668696;0.242467741982851;0.40610516900965;0.427497319032133;0.301874099075184;0.128396341665384;0.00246347624097456;-0.0322120242872125];

    figure(1), clf, hold on

    h(1) = subplot(2,1,1); hold on
    plot(f1);
    legend('Original')

    h(2) = subplot(2,1,2); hold on
    plot(f2);

    linkaxes(h)
    axis([0 max(length(f1),length(f2)), min(min(f1),min(f2)),max(max(f1),max(f2))])


    %% make cubic interpolators and test points

    pp1 = spline(1:numel(f1), f1);
    pp2 = spline(1:numel(f2), f2);

    maxX = max(numel(f1), numel(f2));
    N  = 100 * maxX;

    x2 = linspace(1, maxX, N);
    y1 = ppval(pp1, x2);

    %% search for parameters

    s = fminsearch(@(X) sum( (y1 - ppval(pp2,X(1)*x2+X(2))).^2 ), [0 0])

    %% plot results

    y2 = ppval( pp2, s(1)*x2+s(2));

    figure(1), hold on
    subplot(2,1,2), hold on    
    plot(x2,y2, 'r')
    legend('before', 'after')



end

Результаты:

s =
2.886234493867320e-001    3.734482822175923e-001

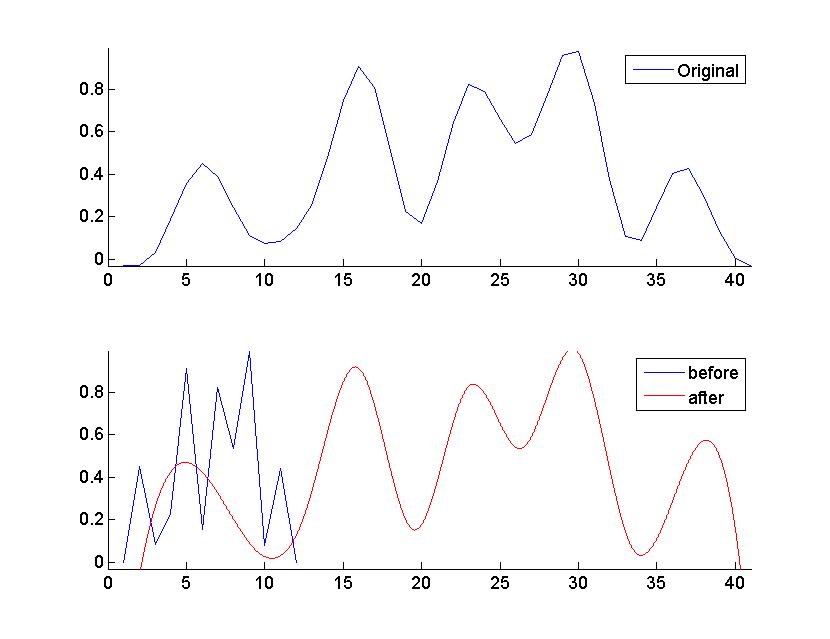
Обратите внимание, что это вычисляет преобразование, противоположное тому, с которым вы сгенерировали данные. В обратном порядке цифры:

>> 1/s(1) 
ans =    
    3.464721948700991e+000   % seems pretty decent 
>> -s(2)
ans = 
    -3.734482822175923e-001  % hmmm...rather different from 7/11!

(Я не уверен относительно предоставленного вами значения 7/11; использование точных значений, которые вы дали для построения графика, приводит к менее точному приближению к функции источника... Вы уверены в 7/11?)

Точность может быть улучшена любым

1. используя другой оптимизатор (fmincon, fminunc, так далее.)
2. требуя более высокой точности от fminsearch через optimset
3. имея больше точек выборки в обоих f1 а также f2 улучшить качество интерполяции
4. Используя лучшую начальную оценку

В любом случае, этот подход довольно общий и дает хорошие результаты. Это также не требует никаких наборов инструментов.

Однако у него есть один существенный недостаток: найденное решение не может быть глобальным оптимизатором, например, качество результатов этого метода может быть весьма чувствительным к первоначальной оценке, которую вы предоставляете. Таким образом, всегда делайте (разницу) график, чтобы убедиться, что окончательное решение является точным, или, если у вас есть большое количество таких вещей, чтобы вычислить какой-то фактор качества, на котором вы решили перезапустить оптимизацию с другим первоначальная оценка.

Конечно, очень возможно использовать результаты преобразований Фурье + Меллина (как предложено Чаохуан ниже) в качестве начальной оценки для этого метода. Это может быть излишним для простого примера, который вы приводите, но я легко могу представить себе ситуации, когда это действительно может быть очень полезно.

Answer 2

Для каждого f(x)принять абсолютное значение f(x) и нормализовать его так, чтобы его можно было считать функцией вероятности над своей поддержкой. Рассчитать ожидаемое значение E[x] и дисперсия Var[x], Тогда у нас есть это

  E[a x + b] = a E[x] + b
Var[a x + b] = a^2 Var[x]

Используйте приведенные выше уравнения и известные значения E[x] а также Var[x] вычислять a а также b, Принимая ваши ценности f1 а также f2 из вашего примера следующий скрипт Octave выполняет эту процедуру:

% Octave script
% f1, f2 are defined as given in your example
f1 = [zeros(length(f2) - length(f1), 1); f1];

save_f1 = f1; save_f2 = f2;

f1 = abs( f1 ); f2 = abs( f2 );
f1 = f1 ./ sum( f1 ); f2 = f2 ./ sum( f2 );

mean = @(x)sum(((1:length(x))' .* x));
var = @(x)sum((((1:length(x))'-mean(x)).^2) .* x);

m1 = mean(f1); m2 = mean(f2);
v1 = var(f1); v2 = var(f2)

a = sqrt( v2 / v1 ); b = m2 - a * m1;

plot( a .* (1:length( save_f1 )) + b, save_f1, ...
      1:length( save_f2 ), save_f2 );
axis([0 length( save_f1 )];

И вывод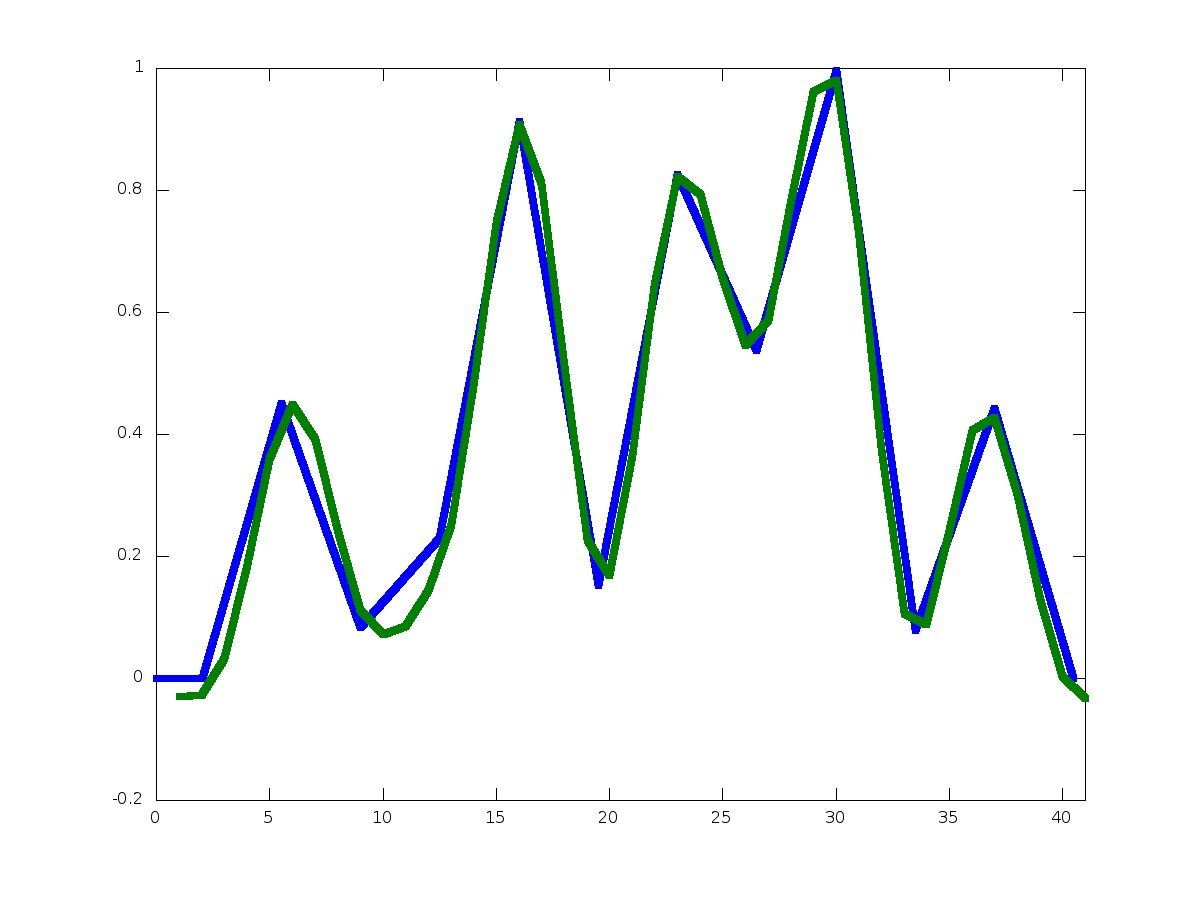

Answer 3

Для масштабного коэффициента а вы можете оценить его, рассчитав отношение амплитудных спектров двух сигналов, поскольку преобразование Фурье инвариантно к сдвигу.

Точно так же вы можете оценить коэффициент сдвига b с помощью преобразования Меллина, которое является масштабно-инвариантным.

Answer 4

Вот супер простой подход к оценке масштаба a это работает на данных вашего примера:

a = length(f2) / length(f1)

Это дает 3.4167, что близко к вашему заявленному значению 3.4. Если эта оценка достаточно хороша, вы можете использовать корреляцию для оценки сдвига.

Я понимаю, что это не совсем то, что вы просили, но это может быть приемлемой альтернативой в зависимости от данных.

Answer 5

Ответы Роди Олденхейса и Джастара верны. Я добавляю свой собственный ответ, просто чтобы подвести итог и соединить их между собой. Я немного испортил код Роди и получил следующее:

function findScaleShift
load f1f2

x0 = [length(f1)/length(f2) 0]; %initial guess, can do better
n=length(f1);
costFunc = @(z) sum((eval_f1(z,f2,n)-f1).^2);
opt.TolFun = eps; 
xopt=fminsearch(costFunc,x0,opt);
f1r=eval_f1(xopt,f2,n);
subplot(211);
plot(1:n,f1,1:n,f1r,'--','linewidth',5)
title(xopt);
subplot(212);
plot(1:n,(f1-f1r).^2);
title('squared error')
end


function y = eval_f1(x,f2,n)
t = maketform('affine',[x(1) 0 x(2); 0 1 0 ; 0 0 1]');
y=imtransform(f2',t,'cubic','xdata',[1 n ],'ydata',[1 1])';
end

Это дает нулевой результат: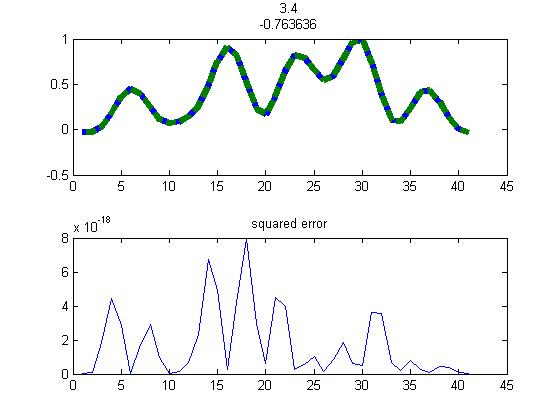Этот метод точный, но исчерпывающий и может занять некоторое время. Другим недостатком является то, что он находит только локальные минимумы и может давать ложные результаты, если первоначальное предположение (x0) далеко.

С другой стороны, метод jstarr дал следующие результаты:

xopt = [ 3.49655562549115         -0.676062367063033]

что составляет 10% отклонения от правильного ответа. Довольно быстрое решение, но не такое точное, как я просил, но все же стоит отметить. Я думаю, что для получения наилучших результатов следует использовать метод jstarr в качестве первоначального предположения о методе, заданном Роди, который дает точное решение.

Ohad