Корректированная по времени формула численного интегрирования Верле
Джонатан Даммер предлагает в Интернете формулу интеграции верлетов, которая называется Verlet с коррекцией по времени. Однако я прочитал несколько сообщений на форуме, что люди получают странные или неожиданные результаты при определенных условиях.
x1 = x + (x – x0) * dt / dt0 + a * dt^2
Существует также ответ на переполнение стека, в котором говорится, что скорректированная по времени формула Даммера нарушена, и постер представляет свой собственный вывод как правильный.
Предложил правильную формулу в ответе stackru
x1 = x + (x – x0) * dt / dt0 + a * dt * (dt + dt0) / 2
Что ж, формула Даммера действительно нарушена? Если да, то лучше ли выводить постер?
PS: также странно, что Dummer использует формулу интеграции verlet x1 = x - x0 + a * dt^2 на своем сайте вместо правильного x1 = 2x - x0 + a * dt^2,
3 ответа
Страница википедии Интеграция Verlet - непостоянные различия во времени представляют две формулы, без ссылки. Я сам не проверял вывод, но аргументы в пользу второй улучшенной формулы выглядят неплохо.
Я скачал электронную таблицу Dummer и изменил одну из формул, чтобы использовать исправление. Результаты намного лучше.
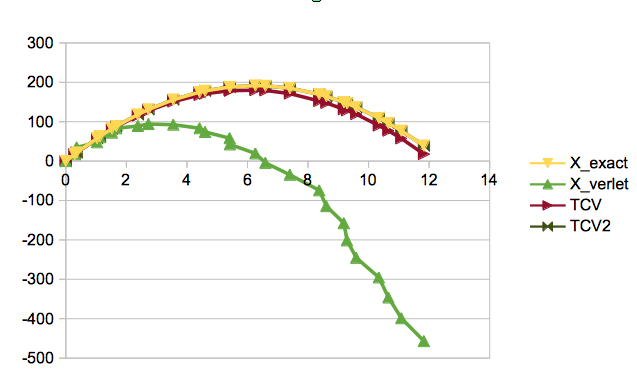
Точные результаты выделены желтым цветом, мы видим, что использование обычного алгоритма Верле с флуктуирующей частотой кадров - это плохо. Правильный по времени вариант Dummer в красном довольно хорош, но немного не в порядке. Темно-зеленая версия с улучшенной коррекцией намного лучше.
Для снарядов под действием силы тяжести, которые имеют квадратичное решение, вы можете обнаружить, что улучшенная версия является точной. Когда степень становится немного выше, она будет отличаться от истинного пути, и, возможно, стоит проверить, получим ли мы еще лучшее приближение.
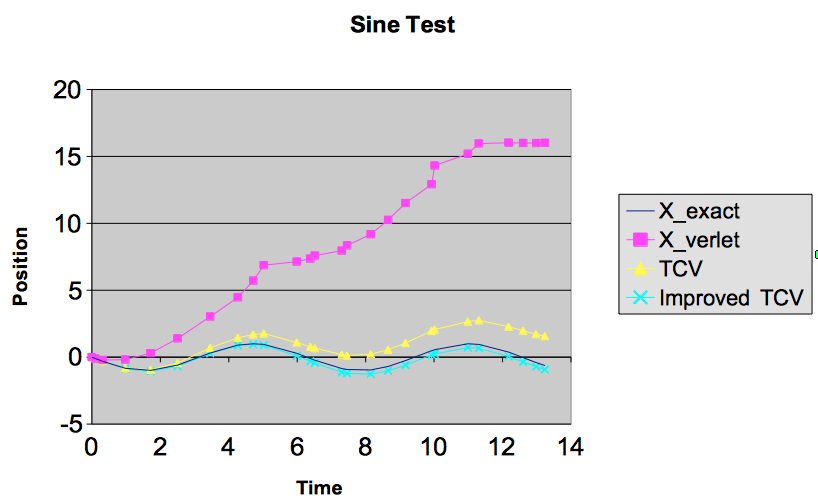
Выполнение того же вычисления для кривой sin показывает, что улучшенный метод значительно лучше. Здесь верный по времени Верлет дрейфует совсем немного. Улучшенная версия лучше, только немного не точный ответ.
Для PS. Обратите внимание, что если вы установите dt=dt0 в формуле TCV
x1 = x + (x – x0) * dt / dt0 + a * dt^2
ты получаешь
x1 = x + x – x0 + a * dt^2
= 2 x – x0 + a * dt^2
оригинальная формула Верле.
Истинный вывод основан на формулах Тейлора
x(t-h0) = x(t) - x'(t)*h0 + 0.5*x''(t)*h0^2 + O(h0^3)
x(t+h1) = x(t) + x'(t)*h1 + 0.5*x''(t)*h1^2 + O(h1^3)
а теперь ликвидируй x'(t) из этих двух формул, чтобы получить формулу, подобную Verlet
h0*x(t+h1) + h1*x(t-h0) = (h0+h1)*x(t) + 0.5*a(t)*h0*h1*(h0+h1) +O(h^3)
которая делает формулу распространения
x(t+h1) = (1+h1/h0)*x(t) - h1/h0*x(t-h0) + 0.5*a(t)*h1*(h0+h1)
= x(t) + (x(t)-x(t-h0))*h1/h0 + 0.5*a(t)*h1*(h0+h1)
так что действительно исправленная формула является правильной.
Обратите внимание, что если вы используете скорость шагов Верле
Verlet(dt) {
v += a * 0.5*dt
x += v*dt
a = acceleration(x)
v += a * 0.5*dt
}
тогда каждый шаг является независимо симплектическим, так что изменение размера шага между шагами абсолютно не вызывает проблем. тогда
Я решил перестать быть ленивым и показать своего рода вывод о том, как оригинальный метод Verlet выглядит с переменным размером шага. Потому что кажется, что эта неправильная адаптация Даммера более распространена, чем я думал, что печально. Я также заметил, что, как указывает приведенный выше ответ, правильная версия теперь находится в Википедии рядом с Dummer, хотя она была добавлена после моего "предложенного правильного ответа".
Когда я смотрю на метод Verlet, я вижу, что он очень похож на скачкообразную, скоростной Verlet, неявный Эйлер и т. Д., Которые выглядят как версии модифицированной средней точки второго порядка, и некоторые из них могут быть идентичными. В каждом из них, в некоторой степени, у них есть идея скачка, где интеграция ускорения (по скорости) и интеграция с постоянной скоростью (по положению) расположены в шахматном порядке так, что они перекрываются наполовину. Это приносит такие вещи, как обратимость времени и стабильность, которые важнее для "реалистичности" симуляции, чем точность. И "реализм", правдоподобность, более важен для видеоигр. Нам все равно, если что-то переместится в положение, немного отличающееся от того, которое действительно вызвало бы его точное количество, при условии, что оно выглядит и ощущается реалистичным. Мы не рассчитываем, куда направить наши мощные спутниковые телескопы, чтобы посмотреть на особенности удаленных объектов или будущих небесных событий. Здесь стабильность и эффективность здесь имеют приоритет над математической точностью. Таким образом, кажется, что метод чехарды является подходящим. Когда вы приспосабливаете чехарду к переменному временному шагу, она теряет часть этого преимущества и теряет часть привлекательности для игровой физики. Stormer-Verlet подобен прыжковой лягушке, за исключением того, что он использует среднюю скорость предыдущего шага вместо отдельно поддерживаемой скорости. Вы можете адаптировать этот Stormer-Verlet так же, как чехарду. Чтобы объединить скорость вперед с фиксированным ускорением, вы используете половину длины предыдущего шага и половину длины следующего шага, потому что они в шахматном порядке. Если бы шаги были зафиксированы как настоящая чехарда, они были бы одинаковой длины, и поэтому две половины длины суммируются в одну. Я использую h для размера шага, a/v/p для ускорения / скорости / положения и hl/pl для "последнего", как в предыдущем шаге. На самом деле это не уравнения, а скорее операции присваивания.
Оригинальная чехарда:
v = v + a*h
p = p + v*h
С переменным шагом по времени:
v = v + a*hl/2 + a*h/2
p = p + v*h
фактор a/2:
v = v + a*(hl + h)/2
p = p + v*h
Использовать предыдущую позицию (p - pl)/hl для начальной скорости:
v = (p - pl)/hl + a*(hl + h)/2
p = p + v*h
Заменить нам не нужно v:
p = p + ( (p - pl)/hl + a*(hl + h)/2)*h
распространять h:
p = p + (p - pl)*h/hl + a*h*(h + hl)/2
Результат не так прост или быстр, как оригинальная форма Штормера Верлета, 2p - pl + a*h^2, Надеюсь, в этом есть какой-то смысл. Вы бы пропустили последний шаг в реальном коде, не нужно умножать h дважды.