Динамическое программирование в Mathematica: как автоматически локализовать и / или очистить определения запомненной функции

Question

В Mathematica 8.0, предположим, у меня есть некоторые константы:

a:=7
b:=9
c:=13
d:=.002
e:=2
f:=1

и я хочу использовать их для оценки некоторых взаимосвязанных функций

g[0,k_]:=0
g[t_,0]:=e
g[t_,k_]:=g[t-1,k]*a+h[t-1,k-1]*b

h[0,k_]:=0
h[t_,0]:=f
h[t_,k_]:=h[t-1,k]*c+g[t-1,k-1]*d

Но это действительно медленно и требует динамического программирования, иначе вы получите экспоненциальное замедление:

g[0, k_] := 0
g[t_, 0] := e
g[t_, k_] := g[t, k] = g[t - 1, k]*a + h[t - 1, k - 1]*b

h[0, k_] := 0
h[t_, 0] := f
h[t_, k_] := h[t, k] = h[t - 1, k]*c + g[t - 1, k - 1]*d

Теперь это действительно быстро, но если мы когда-нибудь захотим изменить константы (скажем, чтобы использовать это в функции манипуляции), мы должны Clearg а также h каждый раз. Если бы у нас были сложные взаимозависимости, было бы очень неприятно очищать их все каждый раз, когда мы хотели получить значение от g а также h,

Есть ли простой способ запустить g а также h в Module или же Block или аналогичный, чтобы я мог получать новый результат каждый раз, когда он оценивается без экспоненциального замедления? Или даже быстрый способ составить таблицу результатов для обоих g а также h в хорошем смысле? Как сказано, я хочу быть в состоянии вычислить g а также h в Manipulate функция.

Answer 1

Вот один из способов, используя Block как вы просили:

ClearAll[defWrap];
SetAttributes[defWrap, HoldFirst];
defWrap[fcall_] :=
  Block[{g, h},
     (* Same defintions with memoization as you had, but within Block*)

     g[0, k_] := 0;
     g[t_, 0] := e;
     g[t_, k_] := g[t, k] = g[t - 1, k]*a + h[t - 1, k - 1]*b;   
     h[0, k_] := 0;
     h[t_, 0] := f;
     h[t_, k_] := h[t, k] = h[t - 1, k]*c + g[t - 1, k - 1]*d;

     (* Our function call, but within a dynamic scope of Block *)
     fcall];

Мы будем использовать это, чтобы дать определения f а также h как

ClearAll[g, h];
g[tt_, kk_] := defWrap[g[tt, kk]];
h[tt_, kk_] := defWrap[h[tt, kk]];

Звоним сейчас:

In[1246]:= g[20,10]//Timing
Out[1246]= {0.,253809.}

In[1247]:= h[20,10]//Timing
Out[1247]= {6.50868*10^-15,126904.}

После каждого вызова не остается глобальных запомненных определений - Block заботится, чтобы уничтожить их непосредственно перед выходом из казни Block, В частности, здесь я изменю параметры и вызову их снова:

In[1271]:= 
a:=1
b:=2
c:=3
d:=.01
e:=4
f:=5

In[1279]:= g[20,10]//Timing
Out[1279]= {0.015,0.808192}

In[1280]:= h[20,10]//Timing
Out[1280]= {0.,1.01024}

Альтернативой этой схеме будет явная передача всех параметров, таких как a,b,c,d,e,f функциям, расширяя их формальные списки параметров (сигнатуры), но это имеет недостаток, заключающийся в том, что более старые запомненные определения, соответствующие различным прошлым значениям параметров, не будут автоматически очищаться. Другая проблема с этим подходом заключается в том, что полученный код будет более хрупким, в зависимости от количества параметров и т. Д.

РЕДАКТИРОВАТЬ

Однако, если вы хотите построить таблицу результатов, это может быть несколько быстрее, поскольку вы делаете это раз и навсегда, и в этом случае вы хотите сохранить все запомненные определения. Итак, вот код:

ClearAll[g, h];
g[0, k_, _] := 0;
g[t_, 0, {a_, b_, c_, d_, e_, f_}] := e;
g[t_, k_, {a_, b_, c_, d_, e_, f_}] := 
     g[t, k, {a, b, c, d, e, f}] = 
        g[t - 1, k, {a, b, c, d, e, f}]*a +  h[t - 1, k - 1, {a, b, c, d, e, f}]*b;

h[0, k_, _] := 0;
h[t_, 0, {a_, b_, c_, d_, e_, f_}] := f;
h[t_, k_, {a_, b_, c_, d_, e_, f_}] := 
     h[t, k, {a, b, c, d, e, f}] = 
        h[t - 1, k, {a, b, c, d, e, f}]*c +  g[t - 1, k - 1, {a, b, c, d, e, f}]*d;

Вы вызываете это, передавая параметры явно:

In[1317]:= g[20,10,{a,b,c,d,e,f}]//Timing
Out[1317]= {0.,253809.}

(Я использовал оригинальные параметры). В этом методе вы можете убедиться, что запомненные определения остаются в глобальной базе правил. В следующий раз, когда вы вызовете функцию с точно такими же параметрами, она извлечет запомненное определение, а не пересчитает. Помимо проблем с этим подходом, которые я описал выше, вы также должны следить за использованием памяти, так как ничего не очищается.

Answer 2

Мемоизация с использованием вспомогательного символа

Техника запоминания, представленная в вопросе, может быть изменена таким образом, чтобы определения g а также h не нужно переустанавливать всякий раз, когда необходимо очистить кеш. Идея состоит в том, чтобы сохранить запомненные значения на вспомогательном символе, а не на g а также h:

g[0,k_] = 0;
g[t_,0] = e;
g[t_,k_] := memo[g, t, k] /. _memo :> (memo[g, t, k] = g[t-1,k]*a+h[t-1,k-1]*b)

h[0,k_] = 0;
h[t_,0] = f;
h[t_,k_] := memo[h, t, k] /. _memo :> (memo[h, t, k] = h[t-1,k]*c+g[t-1,k-1]*d)

Определения, по сути, такие же, как и в оригинальных памятных версиях g а также h кроме того, что новый символ, memo, был введен. С этими определениями кеш можно очистить, просто используя Clear@memo - нет необходимости переопределять g а также h заново. Еще лучше, кеш можно локализовать, поместив memo в Block, таким образом:

Block[{memo, a = 7, b = 9, c = 13, d = 0.002, e = 2, f = 1}
, Table[g[t, k], {t, 0, 100}, {k, 0, 100}]
]

Кэш сбрасывается при выходе из блока.

Мемоизация с помощью совета

Оригинальные и пересмотренные методы запоминания потребовали инвазивных изменений в функции g а также h, Иногда удобно вводить памятку по факту. Один из способов сделать это - использовать метод консультирования - своего рода функциональное программирование, аналог подкласса в ОО-программировании. Конкретная реализация функции совета регулярно появляется на страницах Stackru. Тем не менее, эта техника также агрессивна. Давайте рассмотрим альтернативную технику добавления совета к g а также h без изменения их глобальных определений.

Хитрость будет в том, чтобы временно переопределить g а также h в пределах Block, Переопределения сначала проверяют кэш на результат и, в случае неудачи, вызывают исходные определения вне блока. Давайте вернемся к исходным определениям g а также h которые блаженно не знают о запоминании:

g[0,k_]:=0
g[t_,0]:=e
g[t_,k_]:=g[t-1,k]*a+h[t-1,k-1]*b

h[0,k_]:=0
h[t_,0]:=f
h[t_,k_]:=h[t-1,k]*c+g[t-1,k-1]*d

Основная схема для этой техники выглядит следующим образом:

Module[{gg, hh}
, copyDownValues[g, gg]
; copyDownValues[h, hh]
; Block[{g, h}
  , m:g[a___] := m = gg[a]
  ; m:h[a___] := m = hh[a]
  ; (* ... do something with g and h ... *)
  ]
]

Временные символы gg а также hh вводятся для хранения оригинальных определений g а также h, затем g а также h локально возвращаются к новым определениям кэширования, которые по мере необходимости делегируют исходным определениям. Вот определение copyDownValues:

ClearAll@copyDownValues
copyDownValues[from_Symbol, to_Symbol] :=
  DownValues[to] =
    Replace[
      DownValues[from]
    , (Verbatim[HoldPattern][from[a___]] :> d_) :> (HoldPattern[to[a]] :> d)
    , {1}
    ]

В стремлении сделать этот пост коротким (er), эта функция "копирования" связана только с нижними значениями. Средство общего консультирования также должно учитывать повышающие значения, подзначения, атрибуты символов и так далее.

Этот общий шаблон легко, если утомительно, автоматизировать. Следующая функция макроса memoize делает это, представлен с небольшим комментарием:

ClearAll@memoize
SetAttributes[memoize, HoldRest]
memoize[symbols:{_Symbol..}, body_] :=
  Module[{pairs, copy, define, cdv, sd, s, m, a}
  , pairs = Rule[#, Unique[#, Temporary]]& /@ symbols
  ; copy = pairs /. (f_ -> t_) :> cdv[f, t]
  ; define = pairs /. (f_ -> t_) :> (m: f[a___]) ~sd~ (m ~s~ t[a])
  ; With[{ temps = pairs[[All, 2]]
         , setup1 = Sequence @@ copy
         , setup2 = Sequence @@ define }
    , Hold[Module[temps, setup1; Block[symbols, setup2; body]]] /.
        { cdv -> copyDownValues, s -> Set, sd -> SetDelayed }
    ] // ReleaseHold
  ]

После долгих церемоний мы теперь можем навязывать извне не кеширующие версии g а также h:

memoize[{g, h}
, Block[{a = 7, b = 9, c = 13, d = .002, e = 2, f = 1}
  , Table[g[t, k], {t, 0, 100}, {k, 0, 100}]
  ]
]

Собрав все это вместе, мы можем теперь создать отзывчивый Manipulate блок:

Manipulate[
  memoize[{g, h}
  , Table[g[t, k], {t, 0, tMax}, {k, 0, kMax}] //
      ListPlot3D[#, InterpolationOrder -> 0, PlotRange -> All, Mesh -> None] &
  ]
, {{tMax, 10}, 5, 25}
, {{kMax, 10}, 5, 25}
, {{a, 7}, 0, 20}
, {{b, 9}, 0, 20}
, {{c, 13}, 0, 20}
, {{d, 0.002}, 0, 20}
, {{e, 2}, 0, 20}
, {{f, 1}, 0, 20}
, LocalizeVariables -> False
, TrackedSymbols -> All
]

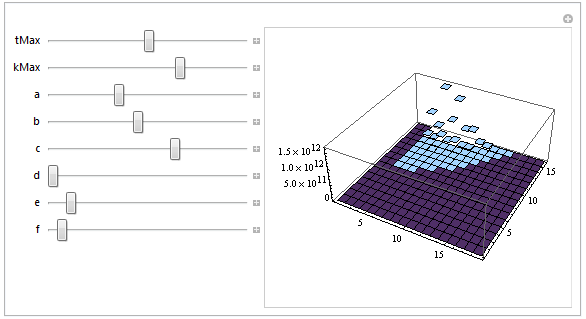
LocalizeVariables а также TrackedSymbols параметры являются артефактами зависимостей, которые g а также h иметь на глобальных символах a через f,