Что находится в вашей сумке для инструментов Mathematica?
Мы все знаем, что Mathematica великолепна, но ей также часто не хватает критически важной функциональности. Какие внешние пакеты / инструменты / ресурсы вы используете с Mathematica?
Я отредактирую (и предложу кому-нибудь еще сделать это) этот основной пост, включив в него ресурсы, посвященные общей применимости в научных исследованиях и которые как можно больше людей найдут полезными. Не стесняйтесь вносить что угодно, даже небольшие фрагменты кода (как я сделал ниже для процедуры синхронизации).
Кроме того, недокументированные и полезные функции в Mathematica 7 и более поздних версиях, которые вы нашли или нашли в какой-то статье / сайте, приветствуются.
Пожалуйста, включите краткое описание или комментарий о том, почему что-то великолепно или какую утилиту он предоставляет. Если вы ссылаетесь на книги на Amazon с помощью партнерских ссылок, укажите это, например, указав свое имя после ссылки.
Пакеты:
LevelSchemeэто пакет, который значительно расширяет возможности Mathematica по созданию хороших участков. Я использую его, если не для чего-то еще, то для намного, намного улучшенного контроля над тиками кадра / осей. Его новейшая версия называется SciDraw, и она будет выпущена где-то в этом году.- Дэвид Парк
Presentation Package(50 долларов США - бесплатно) - Джереми Майкельсона
grassmannOpsПакет предоставляет ресурсы для выполнения алгебры и исчисления с грассмановыми переменными и операторами, которые имеют нетривиальные коммутационные отношения. - Джона Брауна
GrassmannAlgebraпакет и книга для работы с алгебрами Грассмана и Клиффорда. - RISC (Научно-исследовательский институт символических вычислений) имеет множество пакетов для Mathematica (и других языков), доступных для скачивания. В частности, есть Теорема для автоматического доказательства теорем и множество пакетов для символического суммирования, разностных уравнений и т. Д. На странице программного обеспечения группы "Алгоритмическая комбинаторика".
Инструменты:
MASHпревосходный Perl- скрипт Дэниела Ривза, по сути, обеспечивающий поддержку сценариев для Mathematica v7. (В настоящее время встроено в Mathematica 8 с-scriptопция).-
alternate Mathematica shellс GNU readline входом (с использованием python, *nix только) - Пакет ColourMaths позволяет визуально выбирать части выражения и манипулировать ими. http://www.dbaileyconsultancy.co.uk/colour_maths/colour_maths.html
Ресурсы:
Собственный репозиторий Wolfram
MathSourceИмеет много полезных, если узкие ноутбуки для различных приложений. Также проверьте другие разделы, такие какCurrent Documentation,Coursewareдля лекций,- а также
Demosну, демо.
Книги:
- Программирование Mathematica: продвинутое введение Леонида Шифрина (
web,pdf) является обязательным для чтения, если вы хотите сделать что-то большее, чем цикл For в Mathematica. Мы имеем удовольствие отLeonidсам отвечаю на вопросы тут. - Квантовые методы с Mathematica Джеймсом Ф. Феагином ( амазонка)
- Книга Математики Стивена Вольфрама ( Амазонка) (
web) - Схема Шаума ( амазонка)
- Mathematica в действии Стэна Вагона ( Амазонка) - 600 страниц аккуратных примеров и доходит до Mathematica версии 7. Методы визуализации особенно хороши, некоторые из них вы можете увидеть на авторском
Demonstrations Page, - Основы программирования Mathematica Ричард Гейлорд (
pdf) - Хорошее краткое введение в большинство того, что вам нужно знать о программировании Mathematica. - Поваренная книга Mathematica Сала Мангано, опубликованная O'Reilly 2010, 832 страницы. - Написано в хорошо известном стиле поваренной книги О'Рейли: проблема - решение. Для промежуточных продуктов.
- Дифференциальные уравнения с Mathematica, 3-е изд. Elsevier 2004 Amsterdam от Марты Л. Абелл, Джеймса П. Бразелтона - 893 страницы Для начинающих изучите решение задач DE и Mathematica одновременно.
Недокументированные (или едва документированные) функции:
- Как настроить сочетания клавиш Mathematica. Увидеть
this question, - Как проверить шаблоны и функции, используемые собственными функциями Mathematica. Увидеть
this answer - Как добиться согласованного размера для GraphPlots в Mathematica? Увидеть
this question, - Как составлять документы и презентации с помощью Mathematica. Увидеть
this question,
26 ответов
Я упоминал об этом раньше, но инструмент, который я считаю наиболее полезным, это применение Reap а также Sow который имитирует / расширяет поведение GatherBy:
SelectEquivalents[x_List,f_:Identity, g_:Identity, h_:(#2&)]:=
Reap[Sow[g[#],{f[#]}]&/@x, _, h][[2]];
Это позволяет мне группировать списки по любым критериям и преобразовывать их в процессе. Как это работает, так это то, что функция критерия (f) помечает каждый элемент в списке, затем каждый элемент преобразуется с помощью второй предоставленной функции (g), а конкретный выход контролируется третьей функцией (h). Функция h принимает два аргумента: тег и список собранных элементов, которые имеют этот тег. Предметы сохраняют свой первоначальный порядок, поэтому, если вы установите h = #1& тогда вы получите несортированный Unionкак в примерах для Reap, Но это может быть использовано для вторичной переработки.
В качестве примера его полезности я работал с Wannier90, который выводит пространственно зависимый гамильтониан в файл, где каждая строка представляет собой отдельный элемент в матрице, как показано ниже.
rx ry rz i j Re[Hij] Im[Hij]
Чтобы превратить этот список в набор матриц, я собрал все подсписки, содержащие одну и ту же координату, превратил информацию об элементе в правило (то есть {i,j}-> Re[Hij]+I Im[Hij]) и затем превратил собранные правила вSparseArrayвсе с одним вкладышем:
SelectEquivalents[hamlst,
#[[;; 3]] &,
#[[{4, 5}]] -> (Complex @@ #[[6 ;;]]) &,
{#1, SparseArray[#2]} &]
Честно говоря, это мой швейцарский армейский нож, и он делает сложные вещи очень простыми. Большинство других моих инструментов в некоторой степени относятся к конкретному домену, поэтому я, вероятно, не буду публиковать их. Однако большинство, если не все, из нихSelectEquivalents,
Изменить: это не полностью имитироватьGatherBy в том, что он не может сгруппировать несколько уровней выражения так просто, как GatherBy Можно. Тем не мение, Map прекрасно работает для большинства того, что мне нужно.
Пример: @ Ярослав Булатов попросил самостоятельный пример. Вот одно из моих исследований, которое было значительно упрощено. Итак, скажем, у нас есть набор точек на плоскости
In[1] := pts = {{-1, -1, 0}, {-1, 0, 0}, {-1, 1, 0}, {0, -1, 0}, {0, 0, 0},
{0, 1, 0}, {1, -1, 0}, {1, 0, 0}, {1, 1, 0}}
и мы хотели бы уменьшить количество точек с помощью набора операций симметрии. (Для любопытных мы генерируем небольшую группу каждой точки.) Для этого примера давайте используем четырехкратную ось вращения вокруг оси z.
In[2] := rots = RotationTransform[#, {0, 0, 1}] & /@ (Pi/2 Range[0, 3]);
С помощью SelectEquivalents мы можем сгруппировать точки, которые производят одинаковый набор изображений при этих операциях, т.е. они эквивалентны, используя следующие
In[3] := SelectEquivalents[ pts, Union[Through[rots[#] ] ]& ] (*<-- Note Union*)
Out[3]:= {{{-1, -1, 0}, {-1, 1, 0}, {1, -1, 0}, {1, 1, 0}},
{{-1, 0, 0}, {0, -1, 0}, {0, 1, 0}, {1, 0, 0}},
{{0,0,0}}}
который производит 3 подсписка, содержащие эквивалентные пункты. (Заметка, Union здесь абсолютно необходимо, так как оно гарантирует, что каждая точка создает одно и то же изображение. Первоначально я использовал Sort, но если точка лежит на оси симметрии, она инвариантна относительно поворота вокруг этой оси, давая дополнительное изображение себя. Так, Union устраняет эти дополнительные изображения. Также, GatherBy приведет к тому же результату.) В этом случае точки уже находятся в форме, которую я буду использовать, но мне нужна только репрезентативная точка из каждой группировки, и я хотел бы подсчитать количество эквивалентных точек. Поскольку мне не нужно преобразовывать каждую точку, я использую Identity функция во второй позиции. Для третьей функции мы должны быть осторожны. Первым аргументом, переданным ему, будут изображения точек под поворотами, которые для точки {0,0,0} это список из четырех идентичных элементов, и использование его приведет к сбросу количества. Однако второй аргумент - это просто список всех элементов, которые имеют этот тег, поэтому он будет содержать только {0,0,0}, В коде
In[4] := SelectEquivalents[pts,
Union[Through[rots[#]]]&, #&, {#2[[1]], Length[#2]}& ]
Out[4]:= {{{-1, -1, 0}, 4}, {{-1, 0, 0}, 4}, {{0, 0, 0}, 1}}
Обратите внимание, что этот последний шаг может быть легко выполнен
In[5] := {#[[1]], Length[#]}& /@ Out[3]
Но с этим и менее полным примером выше легко увидеть, как очень сложные преобразования возможны с минимумом кода.
Одним из приятных моментов интерфейса ноутбука Mathematica является то, что он может оценивать выражения на любом языке, а не только в Mathematica. В качестве простого примера рассмотрим создание нового типа входной ячейки оболочки, который передает содержащееся выражение в оболочку операционной системы для оценки.
Сначала определите функцию, которая делегирует оценку текстовой команды внешней оболочке:
shellEvaluate[cmd_, _] := Import["!"~~cmd, "Text"]
Второй аргумент необходим и игнорируется по причинам, которые станут очевидными позже. Далее мы хотим создать новый стиль под названием Shell:
- Откройте новый блокнот.
- Выберите пункт меню Формат / Редактировать таблицу стилей...
- В диалоговом окне рядом с Введите имя стиля: тип
Shell, - Выберите скобку ячейки рядом с новым стилем.
- Выберите пункт меню Ячейка / Показать выражение
- Замените выражение ячейки текстом шага 6, приведенным ниже.
- Еще раз выберите пункт меню Ячейка / Показать выражение
- Закройте диалог.
Используйте следующее выражение ячейки как текст шага 6:
Cell[StyleData["Shell"],
CellFrame->{{0, 0}, {0.5, 0.5}},
CellMargins->{{66, 4}, {0, 8}},
Evaluatable->True,
StripStyleOnPaste->True,
CellEvaluationFunction->shellEvaluate,
CellFrameLabels->{{None, "Shell"}, {None, None}},
Hyphenation->False,
AutoQuoteCharacters->{},
PasteAutoQuoteCharacters->{},
LanguageCategory->"Formula",
ScriptLevel->1,
MenuSortingValue->1800,
FontFamily->"Courier"]
Большая часть этого выражения была скопирована непосредственно из встроенного стиля Программы. Ключевыми изменениями являются следующие строки:
Evaluatable->True,
CellEvaluationFunction->shellEvaluate,
CellFrameLabels->{{None, "Shell"}, {None, None}},
Evaluatable включает функциональность SHIFT+ENTER для ячейки. Оценка вызовет CellEvaluationFunction передача содержимого ячейки и типа содержимого в качестве аргументов (shellEvaluate игнорирует последний аргумент). CellFrameLabels Это просто изюминка, позволяющая пользователю определить, что эта ячейка необычна.
Имея все это, мы можем теперь ввести и оценить выражение оболочки:
- В записной книжке, созданной на шаге выше, создайте пустую ячейку и выберите скобку ячейки.
- Выберите пункт меню Формат / Стиль / Оболочка.
- Введите в ячейку действительную команду оболочки операционной системы (например, "ls" в Unix или "dir" в Windows).
- Нажмите SHIFT + ВВОД.
Лучше всего хранить этот определенный стиль в центральной таблице стилей. Кроме того, функции оценки, такие как shellEvaluate лучше всего определить как заглушки, используя DeclarePackage в init.m, Детали обоих этих действий выходят за рамки этого ответа.
С помощью этой функциональности можно создавать записные книжки, содержащие входные выражения в любом интересующем синтаксисе. Функция оценки может быть написана на чистом Mathematica или делегировать какую-либо или все части оценки внешнему агентству. Имейте в виду, что есть другие крючки, которые относятся к оценке клеток, такие как CellEpilog, CellProlog а также CellDynamicExpression,
Обычный шаблон включает запись текста входного выражения во временный файл, компиляцию файла на каком-либо языке, запуск программы и захват вывода для окончательного отображения в выходной ячейке. При реализации полного решения такого рода необходимо учитывать множество деталей (например, правильно регистрировать сообщения об ошибках), но нужно понимать, что такие вещи можно делать не только так, но и практично.
Что касается меня, именно такие особенности делают интерфейс ноутбука центром моей вселенной программирования.
Обновить
Следующая вспомогательная функция полезна для создания таких ячеек:
evaluatableCell[label_String, evaluationFunction_] :=
( CellPrint[
TextCell[
""
, "Program"
, Evaluatable -> True
, CellEvaluationFunction -> (evaluationFunction[#]&)
, CellFrameLabels -> {{None, label}, {None, None}}
, CellGroupingRules -> "InputGrouping"
]
]
; SelectionMove[EvaluationNotebook[], All, EvaluationCell]
; NotebookDelete[]
; SelectionMove[EvaluationNotebook[], Next, CellContents]
)
Используется таким образом:
shellCell[] := evaluatableCell["shell", Import["!"~~#, "Text"] &]
Сейчас если shellCell[] оценивается, входная ячейка будет удалена и заменена новой входной ячейкой, которая оценивает ее содержимое как команду оболочки.
Тодд Гейли (Wolfram Research) просто прислал мне хороший хак, который позволяет "обернуть" встроенные функции произвольным кодом. Я чувствую, что должен поделиться этим полезным инструментом. Вот ответ Тодда на мой question,
Немного интересной (?) Истории: этот стиль взлома для "обертывания" встроенной функции был изобретен в 1994 году Робби Виллегасом и мной, по иронии судьбы, для функции Message, в пакете под названием ErrorHelp, который я написал для журнала Mathematica Journal. тогда С тех пор многие люди использовали его много раз. Это что-то вроде уловки инсайдера, но я думаю, что будет справедливо сказать, что это стало каноническим способом внедрения вашего собственного кода в определение встроенной функции. Это делает работу хорошо. Конечно, вы можете поместить переменную $ inMsg в любой частный контекст, который вы пожелаете.
Unprotect[Message];
Message[args___] := Block[{$inMsg = True, result},
"some code here";
result = Message[args];
"some code here";
result] /; ! TrueQ[$inMsg]
Protect[Message];
Это не полный ресурс, поэтому я добавляю его сюда в разделе ответов, но я нашел его очень полезным при определении проблем со скоростью (что, к сожалению, является большой частью того, о чем программирует Mathematica).
timeAvg[func_] := Module[
{x = 0, y = 0, timeLimit = 0.1, p, q, iterTimes = Power[10, Range[0, 10]]},
Catch[
If[(x = First[Timing[(y++; Do[func, {#}]);]]) > timeLimit,
Throw[{x, y}]
] & /@ iterTimes
] /. {p_, q_} :> p/iterTimes[[q]]
];
Attributes[timeAvg] = {HoldAll};
Использование тогда просто timeAvg@funcYouWantToTest,
РЕДАКТИРОВАТЬ: г-н Wizard предоставил более простую версию, которая устраняет Throw а также Catch и немного проще разобрать:
SetAttributes[timeAvg, HoldFirst]
timeAvg[func_] := Do[If[# > 0.3, Return[#/5^i]] & @@
Timing @ Do[func, {5^i}]
,{i, 0, 15}]
РЕДАКТИРОВАТЬ: Вот версия из acl (взято отсюда):
timeIt::usage = "timeIt[expr] gives the time taken to execute expr, \
repeating as many times as necessary to achieve a total time of 1s";
SetAttributes[timeIt, HoldAll]
timeIt[expr_] := Module[{t = Timing[expr;][[1]], tries = 1},
While[t < 1., tries *= 2; t = Timing[Do[expr, {tries}];][[1]];];
t/tries]
Internal`InheritedBlock
Недавно я узнал о существовании такой полезной функции, как Internal`InheritedBlockИз этого сообщения Даниэля Лихтблау в официальной группе новостей.
Насколько я понимаю, Internal`InheritedBlock позволяет передать копию исходящей функции внутри Block объем:
In[1]:= Internal`InheritedBlock[{Message},
Print[Attributes[Message]];
Unprotect[Message];
Message[x___]:=Print[{{x},Stack[]}];
Sin[1,1]
]
Sin[1,1]
During evaluation of In[1]:= {HoldFirst,Protected}
During evaluation of In[1]:= {{Sin::argx,Sin,2},{Internal`InheritedBlock,CompoundExpression,Sin,Print,List}}
Out[1]= Sin[1,1]
During evaluation of In[1]:= Sin::argx: Sin called with 2 arguments; 1 argument is expected. >>
Out[2]= Sin[1,1]
Я думаю, что эта функция может быть очень полезна для всех, кому необходимо временно изменить встроенные функции!
Сравнение с блоком
Давайте определим некоторую функцию:
a := Print[b]
Теперь мы хотим передать копию этой функции в Block объем. Наивное испытание не дает того, что мы хотим
In[2]:= Block[{a = a}, OwnValues[a]]
During evaluation of In[9]:= b
Out[2]= {HoldPattern[a] :> Null}
Теперь пытаюсь использовать отложенное определение в первом аргументе Block (это тоже недокументированная функция):
In[3]:= Block[{a := a}, OwnValues[a]]
Block[{a := a}, a]
Out[3]= {HoldPattern[a] :> a}
During evaluation of In[3]:= b
Мы видим, что в этом случае a работает, но мы не получили копию оригинала a внутри Block объем.
Теперь давайте попробуем Internal`InheritedBlock:
In[5]:= Internal`InheritedBlock[{a}, OwnValues[a]]
Out[5]= {HoldPattern[a] :> Print[b]}
У нас есть копия оригинального определения для a внутри Block объем, и мы можем изменить его так, как мы хотим, не влияя на глобальное определение a!
Mathematica - острый инструмент, но он может поразить вас своим нетипичным поведением и лавинами загадочных диагностических сообщений. Один из способов справиться с этим - определить функции, следующие этой идиоме:
ClearAll@zot
SetAttributes[zot, ...]
zot[a_] := ...
zot[b_ /; ...] := ...
zot[___] := (Message[zot::invalidArguments]; Abort[])
Это много шаблонов, которые я часто испытываю, чтобы пропустить. Особенно при прототипировании, что часто случается в Mathematica. Итак, я использую макрос define это позволяет мне оставаться дисциплинированным, с гораздо меньшим количеством шаблонов.
Основное использование define это так:
define[
fact[0] = 1
; fact[n_ /; n > 0] := n * fact[n-1]
]
fact[5]
120
На первый взгляд это не так уж и много, но есть некоторые скрытые преимущества. Первый сервис, который define обеспечивает то, что он автоматически применяется ClearAll к определенному символу. Это гарантирует отсутствие оставшихся определений - обычное явление во время первоначальной разработки функции.
Второй сервис заключается в том, что определяемая функция автоматически "закрывается". Под этим я подразумеваю, что функция выдаст сообщение и прервет работу, если она вызывается со списком аргументов, который не соответствует ни одному из определений:
fact[-1]
define::badargs: There is no definition for 'fact' applicable to fact[-1].
$Aborted
Это основная ценность define, который ловит очень распространенный класс ошибок.
Другое удобство - это краткий способ указать атрибуты определяемой функции. Давайте сделаем функцию Listable:
define[
fact[0] = 1
; fact[n_ /; n > 0] := n * fact[n-1]
, Listable
]
fact[{3, 5, 8}]
{6, 120, 40320}
В дополнение ко всем нормальным атрибутам, define принимает дополнительный атрибут с именем Open, Это мешает define от добавления определения всеобщей ошибки в функцию:
define[
successor[x_ /; x > 0] := x + 1
, Open
]
successor /@ {1, "hi"}
{2, successor["hi"]}
Несколько функций могут быть определены для функции:
define[
flatHold[x___] := Hold[x]
, {Flat, HoldAll}
]
flatHold[flatHold[1+1, flatHold[2+3]], 4+5]
Hold[1 + 1, 2 + 3, 4 + 5]
Без дальнейших церемоний, вот определение define:
ClearAll@define
SetAttributes[define, HoldAll]
define[body_, attribute_Symbol] := define[body, {attribute}]
define[body:(_Set|_SetDelayed), attributes_List:{}] := define[CompoundExpression[body], attributes]
define[body:CompoundExpression[((Set|SetDelayed)[name_Symbol[___], _])..], attributes_List:{}] :=
( ClearAll@name
; SetAttributes[name, DeleteCases[attributes, Open]]
; If[!MemberQ[attributes, Open]
, def:name[___] := (Message[define::badargs, name, Defer@def]; Abort[])
]
; body
;
)
def:define[___] := (Message[define::malformed, Defer@def]; Abort[])
define::badargs = "There is no definition for '``' applicable to ``.";
define::malformed = "Malformed definition: ``";
Представленная реализация не поддерживает ни up-значения, ни карри, ни шаблоны более общие, чем простое определение функции. Это остается полезным, однако.
Начать без открытой записной книжки
Меня беспокоило то, что Mathematica начала с пустой записной книжки. Я мог бы закрыть эту записную книжку сценарием, но она все равно быстро открылась. Мой хак это создать файл Invisible.nb содержащий:
Notebook[{},Visible->False]
И добавить это в мой Kernel\init.m:
If[Length[Notebooks["Invisible*"]] > 0,
NotebookClose[Notebooks["Invisible*"][[1]]]
]
SetOptions[$FrontEnd,
Options[$FrontEnd, NotebooksMenu] /.
HoldPattern["Invisible.nb" -> {__}] :> Sequence[]
]
Теперь я запускаю Mathematica, открыв Invisible.nb
Может быть, есть и лучший способ, но это мне хорошо послужило.
Индивидуальные Fold а также FoldList
Fold[f, x] сделан эквивалентно Fold[f, First@x, Rest@x]
Между прочим, я полагаю, что это может найти свой путь в будущей версии Mathematica.
Сюрприз! Это было реализовано, хотя в настоящее время это не документировано. Мне сообщили, что он был реализован в 2011 году Оливером Рюбенкоенигом, по-видимому, вскоре после того, как я опубликовал это. Спасибо Оливер Рюбенкоениг!
Unprotect[Fold, FoldList]
Fold[f_, h_[a_, b__]] := Fold[f, Unevaluated @ a, h @ b]
FoldList[f_, h_[a_, b__]] := FoldList[f, Unevaluated @ a, h @ b]
(* Faysal's recommendation to modify SyntaxInformation *)
SyntaxInformation[Fold] = {"ArgumentsPattern" -> {_, _, _.}};
SyntaxInformation[FoldList] = {"ArgumentsPattern" -> {_, _., {__}}};
Protect[Fold, FoldList]
Обновлено, чтобы разрешить это:
SetAttributes[f, HoldAll]
Fold[f, Hold[1 + 1, 2/2, 3^3]]
f[f[1 + 1, 2/2], 3^3]
"Динамический раздел"
Смотрите новую версию этой функции в посте Mathematica.SE #7512.
Часто я хочу разделить список в соответствии с последовательностью длин.
Пример псевдокода:
partition[{1,2,3,4,5,6}, {2,3,1}]
Выход: {{1,2}, {3,4,5}, {6}}
Я придумал это:
dynP[l_, p_] :=
MapThread[l[[# ;; #2]] &, {{0} ~Join~ Most@# + 1, #} &@Accumulate@p]
Который я тогда закончил с этим, включая проверку аргументов:
dynamicPartition[l_List, p : {_Integer?NonNegative ..}] :=
dynP[l, p] /; Length@l >= Tr@p
dynamicPartition[l_List, p : {_Integer?NonNegative ..}, All] :=
dynP[l, p] ~Append~ Drop[l, Tr@p] /; Length@l >= Tr@p
dynamicPartition[l_List, p : {_Integer?NonNegative ..}, n__ | {n__}] :=
dynP[l, p] ~Join~ Partition[l ~Drop~ Tr@p, n] /; Length@l >= Tr@p
Третий аргумент управляет тем, что происходит с элементами, выходящими за рамки спецификации разделения
Уловки Сабольца по математике
Я чаще всего использую Палитру табличных данных.
CreatePalette@
Column@{Button["TSV",
Module[{data, strip},
data = NotebookGet[ClipboardNotebook[]][[1, 1, 1]];
strip[s_String] :=
StringReplace[s, RegularExpression["^\\s*(.*?)\\s*$"] -> "$1"];
strip[e_] := e;
If[Head[data] === String,
NotebookWrite[InputNotebook[],
ToBoxes@Map[strip, ImportString[data, "TSV"], {2}]]]]],
Button["CSV",
Module[{data, strip},
data = NotebookGet[ClipboardNotebook[]][[1, 1, 1]];
strip[s_String] :=
StringReplace[s, RegularExpression["^\\s*(.*?)\\s*$"] -> "$1"];
strip[e_] := e;
If[Head[data] === String,
NotebookWrite[InputNotebook[],
ToBoxes@Map[strip, ImportString[data, "CSV"], {2}]]]]],
Button["Table",
Module[{data}, data = NotebookGet[ClipboardNotebook[]][[1, 1, 1]];
If[Head[data] === String,
NotebookWrite[InputNotebook[],
ToBoxes@ImportString[data, "Table"]]]]]}
Изменить внешние данные изнутри Compile
Недавно Даниэль Лихтблау показал этот метод, которого я никогда раньше не видел. На мой взгляд, это значительно расширяет полезность Compile
ll = {2., 3., 4.};
c = Compile[{{x}, {y}}, ll[[1]] = x; y];
c[4.5, 5.6]
ll
(* Out[1] = 5.6 *)
(* Out[2] = {4.5, 3., 4.} *)
Общие проблемы экспорта PDF/EMF и их решения
1) Это совершенно неожиданно и недокументировано, но Mathematica экспортирует и сохраняет графику в форматах PDF и EPS, используя набор определений стилей, который отличается от набора, используемого для отображения Блокнотов на экране. По умолчанию блокноты отображаются на экране в среде стиля "Работа" (это значение по умолчанию для ScreenStyleEvironment Глобальный $FrontEnd вариант), но напечатаны в "Printout" среда стиля (которая является значением по умолчанию для PrintingStyleEnvironment Глобальный $FrontEnd опция). Когда кто-то экспортирует графику в растровые форматы, такие как GIF и PNG или в формате EMF, Mathematica генерирует графику, которая выглядит точно так же, как она выглядит внутри Notebook. Кажется, что "Working" В этом случае для рендеринга используется стиль среды. Но это не тот случай, когда вы экспортируете / сохраняете что-либо в форматах PDF или EPS! В этом случае "Printout" среда стиля используется по умолчанию, которая очень сильно отличается от среды стиля "Работа". Прежде всего, "Printout" наборы стилей среды Magnification до 80%. Во-вторых, он использует свои собственные значения для размеров шрифта разных стилей, что приводит к несогласованным изменениям размера шрифта в измененном файле PDF по сравнению с исходным отображением на экране. Последнее можно назвать флуктуациями FontSize, которые очень раздражают. Но, к счастью, этого можно избежать , установив PrintingStyleEnvironment Глобальный $FrontEnd Вариант "Рабочий":
SetOptions[$FrontEnd, PrintingStyleEnvironment -> "Working"]
2) Общая проблема при экспорте в формат EMF состоит в том, что большинство программ (не только Mathematica) генерируют файл, который выглядит хорошо при размере по умолчанию, но становится уродливым при увеличении. Это происходит потому, что метафайлы выбираются с точностью разрешения экрана. Качество созданного файла EMF может быть улучшено Magnify исходный графический объект, так что точность выборки исходной графики становится намного более точной. Сравните два файла:
graphics1 =
First@ImportString[
ExportString[Style["a", FontFamily -> "Times"], "PDF"], "PDF"];
graphics2 = Magnify[graphics1, 10];
Export["C:\\test1.emf", graphics1]
Export["C:\\test2.emf", graphics2]
Если вы вставите эти файлы в Microsoft Word и увеличите их, вы увидите, что у первого "а" есть пилообразный сигнал, а у второго нет (протестировано с Mathematica 6).
Еще один путь через ImageResolution был предложен Крисом Дегненом (этот вариант действует, по крайней мере, начиная с Mathematica 8):
Export["C:\\test1.emf", graphics1]
Export["C:\\test2.emf", graphics1, ImageResolution -> 300]
3) В Mathematica у нас есть три способа конвертировать графику в метафайл: через Export в "EMF" (настоятельно рекомендуется: создает метафайл с максимально возможным качеством), через Save selection As... пункт меню ( производит гораздо менее точную фигуру, не рекомендуется) и через Edit ► Copy As ► Metafile пункт меню ( я настоятельно рекомендую против этого маршрута).
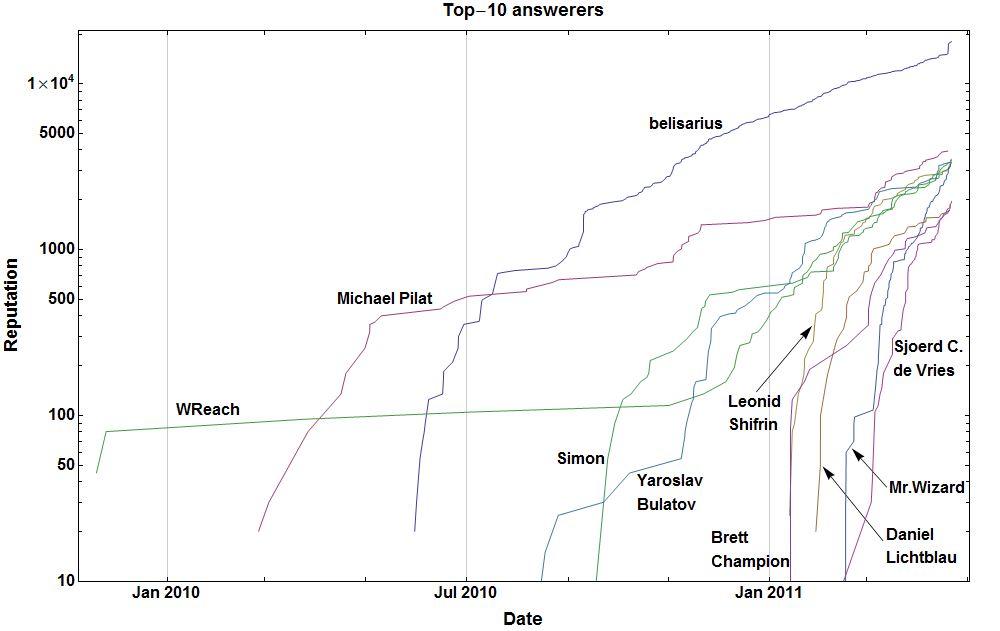
По многочисленным просьбам, код для генерации топ-10 SO отвечает ответчикам (кроме аннотаций) с использованием SO API.
getRepChanges[userID_Integer] :=
Module[{totalChanges},
totalChanges =
"total" /.
Import["http://api.stackru.com/1.1/users/" <>
ToString[userID] <> "/reputation?fromdate=0&pagesize=10&page=1",
"JSON"];
Join @@ Table[
"rep_changes" /.
Import["http://api.stackru.com/1.1/users/" <>
ToString[userID] <>
"/reputation?fromdate=0&pagesize=10&page=" <> ToString[page],
"JSON"],
{page, 1, Ceiling[totalChanges/10]}
]
]
topAnswerers = ({"display_name",
"user_id"} /. #) & /@ ("user" /. ("top_users" /.
Import["http://api.stackru.com/1.1/tags/mathematica/top-\
answerers/all-time", "JSON"]))
repChangesTopUsers =
Monitor[Table[
repChange =
ReleaseHold[(Hold[{DateList[
"on_date" + AbsoluteTime["January 1, 1970"]],
"positive_rep" - "negative_rep"}] /. #) & /@
getRepChanges[userID]] // Sort;
accRepChange = {repChange[[All, 1]],
Accumulate[repChange[[All, 2]]]}\[Transpose],
{userID, topAnswerers[[All, 2]]}
], userID];
pl = DateListLogPlot[
Tooltip @@@
Take[({repChangesTopUsers, topAnswerers[[All, 1]]}\[Transpose]),
10], Joined -> True, Mesh -> None, ImageSize -> 1000,
PlotRange -> {All, {10, All}},
BaseStyle -> {FontFamily -> "Arial-Bold", FontSize -> 16},
DateTicksFormat -> {"MonthNameShort", " ", "Year"},
GridLines -> {True, None},
FrameLabel -> (Style[#, FontSize -> 18] & /@ {"Date", "Reputation",
"Top-10 answerers", ""})]
Кэширование выражений
Я считаю, что эти функции очень полезны для кэширования любого выражения. Интересная вещь для этих двух функций заключается в том, что само удерживаемое выражение используется в качестве ключа хеш-таблицы / символа Cache или CacheIndex, по сравнению с хорошо известным памятником в mathematica, где вы можете кэшировать результат, только если функция определена как f[x_]:= f[x] = ... Таким образом, вы можете кэшировать любую часть кода, это полезно, если функция должна вызываться несколько раз, но только некоторые части кода не должны пересчитываться.
Кэшировать выражение независимо от его аргументов.
SetAttributes[Cache, HoldFirst];
c:Cache[expr_] := c = expr;
Ex: Cache[Pause[5]; 6]
Cache[Pause[5]; 6]
Во второй раз выражение возвращает 6 без ожидания.
Для кэширования выражения используется псевдоним, который может зависеть от аргумента кэшированного выражения.
SetAttributes[CacheIndex, HoldRest];
c:CacheIndex[index_,expr_] := c = expr;
Ex: CacheIndex[{"f",2},x=2;y=4;x+y]
Если для вычисления expr требуется некоторое время, гораздо быстрее вычислить {"f",2}, например, для получения кэшированного результата.
Разновидность этих функций для того, чтобы иметь локализованный кеш (т. Е. Кеш-память автоматически высвобождается за пределами конструкции Block), см. В этом посте. Избегайте повторных обращений к интерполяции.
Удаление кэшированных значений
Удалить кэшированные значения, когда вы не знаете количество определений функции. Я считаю, что определения имеют пробел где-то в своих аргументах.
DeleteCachedValues[f_] :=
DownValues[f] = Select[DownValues[f], !FreeQ[Hold@#,Pattern]&];
Чтобы удалить кэшированные значения, когда вы знаете количество определений функции (идет немного быстрее).
DeleteCachedValues[f_,nrules_] :=
DownValues[f] = Extract[DownValues[f], List /@ Range[-nrules, -1]];
При этом используется тот факт, что определения функции находятся в конце их списка DownValues, а кэшированные значения - раньше.
Использование символов для хранения данных и объектоподобных функций
Также здесь есть интересные функции для использования символов, таких как объекты.
Уже хорошо известно, что вы можете хранить данные в символах и быстро получать к ним доступ, используя DownValues
mysymbol["property"]=2;
Вы можете получить доступ к списку ключей (или свойств) символа, используя эти функции, основываясь на том, что dreeves представил в посте на этом сайте:
SetAttributes[RemoveHead, {HoldAll}];
RemoveHead[h_[args___]] := {args};
NKeys[symbol_] := RemoveHead @@@ DownValues[symbol(*,Sort->False*)][[All,1]];
Keys[symbol_] := NKeys[symbol] /. {x_} :> x;
Я часто использую эту функцию для отображения всей информации, содержащейся в DownValues символа:
PrintSymbol[symbol_] :=
Module[{symbolKeys},
symbolKeys = Keys[symbol];
TableForm@Transpose[{symbolKeys, symbol /@ symbolKeys}]
];
Наконец, вот простой способ создать символ, который ведет себя как объект в объектно-ориентированном программировании (он просто воспроизводит самое основное поведение ООП, но я нахожу синтаксис элегантным):
Options[NewObject]={y->2};
NewObject[OptionsPattern[]]:=
Module[{newObject},
newObject["y"]=OptionValue[y];
function[newObject,x_] ^:= newObject["y"]+x;
newObject /: newObject.function2[x_] := 2 newObject["y"]+x;
newObject
];
Свойства сохраняются как DownValues, а методы - как отложенные Upvalues в символе, созданном модулем, который возвращается. Я нашел синтаксис для function2, который является обычным OO-синтаксисом для функций в структуре данных Tree в Mathematica.
Список существующих типов значений, которые имеет каждый символ, см. По адресу http://reference.wolfram.com/mathematica/tutorial/PatternsAndTransformationRules.html и http://www.verbeia.com/mathematica/tips/HTMLLinks/Tricks_Misc_4.html,
Например попробуйте это
x = NewObject[y -> 3];
function[x, 4]
x.function2[5]
Вы можете пойти дальше, если хотите эмулировать наследование объектов, используя пакет InheritRules, доступный здесь http://library.wolfram.com/infocenter/MathSource/671/
Вы также можете хранить определение функции не в newObject, а в символе типа, поэтому, если NewObject возвращает тип [newObject] вместо newObject, вы можете определить function и function2 как это вне NewObject (и не внутри) и использовать то же, что и раньше,
function[type[object_], x_] ^:= object["y"] + x;
type /: type[object_].function2[x_] := 2 object["y"]+x;
Используйте UpValues [тип], чтобы увидеть, что функция и function2 определены в символе типа.
Дополнительные идеи об этом последнем синтаксисе представлены здесь https://mathematica.stackexchange.com/a/999/66.
Улучшенная версия SelectEquivalents
@rcollyer: Большое спасибо за то, что вывели SelectEquivalents на поверхность, это потрясающая функция. Вот улучшенная версия SelectEquivalents, перечисленных выше, с большим количеством возможностей и опций, это облегчает использование.
Options[SelectEquivalents] =
{
TagElement->Identity,
TransformElement->Identity,
TransformResults->(#2&) (*#1=tag,#2 list of elements corresponding to tag*),
MapLevel->1,
TagPattern->_,
FinalFunction->Identity
};
SelectEquivalents[x_List,OptionsPattern[]] :=
With[
{
tagElement=OptionValue@TagElement,
transformElement=OptionValue@TransformElement,
transformResults=OptionValue@TransformResults,
mapLevel=OptionValue@MapLevel,
tagPattern=OptionValue@TagPattern,
finalFunction=OptionValue@FinalFunction
}
,
finalFunction[
Reap[
Map[
Sow[
transformElement@#
,
{tagElement@#}
]&
,
x
,
{mapLevel}
]
,
tagPattern
,
transformResults
][[2]]
]
];
Вот примеры того, как эта версия может быть использована:
Использование Mathematica Gather/Collect правильно
Как бы вы сделали функцию сводной таблицы в Mathematica?
Mathematica быстрый алгоритм 2D-биннинга
Internal`Bag
Даниэль Лихтблау описывает здесь интересную внутреннюю структуру данных для растущих списков.
Внедрение Quadtree в Mathematica
Функции отладки
Эти два сообщения указывают на полезные функции для отладки:
Как отлаживать при написании маленьких или больших кодов с помощью Mathematica? верстак? мма отладчик? или что-то другое? (Покажи это)
https://stackru.com/questions/5459735/the-clearest-way-to-represent-mathematicas-evaluation-sequence/5527117 (TraceView)
Вот еще одна функция, основанная на Reap и Sow, для извлечения выражений из различных частей программы и сохранения их в символе.
SetAttributes[ReapTags,HoldFirst];
ReapTags[expr_]:=
Module[{elements},
Reap[expr,_,(elements[#1]=#2/.{x_}:>x)&];
elements
];
Вот пример
ftest[]:=((*some code*)Sow[1,"x"];(*some code*)Sow[2,"x"];(*some code*)Sow[3,"y"]);
s=ReapTags[ftest[]];
Keys[s]
s["x"]
PrintSymbol[s] (*Keys and PrintSymbol are defined above*)
Другие источники
Вот список интересных ссылок для целей обучения:
Коллекция учебных ресурсов Mathematica
Обновлено здесь: https://mathematica.stackexchange.com/a/259/66
Мои служебные функции (у меня есть эти встроенные в MASH, который упоминается в вопросе):
pr = WriteString["stdout", ##]&; (* More *)
prn = pr[##, "\n"]&; (* convenient *)
perr = WriteString["stderr", ##]&; (* print *)
perrn = perr[##, "\n"]&; (* statements. *)
re = RegularExpression; (* I wish mathematica *)
eval = ToExpression[cat[##]]&; (* weren't so damn *)
EOF = EndOfFile; (* verbose! *)
read[] := InputString[""]; (* Grab a line from stdin. *)
doList[f_, test_] := (* Accumulate list of what f[] *)
Most@NestWhileList[f[]&, f[], test]; (* returns while test is true. *)
readList[] := doList[read, #=!=EOF&]; (* Slurp list'o'lines from stdin. *)
cat = StringJoin@@(ToString/@{##})&; (* Like sprintf/strout in C/C++. *)
system = Run@cat@##&; (* System call. *)
backtick = Import[cat["!", ##], "Text"]&; (* System call; returns stdout. *)
slurp = Import[#, "Text"]&; (* Fetch contents of file as str. *)
(* ABOVE: mma-scripting related. *)
keys[f_, i_:1] := (* BELOW: general utilities. *)
DownValues[f, Sort->False][[All,1,1,i]]; (* Keys of a hash/dictionary. *)
SetAttributes[each, HoldAll]; (* each[pattern, list, body] *)
each[pat_, lst_, bod_] := ReleaseHold[ (* converts pattern to body for *)
Hold[Cases[Evaluate@lst, pat:>bod];]]; (* each element of list. *)
some[f_, l_List] := True === (* Whether f applied to some *)
Scan[If[f[#], Return[True]]&, l]; (* element of list is True. *)
every[f_, l_List] := Null === (* Similarly, And @@ f/@l *)
Scan[If[!f[#], Return[False]]&, l]; (* (but with lazy evaluation). *)
Одна хитрость, которую я использовал, которая позволяет вам эмулировать способ работы большинства встроенных функций с неверными аргументами (отправка сообщения, а затем возвращение всей формы без оценки), использует причуду пути Condition работает, когда используется в определении. Если foo должен работать только с одним аргументом:
foo[x_] := x + 1;
expr : foo[___] /; (Message[foo::argx, foo, Length@Unevaluated[expr], 1];
False) := Null; (* never reached *)
Если у вас есть более сложные потребности, легко выделить проверку аргументов и генерацию сообщений как независимую функцию. Вы можете делать более сложные вещи, используя побочные эффекты в Condition это не просто генерация сообщений, но, на мой взгляд, большинство из них попадают в категорию "подлых хаков" и их следует избегать, если это возможно.
Также в категории "метапрограммирование", если у вас есть пакет Mathematica (.m), вы можете использовать "HeldExpressions" элемент, чтобы получить все выражения в файле, завернутом в HoldComplete, Это значительно упрощает отслеживание, чем использование текстового поиска. К сожалению, нет простого способа сделать то же самое с ноутбуком, но вы можете получить все входные выражения, используя что-то вроде следующего:
inputExpressionsFromNotebookFile[nb_String] :=
Cases[Get[nb],
Cell[BoxData[boxes_], "Input", ___] :>
MakeExpression[StripBoxes[boxes], StandardForm],
Infinity]
Наконец, вы можете использовать тот факт, что Module эмулирует лексические замыкания для создания эквивалента ссылочных типов. Вот простой стек (который использует Condition трюк для обработки ошибок в качестве бонуса):
ClearAll[MakeStack, StackInstance, EmptyQ, Pop, Push, Peek]
With[{emptyStack = Unique["empty"]},
Attributes[StackInstance] = HoldFirst;
MakeStack[] :=
Module[{backing = emptyStack},
StackInstance[backing]];
StackInstance::empty = "stack is empty";
EmptyQ[StackInstance[backing_]] := (backing === emptyStack);
HoldPattern[
Pop[instance : StackInstance[backing_]]] /;
! EmptyQ[instance] || (Message[StackInstance::empty]; False) :=
(backing = Last@backing; instance);
HoldPattern[Push[instance : StackInstance[backing_], new_]] :=
(backing = {new, backing}; instance);
HoldPattern[Peek[instance : StackInstance[backing_]]] /;
! EmptyQ[instance] || (Message[StackInstance::empty]; False) :=
First@backing]
Теперь вы можете напечатать элементы списка в обратном порядке в излишне запутанном виде!
With[{stack = MakeStack[], list},
Do[Push[stack, elt], {elt, list}];
While[!EmptyQ[stack],
Print[Peek@stack];
Pop@stack]]
Распечатка определений символов системы без добавления контекста
contextFreeDefinition[] Функция ниже попытается напечатать определение символа без добавления наиболее распространенного контекста. Затем определение можно скопировать в Workbench и отформатировать для удобства чтения (выберите его, щелкните правой кнопкой мыши, Source -> Format)
Clear[commonestContexts, contextFreeDefinition]
commonestContexts[sym_Symbol, n_: 1] := Quiet[
Commonest[
Cases[Level[DownValues[sym], {-1}, HoldComplete],
s_Symbol /; FreeQ[$ContextPath, Context[s]] :> Context[s]], n],
Commonest::dstlms]
contextFreeDefinition::contexts = "Not showing the following contexts: `1`";
contextFreeDefinition[sym_Symbol, contexts_List] :=
(If[contexts =!= {}, Message[contextFreeDefinition::contexts, contexts]];
Internal`InheritedBlock[{sym}, ClearAttributes[sym, ReadProtected];
Block[{$ContextPath = Join[$ContextPath, contexts]},
Print@InputForm[FullDefinition[sym]]]])
contextFreeDefinition[sym_Symbol, context_String] :=
contextFreeDefinition[sym, {context}]
contextFreeDefinition[sym_Symbol] :=
contextFreeDefinition[sym, commonestContexts[sym]]
справила []
Предостережение: эта функция не локализует переменные одинаково With а также Module do, что означает, что вложенные конструкции локализации не будут работать должным образом. withRules[{a -> 1, b -> 2}, With[{a=3}, b_ :> b]] заменит a а также b во вложенном With а также Rule, в то время как With не делает этого
Это вариант With который использует правила вместо = а также :=:
ClearAll[withRules]
SetAttributes[withRules, HoldAll]
withRules[rules_, expr_] :=
Internal`InheritedBlock[
{Rule, RuleDelayed},
SetAttributes[{Rule, RuleDelayed}, HoldFirst];
Unevaluated[expr] /. rules
]
Я нашел это полезным при очистке кода, написанного во время экспериментов и локализации переменных. Иногда я получаю списки параметров в виде {par1 -> 1.1, par2 -> 2.2}, С withRules Значения параметров легко внедрить в код, ранее написанный с использованием глобальных переменных.
Использование так же, как With:
withRules[
{a -> 1, b -> 2},
a+b
]
Сглаживание 3D-графики
Это очень простая техника для сглаживания трехмерной графики, даже если ваше графическое оборудование не поддерживает ее изначально.
antialias[g_, n_: 3] :=
ImageResize[Rasterize[g, "Image", ImageResolution -> n 72], Scaled[1/n]]
Вот пример:
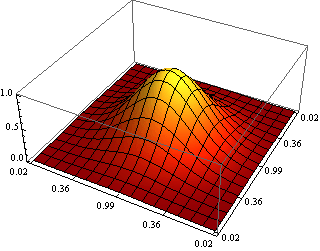
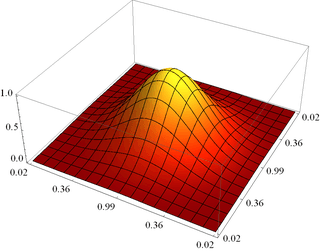
Обратите внимание, что большое значение для n или большой размер изображения имеет тенденцию выставлять ошибки графического драйвера или вносить артефакты.
Функциональность diff ноутбука
Функциональность diff ноутбука доступна в <<AuthorTools` пакет, и (по крайней мере, в версии 8) в недокументированном NotebookTools` контекст. Это небольшой графический интерфейс для отображения двух открытых на данный момент ноутбуков:
PaletteNotebook@DynamicModule[
{nb1, nb2},
Dynamic@Column[
{PopupMenu[Dynamic[nb1],
Thread[Notebooks[] -> NotebookTools`NotebookName /@ Notebooks[]]],
PopupMenu[Dynamic[nb2],
Thread[Notebooks[] -> NotebookTools`NotebookName /@ Notebooks[]]],
Button["Show differences",
CreateDocument@NotebookTools`NotebookDiff[nb1, nb2]]}]
]

Рекурсивные чистые функции (#0Кажется, один из самых темных уголков языка. Вот пара нетривиальных примеров их использования, где это действительно полезно (не то, что они не могут быть сделаны без него). Ниже приведена довольно краткая и достаточно быстрая функция для поиска связанных компонентов в графе, учитывая список ребер, заданных в виде пар вершин:
ClearAll[setNew, componentsBFLS];
setNew[x_, x_] := Null;
setNew[lhs_, rhs_]:=lhs:=Function[Null, (#1 := #0[##]); #2, HoldFirst][lhs, rhs];
componentsBFLS[lst_List] := Module[{f}, setNew @@@ Map[f, lst, {2}];
GatherBy[Tally[Flatten@lst][[All, 1]], f]];
Здесь происходит то, что мы сначала отображаем фиктивный символ на каждом из номеров вершин, а затем устанавливаем способ, который, учитывая пару вершин {f[5],f[10]}скажем тогда f[5] оценил бы f[10], Функция рекурсивной очистки используется в качестве компрессора пути (для настройки запоминания таким образом, чтобы вместо длинных цепочек типа f[1]=f[3],f[3]=f[4],f[4]=f[2], ...Записанные значения корректируются всякий раз, когда обнаруживается новый "корень" компонента. Это дает значительное ускорение. Поскольку мы используем присваивание, нам нужно, чтобы он был HoldAll, что делает эту конструкцию еще более непонятной и привлекательной). Эта функция является результатом дискуссий Mathgroup, в которых участвуют Фред Саймонс, Szabolcs Horvat, DrMajorBob и все остальные. Пример:
In[13]:= largeTest=RandomInteger[{1,80000},{40000,2}];
In[14]:= componentsBFLS[largeTest]//Short//Timing
Out[14]= {0.828,{{33686,62711,64315,11760,35384,45604,10212,52552,63986,
<<8>>,40962,7294,63002,38018,46533,26503,43515,73143,5932},<<10522>>}}
Это, конечно, намного медленнее, чем встроенный, но по размеру кода, все еще довольно быстрый IMO.
Другой пример: вот рекурсивная реализация Selectна основе связанных списков и рекурсивных чистых функций:
selLLNaive[x_List, test_] :=
Flatten[If[TrueQ[test[#1]],
{#1, If[#2 === {}, {}, #0 @@ #2]},
If[#2 === {}, {}, #0 @@ #2]] & @@ Fold[{#2, #1} &, {}, Reverse[x]]];
Например,
In[5]:= Block[
{$RecursionLimit= Infinity},
selLLNaive[Range[3000],EvenQ]]//Short//Timing
Out[5]= {0.047,{2,4,6,8,10,12,14,16,18,20,22,24,26,28,30,
<<1470>>,2972,2974,2976,2978,2980,2982,2984,2986,2988,2990,
2992,2994,2996,2998,3000}}
Тем не менее, он не является хвостовой рекурсивом, и уничтожает стек (приводит к краху ядра) для больших списков. Вот хвосто-рекурсивная версия:
selLLTailRec[x_List, test_] :=
Flatten[
If[Last[#1] === {},
If[TrueQ[test[First[#1]]],
{#2, First[#1]}, #2],
(* else *)
#0[Last[#1],
If[TrueQ[test[First[#1]]], {#2, First[#1]}, #2]
]] &[Fold[{#2, #1} &, {}, Reverse[x]], {}]];
Например,
In[6]:= Block[{$IterationLimit= Infinity},
selLLTailRec[Range[500000],EvenQ]]//Short//Timing
Out[6]= {2.39,{2,4,6,8,10,12,14,16,18,20,22,
<<249978>>,499980,499982,499984,499986,499988,499990,499992,
499994,499996,499998,500000}}
Можно запустить MathKernel в пакетном режиме, используя недокументированные параметры командной строки -batchinput а также -batchoutput:
math -batchinput -batchoutput < input.m > outputfile.txt
(где input.m файл пакетного ввода, заканчивающийся символом новой строки, outputfile.txt это файл, в который будет перенаправлен вывод)
В Mathematica v.> = 6 MathKernel имеет недокументированный параметр командной строки:
-noicon
который контролирует, будет ли MathKernel иметь видимый значок на панели задач (по крайней мере, под Windows).
FrontEnd (по крайней мере из v.5) имеет недокументированный параметр командной строки
-b
который отключает заставку и позволяет намного быстрее запускать Mathematica FrontEnd
и вариант
-directlaunch
который отключает механизм запуска последней установленной версии Mathematica вместо запуска версии, связанной с файлами.nb в системном реестре.
Другой способ сделать это, вероятно, это:
Вместо запуска двоичного файла Mathematica.exe в установочном каталоге запустите двоичный файл Mathematica.exe в SystemFiles\FrontEnd\Binaries\Windows. Первая - это простая программа запуска, которая изо всех сил старается перенаправить запросы на открытие записных книжек для запуска копий пользовательского интерфейса. Последний является двоичным файлом пользовательского интерфейса.
Удобно сочетать последнюю опцию командной строки с настройкой глобальной опции FrontEnd VersionedPreferences->True который отключает обмен настройками между различными установленными версиями Mathematica:
SetOptions[$FrontEnd, VersionedPreferences -> True]
(Выше следует оценить в самой последней установленной версии Mathematica.)
С помощью недокументированного ключа можно получить неполный список параметров командной строки FrontEnd. -h (код для Windows):
SetDirectory[$InstallationDirectory <>
"\\SystemFiles\\FrontEnd\\Binaries\\Windows\\"];
Import["!Mathematica -h", "Text"]
дает:
Usage: Mathematica [options] [files]
Valid options:
-h (--help): prints help message
-cleanStart (--cleanStart): removes existing preferences upon startup
-clean (--clean): removes existing preferences upon startup
-nogui (--nogui): starts in a mode which is initially hidden
-server (--server): starts in a mode which disables user interaction
-activate (--activate): makes application frontmost upon startup
-topDirectory (--topDirectory): specifies the directory to search for resources and initialization files
-preferencesDirectory (--preferencesDirectory): specifies the directory to search for user AddOns and preference files
-password (--password): specifies the password contents
-pwfile (--pwfile): specifies the path for the password file
-pwpath (--pwpath): specifies the directory to search for the password file
-b (--b): launches without the splash screen
-min (--min): launches as minimized
Другие варианты включают в себя:
-directLaunch: force this FE to start
-32: force the 32-bit FE to start
-matchingkernel: sets the frontend to use the kernel of matching bitness
-Embedding: specifies that this instance is being used to host content out of process
Существуют ли другие потенциально полезные параметры командной строки MathKernel и FrontEnd? Пожалуйста, поделитесь, если знаете.
Это рецепт из книги Стэна Вагона... используйте его, когда встроенный график ведет себя хаотично из-за отсутствия точности
Options[PrecisePlot] = {PrecisionGoal -> 6};
PrecisePlot[f_, {x_, a_, b_}, opts___] := Module[{g, pg},
pg = PrecisionGoal /. {opts} /. Options[PrecisePlot];
SetAttributes[g, NumericFunction];
g[z_?InexactNumberQ] := Evaluate[f /. x -> z];
Plot[N[g[SetPrecision[y, \[Infinity]]], pg], {y, a, b},
Evaluate[Sequence @@ FilterRules[{opts}, Options[Plot]]]]];
Я часто использую следующий трюк от Кристьяна Каннике, когда мне нужно "словарное" поведение из понижательных значений Mathematica
index[downvalue_,
dict_] := (downvalue[[1]] /. HoldPattern[dict[x_]] -> x) //
ReleaseHold;
value[downvalue_] := downvalue[[-1]];
indices[dict_] :=
Map[#[[1]] /. {HoldPattern[dict[x_]] -> x} &, DownValues[dict]] //
ReleaseHold;
values[dict_] := Map[#[[-1]] &, DownValues[dict]];
items[dict_] := Map[{index[#, dict], value[#]} &, DownValues[dict]];
indexQ[dict_, index_] :=
If[MatchQ[dict[index], HoldPattern[dict[index]]], False, True];
(* Usage example: *)
(* Count number of times each subexpression occurs in an expression *)
expr = Cos[x + Cos[Cos[x] + Sin[x]]] + Cos[Cos[x] + Sin[x]]
Map[(counts[#] = If[indexQ[counts, #], counts[#] + 1, 1]; #) &, expr, Infinity];
items[counts]
Когда результаты оценки сбивают с толку, иногда это помогает записать шаги оценки в текстовый файл
SetAttributes[recordSteps, HoldAll];
recordSteps[expr_] :=
Block[{$Output = List@OpenWrite["~/temp/msgStream.m"]},
TracePrint[Unevaluated[expr], _?(FreeQ[#, Off] &),
TraceInternal -> True];
Close /@ $Output;
Thread[Union@
Cases[ReadList["~/temp/msgStream.m", HoldComplete[Expression]],
symb_Symbol /;
AtomQ@Unevaluated@symb &&
Context@Unevaluated@symb === "System`" :>
HoldComplete@symb, {0, Infinity}, Heads -> True], HoldComplete]
]
(* Usage example: *)
(* puts steps of evaluation of 1+2+Sin[5]) into ~/temp/msgStream.m *)
recordSteps[1+2+Sin[5]]
Мои любимые хаки - это небольшие макросы, генерирующие код, которые позволяют заменить набор стандартных шаблонных команд одной короткой. Кроме того, вы можете создавать команды для открытия / создания блокнотов.
Вот то, что я использовал некоторое время в своем повседневном рабочем процессе Mathematica. Я часто выполняю следующее:
- Сделайте блокнот закрытым, загрузите нужные мне пакеты, сделайте автосохранение.
- Поработав с этим блокнотом какое-то время, я бы хотел сделать несколько пустых вычислений в отдельном блокноте с собственным контекстом, имея доступ к определениям, которые я использовал в "основном" блокноте. Поскольку я настроил закрытый контекст, для этого необходимо вручную настроить $ContextPath
Делать все это вручную снова и снова - это боль, поэтому давайте автоматизировать! Сначала немного служебного кода:
(* Credit goes to Sasha for SelfDestruct[] *)
SetAttributes[SelfDestruct, HoldAllComplete];
SelfDestruct[e_] := (If[$FrontEnd =!= $Failed,
SelectionMove[EvaluationNotebook[], All, EvaluationCell];
NotebookDelete[]]; e)
writeAndEval[nb_,boxExpr_]:=(
NotebookWrite[nb, CellGroupData[{Cell[BoxData[boxExpr],"Input"]}]];
SelectionMove[nb, Previous, Cell];
SelectionMove[nb, Next, Cell];
SelectionEvaluate[nb];
)
ExposeContexts::badargs =
"Exposed contexts should be given as a list of strings.";
ExposeContexts[list___] :=
Module[{ctList}, ctList = Flatten@List@list;
If[! MemberQ[ctList, Except[_String]],AppendTo[$ContextPath, #] & /@ ctList,
Message[ExposeContexts::badargs]];
$ContextPath = DeleteDuplicates[$ContextPath];
$ContextPath]
Autosave[x:(True|False)] := SetOptions[EvaluationNotebook[],NotebookAutoSave->x];
Теперь давайте создадим макрос, который поместит в записную книжку следующие ячейки:
SetOptions[EvaluationNotebook[], CellContext -> Notebook]
Needs["LVAutils`"]
Autosave[True]
А вот и макрос:
MyPrivatize[exposedCtxts : ({__String} | Null) : Null]:=
SelfDestruct@Module[{contBox,lvaBox,expCtxtBox,assembledStatements,strList},
contBox = MakeBoxes[SetOptions[EvaluationNotebook[], CellContext -> Notebook]];
lvaBox = MakeBoxes[Needs["LVAutils`"]];
assembledStatements = {lvaBox,MakeBoxes[Autosave[True]],"(*********)"};
assembledStatements = Riffle[assembledStatements,"\[IndentingNewLine]"]//RowBox;
writeAndEval[InputNotebook[],contBox];
writeAndEval[InputNotebook[],assembledStatements];
If[exposedCtxts =!= Null,
strList = Riffle[("\"" <> # <> "\"") & /@ exposedCtxts, ","];
expCtxtBox = RowBox[{"ExposeContexts", "[", RowBox[{"{", RowBox[strList], "}"}], "]"}];
writeAndEval[InputNotebook[],expCtxtBox];
]
]
Теперь, когда я набираю MyPrivatize[] Это создает частный контекст и загружает мой стандартный пакет. Теперь давайте создадим команду, которая откроет новую блокнотную записку с собственным закрытым контекстом (так что вы можете взломать ее с полной непринужденностью без риска испортить определения), но иметь доступ к вашим текущим контекстам.
SpawnScratch[] := SelfDestruct@Module[{nb,boxExpr,strList},
strList = Riffle[("\"" <> # <> "\"") & /@ $ContextPath, ","];
boxExpr = RowBox[{"MyPrivatize", "[",
RowBox[{"{", RowBox[strList], "}"}], "]"}];
nb = CreateDocument[];
writeAndEval[nb,boxExpr];
]
Самое интересное в этом то, что из-за SelfDestructКогда команда запускается, она не оставляет следов в текущей записной книжке - что хорошо, потому что в противном случае она просто создала бы беспорядок.
Для дополнительных точек стиля вы можете создать триггеры ключевых слов для этих макросов, используя InputAutoReplacementsНо я оставлю это как упражнение для читателя.
Поместить приложение с PageWidth -> Infinity
В Mathematica использование PutAppend Команда - это самый простой способ сохранить работающий файл журнала с результатами промежуточных вычислений. Но он использует по умолчанию PageWith->78 настройка при экспорте выражений в файл, поэтому нет гарантии, что каждый промежуточный вывод займет только одну строку в журнале.
PutAppend Сам не имеет никаких вариантов, но отслеживание его оценок показывает, что оно основано на OpenAppend функция, которая имеет PageWith и позволяет изменить его значение по умолчанию SetOptions команда:
In[2]:= Trace[x>>>"log.txt",TraceInternal->True]
Out[2]= {x>>>log.txt,{OpenAppend[log.txt,CharacterEncoding->PrintableASCII],OutputStream[log.txt,15]},Null}
Таким образом, мы можем получить PutAppend добавить только одну строку за раз, установив:
SetOptions[OpenAppend, PageWidth -> Infinity]
ОБНОВИТЬ
В версии 10 появилась ошибка (исправлена в версии 11.3): SetOptions больше не влияет на поведение OpenWrite а также OpenAppend,
Обходной путь должен реализовать вашу собственную версию PutAppend с явным PageWidth -> Infinity опция:
Clear[myPutAppend]
myPutAppend[expr_, pathtofile_String] :=
(Write[#, expr]; Close[#];) &[OpenAppend[pathtofile, PageWidth -> Infinity]]
Обратите внимание, что мы также можем реализовать это через WriteString как показано в этом ответе, но в этом случае необходимо будет предварительно преобразовать выражение в соответствующее InputForm с помощью ToString[expr, InputForm],
Я просто просматривал один из своих пакетов для включения в него, и нашел несколько сообщений, которые я определил, что чудеса работы: Debug::<some name>, По умолчанию они отключены, поэтому не производят много накладных расходов. Но я могу засорять свой код ими и включать их, если мне нужно точно выяснить, как немного кода ведет себя.
Одна из вещей, которая беспокоит меня о встроенных ограничивающих конструкциях, заключается в том, что они оценивают все определения локальных переменных одновременно, поэтому вы не можете писать, например,
With[{a = 5, b = 2 * a},
...
]
Итак, некоторое время назад я придумал макрос под названием WithNest, который позволяет вам сделать это. Я нахожу это удобным, так как он позволяет вам хранить локальные привязки переменных без необходимости делать что-то вроде
Module[{a = 5,b},
b = 2 * a;
...
]
В конце концов, я смог найти лучший способ сделать это, используя специальный символ, чтобы облегчить повторение по списку привязок, и я поместил определение в его собственный пакет, чтобы этот символ был скрыт. Может быть, у кого-то есть более простое решение этой проблемы?
Если вы хотите попробовать это, поместите следующее в файл с именем Scoping.m:
BeginPackage["Scoping`"];
WithNest::usage=
"WithNest[{var1=val1,var2=val2,...},body] works just like With, except that
values are evaluated in order and later values have access to earlier ones.
For example, val2 can use var1 in its definition.";
Begin["`Private`"];
(* Set up a custom symbol that works just like Hold. *)
SetAttributes[WithNestHold,HoldAll];
(* The user-facing call. Give a list of bindings and a body that's not
our custom symbol, and we start a recursive call by using the custom
symbol. *)
WithNest[bindings_List,body:Except[_WithNestHold]]:=
WithNest[bindings,WithNestHold[body]];
(* Base case of recursive definition *)
WithNest[{},WithNestHold[body_]]:=body;
WithNest[{bindings___,a_},WithNestHold[body_]]:=
WithNest[
{bindings},
WithNestHold[With[List@a,body]]];
SyntaxInformation[WithNest]={"ArgumentsPattern"->{{__},_}};
SetAttributes[WithNest,{HoldAll,Protected}];
End[];
EndPackage[];
Этот код создает палитру, которая загружает выделение в Stack Exchange как изображение. В Windows предусмотрена дополнительная кнопка, которая обеспечивает более точную визуализацию выбора.
Скопируйте код в ячейку ноутбука и оцените. Затем выведите палитру из вывода и установите ее, используя Palettes -> Install Palette...
Если у вас есть какие-либо проблемы, оставьте комментарий здесь. Скачать версию для ноутбука можно здесь.
Begin["SOUploader`"];
Global`palette = PaletteNotebook@DynamicModule[{},
Column[{
Button["Upload to SE",
With[{img = rasterizeSelection1[]},
If[img === $Failed, Beep[], uploadWithPreview[img]]],
Appearance -> "Palette"],
If[$OperatingSystem === "Windows",
Button["Upload to SE (pp)",
With[{img = rasterizeSelection2[]},
If[img === $Failed, Beep[], uploadWithPreview[img]]],
Appearance -> "Palette"],
Unevaluated@Sequence[]
]
}],
(* Init start *)
Initialization :>
(
stackImage::httperr = "Server returned respose code: `1`";
stackImage::err = "Server returner error: `1`";
stackImage[g_] :=
Module[
{getVal, url, client, method, data, partSource, part, entity,
code, response, error, result},
getVal[res_, key_String] :=
With[{k = "var " <> key <> " = "},
StringTrim[
First@StringCases[
First@Select[res, StringMatchQ[#, k ~~ ___] &],
k ~~ v___ ~~ ";" :> v],
"'"]
];
data = ExportString[g, "PNG"];
JLink`JavaBlock[
url = "http://stackru.com/upload/image";
client =
JLink`JavaNew["org.apache.commons.httpclient.HttpClient"];
method =
JLink`JavaNew[
"org.apache.commons.httpclient.methods.PostMethod", url];
partSource =
JLink`JavaNew[
"org.apache.commons.httpclient.methods.multipart.\
ByteArrayPartSource", "mmagraphics.png",
JLink`MakeJavaObject[data]@toCharArray[]];
part =
JLink`JavaNew[
"org.apache.commons.httpclient.methods.multipart.FilePart",
"name", partSource];
part@setContentType["image/png"];
entity =
JLink`JavaNew[
"org.apache.commons.httpclient.methods.multipart.\
MultipartRequestEntity", {part}, method@getParams[]];
method@setRequestEntity[entity];
code = client@executeMethod[method];
response = method@getResponseBodyAsString[];
];
If[code =!= 200, Message[stackImage::httperr, code];
Return[$Failed]];
response = StringTrim /@ StringSplit[response, "\n"];
error = getVal[response, "error"];
result = getVal[response, "result"];
If[StringMatchQ[result, "http*"],
result,
Message[stackImage::err, error]; $Failed]
];
stackMarkdown[g_] :=
"";
stackCopyMarkdown[g_] := Module[{nb, markdown},
markdown = Check[stackMarkdown[g], $Failed];
If[markdown =!= $Failed,
nb = NotebookCreate[Visible -> False];
NotebookWrite[nb, Cell[markdown, "Text"]];
SelectionMove[nb, All, Notebook];
FrontEndTokenExecute[nb, "Copy"];
NotebookClose[nb];
]
];
(* Returns available vertical screen space,
taking into account screen elements like the taskbar and menu *)
screenHeight[] := -Subtract @@
Part[ScreenRectangle /. Options[$FrontEnd, ScreenRectangle],
2];
uploadWithPreview[img_Image] :=
CreateDialog[
Column[{
Style["Upload image to the Stack Exchange network?", Bold],
Pane[
Image[img, Magnification -> 1], {Automatic,
Min[screenHeight[] - 140, 1 + ImageDimensions[img][[2]]]},
Scrollbars -> Automatic, AppearanceElements -> {},
ImageMargins -> 0
],
Item[
ChoiceButtons[{"Upload and copy MarkDown"}, \
{stackCopyMarkdown[img]; DialogReturn[]}], Alignment -> Right]
}],
WindowTitle -> "Upload image to Stack Exchange?"
];
(* Multiplatform, fixed-width version.
The default max width is 650 to fit Stack Exchange *)
rasterizeSelection1[maxWidth_: 650] :=
Module[{target, selection, image},
selection = NotebookRead[SelectedNotebook[]];
If[MemberQ[Hold[{}, $Failed, NotebookRead[$Failed]], selection],
$Failed, (* There was nothing selected *)
target =
CreateDocument[{}, WindowSelected -> False, Visible -> False,
WindowSize -> maxWidth];
NotebookWrite[target, selection];
image = Rasterize[target, "Image"];
NotebookClose[target];
image
]
];
(* Windows-only pixel perfect version *)
rasterizeSelection2[] :=
If[
MemberQ[Hold[{}, $Failed, NotebookRead[$Failed]],
NotebookRead[SelectedNotebook[]]],
$Failed, (* There was nothing selected *)
Module[{tag},
FrontEndExecute[
FrontEndToken[FrontEnd`SelectedNotebook[], "CopySpecial",
"MGF"]];
Catch[
NotebookGet@ClipboardNotebook[] /.
r_RasterBox :>
Block[{},
Throw[Image[First[r], "Byte", ColorSpace -> "RGB"], tag] /;
True];
$Failed,
tag
]
]
];
)
(* Init end *)
]
End[];
Этот был написан Альберто Ди Лулло (который, кажется, не в переполнении стека).
CopyToClipboard, для Mathematica 7 (в Mathematica 8 он встроен)
CopyToClipboard[expr_] :=
Module[{nb},
nb = CreateDocument[Null, Visible -> False, WindowSelected -> True];
NotebookWrite[nb, Cell[OutputFormData@expr], All];
FrontEndExecute[FrontEndToken[nb, "Copy"]];
NotebookClose@nb];
Оригинальный пост: http://forums.wolfram.com/mathgroup/archive/2010/Jun/msg00148.html
Я нашел эту процедуру полезной для копирования больших действительных чисел в буфер обмена в обычной десятичной форме. Например CopyToClipboard["123456789.12345"]
Cell[OutputFormData@expr] аккуратно удаляет цитаты.
Я уверен, что многие люди сталкивались с ситуацией, когда они запускали какой-то материал, понимая, что он не только зависал в программе, но и не сохранял последние 10 минут!
РЕДАКТИРОВАТЬ
Потерпев некоторое время от этого, я однажды узнал, что можно создать автосохранение из кода Mathematica. Я думаю, что использование такого автосохранения очень помогло мне в прошлом, и я всегда чувствовал, что сама возможность была чем-то, что не многие люди знают, что они могут сделать.
Оригинальный код, который я использовал, находится внизу. Благодаря комментариям я обнаружил, что это проблематично, и что гораздо лучше сделать это альтернативным способом, используя ScheduledTask (который будет работать только в Mathematica 8).
Код для этого можно найти в этом ответе от Sjoerd C. de Vries(Поскольку я не уверен, можно ли скопировать его сюда, я оставляю его только как ссылку.)
Решение ниже использует Dynamic, Он будет сохранять ноутбук каждые 60 секунд, но, видимо, только если его ячейка видна. Я оставляю это здесь только по причинам завершения. (и для пользователей Mathematica 6 и 7)
/РЕДАКТИРОВАТЬ
Чтобы решить это, я использую этот код в начале блокнота:
Dynamic[Refresh[NotebookSave[]; DateString[], UpdateInterval -> 60]]
Это сохранит вашу работу каждые 60 секунд.
Я предпочитаю это NotebookAutoSave[] потому что он сохраняет до обработки ввода и потому что некоторые файлы содержат больше текста, чем ввод.
Первоначально я нашел это здесь: http://en.wikipedia.org/wiki/Talk:Mathematica
Обратите внимание, что после запуска этой строки сохранение будет происходить, даже если вы закроете и снова откроете свой файл (если включено динамическое обновление).
Кроме того, поскольку в Mathematica нет отмены, будьте осторожны, чтобы не удалить весь ваш контент, поскольку сохранение сделает его необратимым (в качестве меры предосторожности я удаляю этот код из каждой законченной записной книжки)
Помните, что Книга Mathematica также доступна в Интернете по адресу http://reference.wolfram.com/legacy/v5_2/ хотя она заменена текущей документацией по адресу http://reference.wolfram.com/
Я считаю очень полезным при разработке пакетов добавлять этот ярлык клавиатуры в мой SystemFiles/FrontEnd/TextResources/Windows/KeyEventTranslations.tr файл.
(* Evaluate Initialization Cells: Real useful for reloading library changes. *)
Item[KeyEvent["i", Modifiers -> {Control, Command}],
FrontEndExecute[
FrontEndToken[
SelectedNotebook[],
"EvaluateInitialization"]]],
Далее за каждый Packagename.m Я делаю PackagenameTest.nb Записная книжка для тестирования и первые 2 ячейки тестовой записной книжки устанавливаются как ячейки инициализации. В первую ячейку я положил
Needs["PackageManipulations`"]
загрузить очень полезную библиотеку PackageManipulations, написанную Леонидом. Вторая ячейка содержит
PackageRemove["Packagename`Private`"]
PackageRemove["Packagename`"]
PackageReload["Packagename`"]
которые все делают фактическую перезагрузку пакета. Обратите внимание, что первые две строки существуют только для Remove все символы, которые мне нравятся, чтобы контексты были как можно более чистыми.
Тогда рабочий процесс для написания и тестирования пакета становится примерно таким.
- Сохранить изменения в
Packagename.m, - Идти к
PackagenameTest.nbи делатьCTRL + ALT + i,
Это заставляет ячейки инициализации перезагружать пакет, что делает тестирование очень простым.
Следующая функция format[expr_] может использоваться для отступа / форматирования неформатированного mathematica выражения, которые охватывают страницу
indent[str_String, ob_String, cb_String, delim_String] :=
Module[{ind, indent, f, tab}, ind = 0; tab = " ";
indent[i_, tab_, nl_] := nl <> Nest[tab <> ToString[#] &, "", i];
f[c_] := (indent[ind, "", " "] <> c <> indent[++ind, tab, "\n"]) /;StringMatchQ[ob, ___ ~~ c ~~ ___];
f[c_] := (indent[--ind, "", " "] <> c <> indent[ind, tab, "\n"]) /;StringMatchQ[cb, ___ ~~ c ~~ ___];
f[c_] := (c <> indent[ind, tab, "\n"]) /;StringMatchQ[delim, ___ ~~ c ~~ ___];
f[c_] := c;
f /@ Characters@str // StringJoin];
format[expr_] := indent[expr // InputForm // ToString, "[({", "])}", ";"];
(*
format[Hold@Module[{ind, indent, f, tab}, ind = 0; tab = " ";
indent[i_, tab_, nl_] := nl <> Nest[tab <> ToString[#] &, "", i];
f[c_] := (indent[ind, "", " "] <> c <> indent[++ind, tab, "\n"]) /;StringMatchQ[ob, ___ ~~ c ~~ ___];
f[c_] := (indent[--ind, "", " "] <> c <> indent[ind, tab, "\n"]) /;StringMatchQ[cb, ___ ~~ c ~~ ___];
f[c_] := (c <> indent[ind, tab, "\n"]) /;StringMatchQ[delim, ___ ~~ c ~~ ___];
f[c_] := c;
f /@ Characters@str // StringJoin]]
*)
ссылка: https://codegolf.stackexchange.com/questions/3088/indent-a-string-using-given-parentheses