Совпадение набора x,y указывает на другой набор, который масштабируется, поворачивается, переводится и с отсутствующими элементами
(Почему я это делаю? См. Объяснение ниже)
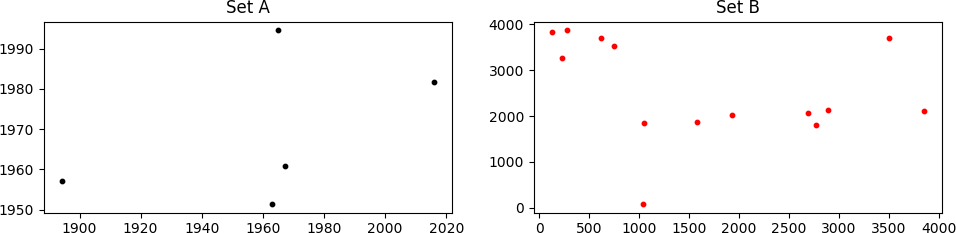
Рассмотрим два набора точек, A а также B как показано ниже
Это может выглядеть не так, но установить A "спрятан" в наборе B, Это не легко увидеть, потому что точки в B масштабируются, поворачиваются и переводятся в (x, y) в отношении A, Еще хуже, некоторые моменты, которые присутствуют в A отсутствуют в B, а также B содержит много точек, которые не находятся в A,
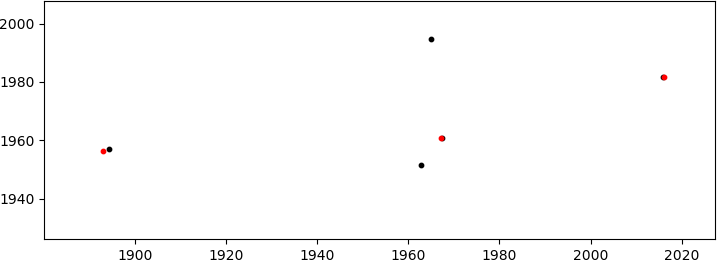
Мне нужно найти соответствующее масштабирование, вращение и перевод, которые должны быть применены к B установить, чтобы сопоставить его с множеством A, В случае, показанном выше, правильные значения:
scale = 0.14, rot_angle = 0.0, x_transl = 35.0, y_transl = 2.0
который производит (достаточно хорошее) совпадение
(в красном, только в соответствии B точки показаны; они расположены в секторе 1000<x<2000, y~2000 на первом рисунке справа). Учитывая много степеней свободы (DoF: масштабирование + вращение + 2D-перевод), я знаю о возможности несоответствия, но координаты точек не случайны (хотя они могут выглядеть так), поэтому вероятность этого происходит очень мало.
Код, который я написал (см. Ниже), использует грубую силу для обхода всех возможных значений DoF, взятых из предопределенных диапазонов для каждого. Ядро кода основано на минимизации расстояния каждой точки в A в любой момент B
Код работает (на самом деле он сгенерировал решение, упомянутое выше), но, поскольку количество решений (т. Е. Комбинаций принятых значений для каждого DoF) масштабируется с большими диапазонами, он может стать неприемлемо медленным довольно быстро (также он съедает все Оперативка в моей системе)
Как я могу улучшить производительность кода? Я открыт для любого решения, включая numpy и / или scipy, Возможно, что-то вроде Basing-Hopping для поиска лучшего соответствия (или относительно близкого) вместо метода грубой силы, который я сейчас использую?
import numpy as np
from scipy.spatial import distance
import math
def scalePoints(B_center, delta_x, delta_y, scale):
"""
Scales xy points.
http://codereview.stackexchange.com/q/159183/35351
"""
x_scale = B_center[0] - scale * delta_x
y_scale = B_center[1] - scale * delta_y
return x_scale, y_scale
def rotatePoints(center, x, y, angle):
"""
Rotates points in 'xy' around 'center'. Angle is in degrees.
Rotation is counter-clockwise
http://stackru.com/a/20024348/1391441
"""
angle = math.radians(angle)
xy_rot = x - center[0], y - center[1]
xy_rot = (xy_rot[0] * math.cos(angle) - xy_rot[1] * math.sin(angle),
xy_rot[0] * math.sin(angle) + xy_rot[1] * math.cos(angle))
xy_rot = xy_rot[0] + center[0], xy_rot[1] + center[1]
return xy_rot
def distancePoints(set_A, x_transl, y_transl):
"""
Find the sum of the minimum distance of points in set_A to points in set_B.
"""
d = distance.cdist(set_A, zip(*[x_transl, y_transl]), 'euclidean')
# Sum of all minimal distances.
d_sum = np.sum(np.min(d, axis=1))
return d_sum
def match_frames(
set_A, B_center, delta_x, delta_y, tol, sc_min, sc_max, sc_step,
ang_min, ang_max, ang_step, xmin, xmax, xstep, ymin, ymax, ystep):
"""
Process all possible solutions in the defined ranges.
"""
N = len(set_A)
# Ranges
sc_range = np.arange(sc_min, sc_max, sc_step)
ang_range = np.arange(ang_min, ang_max, ang_step)
x_range = np.arange(xmin, xmax, xstep)
y_range = np.arange(ymin, ymax, ystep)
print("Total solutions: {:.2e}".format(
np.prod([len(_) for _ in [sc_range, ang_range, x_range, y_range]])))
d_sum, params_all = [], []
for scale in sc_range:
# Scaled points.
x_scale, y_scale = scalePoints(B_center, delta_x, delta_y, scale)
for ang in ang_range:
# Rotated points.
xy_rot = rotatePoints(B_center, x_scale, y_scale, ang)
# x translation
for x_tr in x_range:
x_transl = xy_rot[0] + x_tr
# y translation
for y_tr in y_range:
y_transl = xy_rot[1] + y_tr
# Find minimum distance sum.
d_sum.append(distancePoints(set_A, x_transl, y_transl))
# Store solutions.
params_all.append([scale, ang, x_tr, y_tr])
# Condition to break out if given tolerance for match
# is achieved.
if d_sum[-1] <= tol * N:
print("Match found:", scale, ang, x_tr, y_tr)
i_min = d_sum.index(min(d_sum))
return i_min, params_all
# Print best solution found so far.
i_min = d_sum.index(min(d_sum))
print("d_sum_min = {:.2f}".format(d_sum[i_min]))
return i_min, params_all
# Data.
set_A = [[2015.81, 1981.665], [1967.31, 1960.865], [1962.91, 1951.365],
[1964.91, 1994.565], [1894.41, 1957.065]]
set_B = [
[2689.28, 3507.04, 2895.67, 1051.3, 1929.49, 1035.97, 752.44, 130.62,
620.06, 2769.06, 1580.77, 281.76, 224.54, 3848.3],
[2061.19, 3700.27, 2131.2, 1837.3, 2017.52, 80.96, 3524.61, 3821.22,
3711.53, 1812.12, 1868.33, 3865.77, 3273.77, 2100.71]]
# This is necessary to apply the scaling.
x, y = np.asarray(set_B)
# Center of B points, defined as the center of the minimal rectangle that
# contains all points.
B_center = [(min(x) + max(x)) * .5, (min(y) + max(y)) * .5]
# Difference between the center coordinates and the xy points.
delta_x, delta_y = B_center[0] - x, B_center[1] - y
# Tolerance in pixels for match.
tol = 1.
# Ranges for each DoF.
sc_min, sc_max, sc_step = .01, .2, .01
ang_min, ang_max, ang_step = -30., 30., 1.
xmin, xmax, xstep = -150., 150., 1.
ymin, ymax, ystep = -150., 150., 1.
# Find proper scaling + rotation + translation for set_B.
i_min, params_all = match_frames(
set_A, B_center, delta_x, delta_y, tol, sc_min, sc_max, sc_step,
ang_min, ang_max, ang_step, xmin, xmax, xstep, ymin, ymax, ystep)
# Best match found
print(params_all[i_min])
Почему я это делаю?
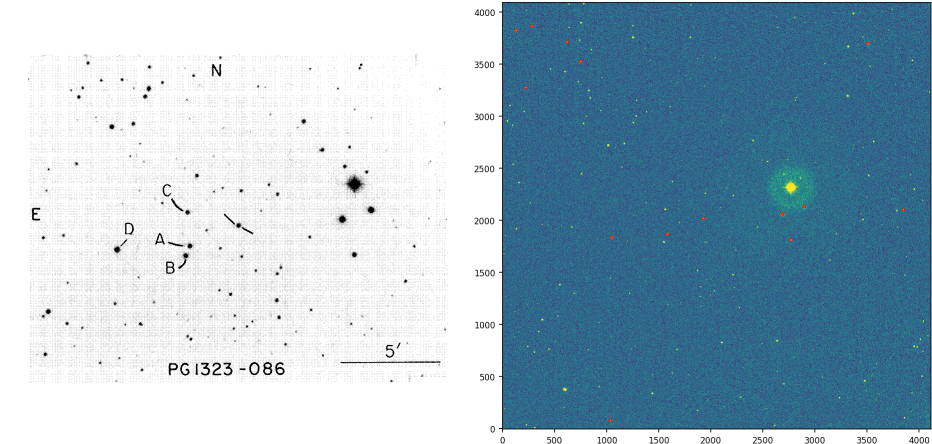
Когда астроном наблюдает звездное поле, ему также необходимо наблюдать то, что называется "стандартным полем звезд". Это необходимо для того, чтобы можно было преобразовать "инструментальные величины" (логарифмическая мера яркости) наблюдаемых звезд в общий универсальный масштаб, поскольку эти величины зависят от используемой оптической системы (телескоп + матрица ПЗС). В показанном здесь примере стандартное поле видно ниже слева, а наблюдаемое - справа.
Обратите внимание, что точки в наборе A (используется выше) - отмеченные звезды в стандартном поле и набор B те звезды, обнаруженные в наблюдаемом поле (отмечены красным выше)
Процесс идентификации тех звезд в наблюдаемом поле, которые соответствуют звездам, отмеченным в стандартном поле, выполняется на глаз, даже сегодня. Это связано со сложностью задачи.
На наблюдаемом изображении выше, есть немного масштабирования, но нет вращения и небольшого перемещения. Это довольно благоприятный сценарий; это может быть намного хуже. Я пытаюсь разработать простой алгоритм, чтобы избежать необходимости вручную идентифицировать звезды в наблюдаемом поле как звезды в стандартном поле, одну за другой.
Решение, предлагаемое litepresence
Это сценарий, который я сделал после ответа от litepresence.
import itertools
import numpy as np
import matplotlib.pyplot as plt
def getTriangles(set_X, X_combs):
"""
Inefficient way of obtaining the lengths of each triangle's side.
Normalized so that the minimum length is 1.
"""
triang = []
for p0, p1, p2 in X_combs:
d1 = np.sqrt((set_X[p0][0] - set_X[p1][0]) ** 2 +
(set_X[p0][1] - set_X[p1][1]) ** 2)
d2 = np.sqrt((set_X[p0][0] - set_X[p2][0]) ** 2 +
(set_X[p0][1] - set_X[p2][1]) ** 2)
d3 = np.sqrt((set_X[p1][0] - set_X[p2][0]) ** 2 +
(set_X[p1][1] - set_X[p2][1]) ** 2)
d_min = min(d1, d2, d3)
d_unsort = [d1 / d_min, d2 / d_min, d3 / d_min]
triang.append(sorted(d_unsort))
return triang
def sumTriangles(A_triang, B_triang):
"""
For each normalized triangle in A, compare with each normalized triangle
in B. find the differences between their sides, sum their absolute values,
and select the two triangles with the smallest sum of absolute differences.
"""
tr_sum, tr_idx = [], []
for i, A_tr in enumerate(A_triang):
for j, B_tr in enumerate(B_triang):
# Absolute value of lengths differences.
tr_diff = abs(np.array(A_tr) - np.array(B_tr))
# Sum the differences
tr_sum.append(sum(tr_diff))
tr_idx.append([i, j])
# Index of the triangles in A and B with the smallest sum of absolute
# length differences.
tr_idx_min = tr_idx[tr_sum.index(min(tr_sum))]
A_idx, B_idx = tr_idx_min[0], tr_idx_min[1]
print("Smallest difference: {}".format(min(tr_sum)))
return A_idx, B_idx
# Data.
set_A = [[2015.81, 1981.665], [1967.31, 1960.865], [1962.91, 1951.365],
[1964.91, 1994.565], [1894.41, 1957.065]]
set_B = [
[2689.28, 3507.04, 2895.67, 1051.3, 1929.49, 1035.97, 752.44, 130.62,
620.06, 2769.06, 1580.77, 281.76, 224.54, 3848.3],
[2061.19, 3700.27, 2131.2, 1837.3, 2017.52, 80.96, 3524.61, 3821.22,
3711.53, 1812.12, 1868.33, 3865.77, 3273.77, 2100.71]]
set_B = zip(*set_B)
# All possible triangles.
A_combs = list(itertools.combinations(range(len(set_A)), 3))
B_combs = list(itertools.combinations(range(len(set_B)), 3))
# Obtain normalized triangles.
A_triang, B_triang = getTriangles(set_A, A_combs), getTriangles(set_B, B_combs)
# Index of the A and B triangles with the smallest difference.
A_idx, B_idx = sumTriangles(A_triang, B_triang)
# Indexes of points in A and B of the best match triangles.
A_idx_pts, B_idx_pts = A_combs[A_idx], B_combs[B_idx]
print 'triangle A %s matches triangle B %s' % (A_idx_pts, B_idx_pts)
# Matched points in A and B.
print "A:", [set_A[_] for _ in A_idx_pts]
print "B:", [set_B[_] for _ in B_idx_pts]
# Plot
A_pts = zip(*[set_A[_] for _ in A_idx_pts])
B_pts = zip(*[set_B[_] for _ in B_idx_pts])
plt.scatter(*A_pts, s=10, c='k')
plt.scatter(*B_pts, s=10, c='r')
plt.show()
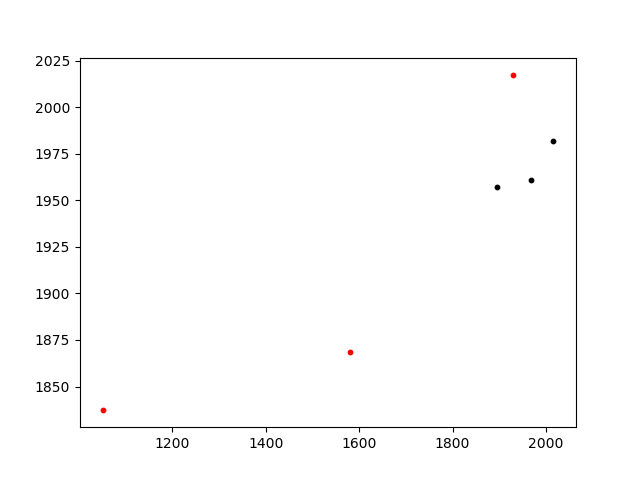
Метод почти мгновенный и дает правильное совпадение:
Smallest difference: 0.0314154749597
triangle A (0, 1, 4) matches triangle B (3, 4, 10)
A: [[2015.81, 1981.665], [1967.31, 1960.865], [1894.41, 1957.065]]
B: [(1051.3, 1837.3), (1929.49, 2017.52), (1580.77, 1868.33)]
2 ответа
1) Я бы подошел к этой проблеме, пометив все точки и найдя все возможные комбинации по 3 точки из каждого набора.
# normalize B data to same format as A
set_Bx, set_By = (set_B)
set_B = []
for i in range(len(set_Bx)):
set_B.append([set_Bx[i],set_By[i]])
'''
set_B = [[2689.28, 2061.19], [3507.04, 3700.27], [2895.67, 2131.2],
[1051.3, 1837.3], [1929.49, 2017.52], [1035.97, 80.96], [752.44,
3524.61], [130.62, 3821.22], [620.06, 3711.53], [2769.06, 1812.12],
[1580.77, 1868.33], [281.76, 3865.77], [224.54, 3273.77], [3848.3,
2100.71]]
'''
list(itertools.combinations(range(len(set_A)), 3))
list(itertools.combinations(range(len(set_B)), 3))
Как сгенерировать все перестановки списка в Python
2) Для каждой трехточечной группы вычислите стороны соответствующего треугольника; повторяя процесс для группы A и группы B.
dist = sqrt( (x2 - x1)**2 + (y2 - y1)**2 )
Как мне найти расстояние между двумя точками?
3) Затем уменьшите соотношение сторон для каждой так, чтобы наименьшая сторона каждого треугольника была тогда равна 1; остальные стороны уменьшены в соответствующем соотношении.
В двух похожих треугольниках:
Периметры двух треугольников находятся в том же соотношении, что и стороны. Соответствующие стороны, медианы и высоты будут в том же соотношении.
http://www.mathopenref.com/similartrianglesparts.html
4) Наконец, для каждого треугольника из группы A сравните каждый треугольник из группы B с поэлементным вычитанием. Затем сложите полученные элементы и найдите треугольники из A и B с наименьшей суммой.
list(numpy.array(list1)-numpy.array(list2))
5) Даны сопоставленные треугольники; Поиск подходящего масштабирования, перевода и вращения должен быть относительно тривиальным с точки зрения CPU / RAM. 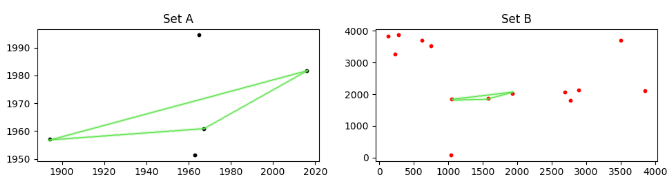
ETA1: черновик сценария
ETA2: исправленная ошибка, обсуждаемая в комментариях: с суммой (abs()) вместо abs(sum()). Теперь это работает, тоже быстро!
'''
known correct solution
A = [[1894.41, 1957.065],[1967.31, 1960.865],[2015.81, 1981.665]]
B = [[1051.3, 1837.3],[1580.77, 1868.33],[1929.49, 2017.52]]
'''
import numpy as np
import itertools
import math
import operator
set_A = [[2015.81, 1981.665], [1967.31, 1960.865], [1962.91, 1951.365],
[1964.91, 1994.565], [1894.41, 1957.065]]
set_B = [[2689.28, 3507.04, 2895.67, 1051.3, 1929.49, 1035.97, 752.44, 130.62,
620.06, 2769.06, 1580.77, 281.76, 224.54, 3848.3],
[2061.19, 3700.27, 2131.2, 1837.3, 2017.52, 80.96, 3524.61, 3821.22,
3711.53, 1812.12, 1868.33, 3865.77, 3273.77, 2100.71]]
# normalize set B data to set A format
set_Bx, set_By = (set_B)
set_B = []
for i in range(len(set_Bx)):
set_B.append([set_Bx[i],set_By[i]])
'''
set_B = [[2689.28, 2061.19], [3507.04, 3700.27], [2895.67, 2131.2],
[1051.3, 1837.3], [1929.49, 2017.52], [1035.97, 80.96], [752.44, 3524.61],
[130.62, 3821.22], [620.06, 3711.53], [2769.06, 1812.12], [1580.77, 1868.33],
[281.76, 3865.77], [224.54, 3273.77], [3848.3, 2100.71]]
'''
print set_A
print set_B
print len(set_A)
print len(set_B)
set_A_tri = list(itertools.combinations(range(len(set_A)), 3))
set_B_tri = list(itertools.combinations(range(len(set_B)), 3))
print set_A_tri
print set_B_tri
print len(set_A_tri)
print len(set_B_tri)
'''
set_A = [[2015.81, 1981.665], [1967.31, 1960.865], [1962.91, 1951.365],
[1964.91, 1994.565], [1894.41, 1957.065]]
set_A_tri = [(0, 1, 2), (0, 1, 3), (0, 1, 4), (0, 2, 3), (0, 2, 4), (0, 3, 4),
(1, 2, 3), (1, 2, 4), (1, 3, 4), (2, 3, 4)]
'''
def distance(x1,y1,x2,y2):
return math.sqrt((x2 - x1)**2 + (y2 - y1)**2 )
def tri_sides(set_x, set_x_tri):
triangles = []
for i in range(len(set_x_tri)):
point1 = set_x_tri[i][0]
point2 = set_x_tri[i][1]
point3 = set_x_tri[i][2]
point1x, point1y = set_x[point1][0], set_x[point1][1]
point2x, point2y = set_x[point2][0], set_x[point2][1]
point3x, point3y = set_x[point3][0], set_x[point3][1]
len1 = distance(point1x,point1y,point2x,point2y)
len2 = distance(point1x,point1y,point3x,point3y)
len3 = distance(point2x,point2y,point3x,point3y)
min_side = min(len1,len2,len3)
len1/=min_side
len2/=min_side
len3/=min_side
t=[len1,len2,len3]
t.sort()
triangles.append(t)
return triangles
A_triangles = tri_sides(set_A, set_A_tri)
B_triangles = tri_sides(set_B, set_B_tri)
print A_triangles
'''
[[1.0, 5.0405616860744304, 5.822935502560814],
[1.0, 1.5542012854321234, 1.5619803879976761],
[1.0, 1.3832883678507584, 2.347214708755337],
[1.0, 1.2141910838179129, 1.4096730529373076],
[1.0, 1.1275138587537166, 2.0318412465223665],
[1.0, 1.5207417600732074, 2.3589630093994876],
[1.0, 3.2270326342163584, 4.13069930678442],
[1.0, 6.565440477766354, 6.972550347780966],
[1.0, 2.1606693015281997, 2.3635387983160885],
[1.0, 1.589425903498476, 1.846471085870448]]
'''
print B_triangles
def list_subtract(list1,list2):
return np.absolute(np.array(list1)-np.array(list2))
sums = []
threshold = 1
for i in range(len(A_triangles)):
for j in range(len(B_triangles)):
k = sum(list_subtract(A_triangles[i], B_triangles[j]))
if k < threshold:
sums.append([i,j,k])
# sort by smallest sum
sums = sorted(sums, key=operator.itemgetter(2))
print sums
print 'winner %s' % sums[0]
print sums[0][0]
print sums[0][1]
match_A = set_A_tri[sums[0][0]]
match_B = set_B_tri[sums[0][1]]
print 'triangle A %s matches triangle B %s' % (match_A, match_B)
match_A_pts = []
match_B_pts = []
for i in range(3):
match_A_pts.append(set_A[match_A[i]])
match_B_pts.append(set_B[match_B[i]])
print 'triangle A has points %s' % match_A_pts
print 'triangle B has points %s' % match_B_pts
'''
winner [2, 204, 0.031415474959738399]
2
204
triangle A (0, 1, 4) matches triangle B (3, 4, 10)
triangle A has points [[2015.81, 1981.665], [1967.31, 1960.865], [1894.41, 1957.065]]
triangle B has points [[1051.3, 1837.3], [1929.49, 2017.52], [1580.77, 1868.33]]
'''
Существует алгоритм, называемый многомерным масштабированием, или MDS ( http://scikit-learn.org/stable/modules/generated/sklearn.manifold.MDS.html), который находит масштаб таких преобразований. Он тесно связан с анализом главных компонентов, но использует вектор линейных различий вместо ковариаций (которые являются своего рода квадратом различий).
Чтобы восстановить вращение и смещение, вы можете использовать RANSAC ( http://scikit-learn.org/stable/modules/generated/sklearn.linear_model.RANSACRegressor.html).