Нахождение кратчайшего расстояния между двумя параллельными линиями с произвольной точкой

Question

Мне нужно написать надежный метод, чтобы получить ответ на следующий сценарий...

Учитывая отрезок AB и произвольную точку C, как мне найти ближайшую точку к A на прямой, параллельной AB, которая проходит через точку C? (Надежность, упомянутая выше, относится к способности алгоритмов находить D, в то же время позволяя координатам A, B и C быть совершенно произвольными и непредсказуемыми. Я столкнулся с довольно многими решениями, которые я не смог адаптировать ко всем возможные сценарии, к сожалению...)

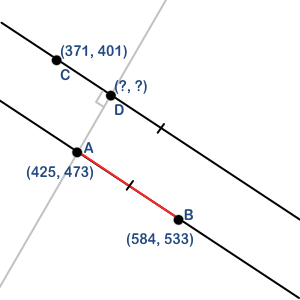
В случае данных, показанных на рисунке ниже, как я могу надежно найти координаты x,y точки D?

A = <425, 473>
B = <584, 533>
C = <371, 401>
D = <???, ???>

Зная, что AB и CD параллельны, это, очевидно, означает, что наклоны одинаковы.

Я пробовал много разных формул безрезультатно и работаю над этим уже несколько недель. Я в тупике!

Answer 1

Это проблема минимизации.

В общем, евклидово расстояние между двумя точками (A и B) в N-мерном пространстве определяется как Dist(A,B) = sqrt((A1-B1)^2 + ... + (AN-BN)^2)

Если вам нужно найти минимальное расстояние между пространственной кривой A(t) (одномерный объект, встроенный в некоторое N-мерное пространство) и точкой B, то вам нужно решить это уравнение:

d Dist(A(t),B) / dt = 0    // (this is straightforward calculus: we're at either a minimum or maximum when the rate of change is 0)

и проверить этот набор корней (t1, t2 и т. д.) по отношению к функции расстояния, чтобы найти, какая из них дает наименьшее значение D.

---

Теперь, чтобы найти уравнение для параллельной линии, проходящей через C, в виде y=mx+b:

m = (Ay - By)/(Ax-Bx)
b = Cy - mCx

Давайте напишем это в виде кривой пространства и вставим в нашу формулу из части 1:

Dist(D(t),A) = sqrt((t-Ax)^2 + (m*t+b-Ay)^2)

принимая нашу производную:

d Dist(D(t),A)/ dt = d sqrt((t-Ax)^2 + (m*t+b-Ay)^2) / dt 

= (t + (m^2)*t - Ax + m*b - m*Ay)/sqrt(t^2 + (m^2)t^2 - 2*t*Ax + 2*m*t*b - 2*m*t*Ay + (Ax)^2 + (Ay)^2 + b^2 - 2*b*Ay )
= ((1+m^2)*t - Ax + m*b - m*Ay)/sqrt((1+m^2)*(t^2)  + 2*t*(m*b - Ax - m*Ay) + (Ax)^2 + (Ay)^2 + b^2 - 2*b*Ay )

Установки равные 0 и решение для t дает: t = (Ax-m*b+m*Ay)/(1+m^2) в качестве единственного корня (вы можете проверить это сами, подставив обратно и проверив, что все отменяется по желанию).

Подстановка этого значения t обратно в нашу пространственную кривую дает следующее: D=<(Ax-m * b + m * Ay) / (1 + m ^ 2), b + m * (Ax-m * b + m * Ау) / (1 + т ^ 2)>

Затем вы можете вставить свои выражения для m и b, если хотите получить явное решение в терминах A,B,C или если вам нужно только численное решение, вы можете просто вычислить его как трехэтапный процесс:

m = (Ay - By)/(Ax-Bx)
b = Cy - mCx
D=<(Ax-m*b+m*Ay)/(1+m^2),b+m*(Ax-m*b+m*Ay)/(1+m^2)>

Это будет справедливо для всех случаев с параллельными прямыми. Одно предостережение при реализации его в виде числового (а не аналитического) кода: если линии ориентированы вертикально, вычисление m = (Ay-By)/(Ax-Bx) приведет к делению на 0, что сделает ваш код неработающим, Вы можете добавить предохранительный клапан следующим образом:

if( Ax == Bx) {
    D = <Cx,Ay>
} else {
    // normal calculation here
}

Для серьезной числовой работы вы, вероятно, захотите реализовать ее с точки зрения допусков, а не прямого сравнения из-за ошибок округления и всех этих забавных вещей (то есть abs(Ax-Bx)