GPFLow: получить полную ковариационную матрицу и найти ее энтропию

Question

Я хотел бы вычислить детерминант ковариационной матрицы регрессии GP в GPFlow. Я предполагаю, что смогу получить ковариационную матрицу с помощью этой функции:

GPModel.predict_f_full_cov

Эта функция была предложена здесь:

https://gpflow.readthedocs.io/en/develop/notebooks/regression.html

Тем не менее, я понятия не имею, как использовать эту функцию или что она возвращает. Мне нужно знать функцию, которая возвращает ковариационную матрицу для всей моей модели, а затем мне нужно знать, как вычислить ее определитель.

После некоторых усилий я выяснил, как дать завести gnate_f_full_cov в некоторые моменты, которые меня интересуют, как мы видим здесь:

c = m.predict_f_full_cov(np.array([[.2],[.4],[.6],[.8]])))

Это вернуло два массива, первый из которых является средним значением прогнозируемой функции для точек, которые я запрашивал вдоль оси x. Второй массив немного загадочный. Я предполагаю, что это ковариационная матрица. Я вытащил это, используя это:

covMatrix = m.predict_f_full_cov(np.array([[.2],[.4],[.6],[.8]]))[1][0]

Затем я посмотрел, как вычислить определитель, вот так:

x = np.linalg.det(covMatrix)

Затем я вычислил лог этого, чтобы получить энтропию для ковариационной матрицы:

print(-10*math.log(np.linalg.det(covMatrix)))

Я провел это дважды, используя два разных набора данных. У первого был высокий уровень шума, у второго - низкий уровень шума. Странно, но энтропия возросла для набора данных с меньшим уровнем шума. Я в растерянности.

Я обнаружил, что если я просто вычисляю ковариационную матрицу для небольшой области, которая должна быть линейной, то увеличение и уменьшение шума не дает ожидаемого результата. Кроме того, если я регрессирую GP к большому количеству пунктов, определитель идет к 0.0.

Вот код, который я использую:

import gpflow
import numpy as np
N = 300
noiseSize = 0.01
X = np.random.rand(N,1)
Y = np.sin(12*X) + 0.66*np.cos(25*X)  + np.random.randn(N,1)*noiseSize + 3
k = gpflow.kernels.Matern52(1, lengthscales=0.3)
m = gpflow.models.GPR(X, Y, kern=k)
m.likelihood.variance = 0.01
aRange = np.linspace(0.1,0.9,200)
newRange = []
for point in aRange:
    newRange.append([point])
covMatrix = m.predict_f_full_cov(newRange)[1][0]
import math
print("Determinant: " + str(np.linalg.det(covMatrix)))
print(-10*math.log(np.linalg.det(covMatrix)))

Answer 1

Итак, обо всем по порядку, энтропия многомерной нормали (и GP, учитывая фиксированный набор точек, по которым она оценивается) зависит только от ее ковариационной матрицы.

Ответы на ваши вопросы:

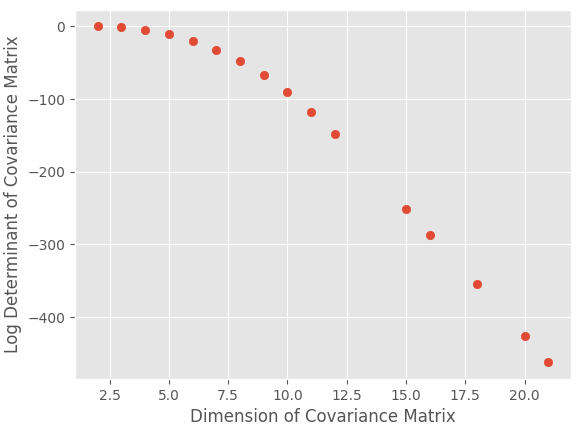
1. Да - когда вы делаете набор $X$ все более и более плотным, вы делаете ковариационную матрицу все больше и больше, и для многих простых ковариационных ядер это делает детерминант все меньше и меньше. Я предполагаю, что это связано с тем, что определители больших матриц имеют много слагаемых произведений (см. Формулу Лейбница), а произведения слагаемых меньше единицы стремятся к нулю быстрее, чем их суммы. Вы можете проверить это легко:

Код для этого:

import numpy as np
import matplotlib.pyplot as plt
import sklearn.gaussian_process.kernels as k

plt.style.use("ggplot"); plt.ion()

n = np.linspace(2, 25, 23, dtype = int)
d = np.zeros(len(n))

for i in range(len(n)):
    X = np.linspace(-1, 1, n[i]).reshape(-1, 1)
    S = k.RBF()(X)
    d[i] = np.log(np.linalg.det(S))

plt.scatter(n, d)
plt.ylabel("Log Determinant of Covariance Matrix")
plt.xlabel("Dimension of Covariance Matrix")

Прежде чем перейти к следующему пункту, обратите внимание, что энтропия многомерной нормали также имеет вклад от размера матрицы, поэтому, хотя определитель отходит до нуля, есть небольшой вклад от измерения.

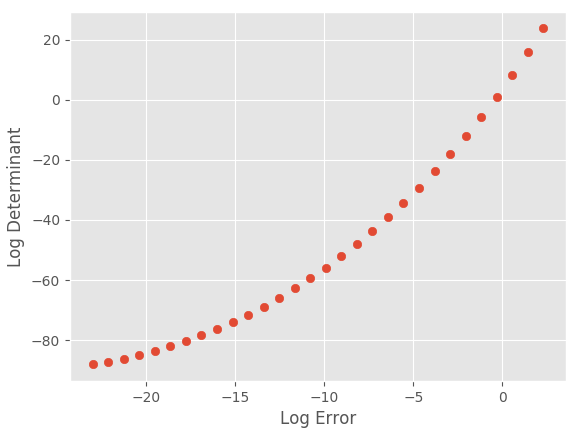
2. С уменьшением шума, как и следовало ожидать, энтропия и детерминант уменьшаются, но не стремятся к нулю точно; они уменьшатся до детерминанта из-за других ядер, присутствующих в ковариации. Для демонстрации ниже размер ковариации поддерживается постоянным ($10*10$), а уровень шума увеличивается с 0:

Код:

e = np.logspace(1, -10, 30)
d = np.zeros(len(e))
X = np.linspace(-1, 1, 10).reshape(-1, 1)

for i in range(len(e)):
    S = (k.RBF() + k.WhiteKernel(e[i])) (X)
    d[i] = np.log(np.linalg.det(S))

e = np.log(e)

plt.scatter(e, d)
plt.ylabel("Log Determinant")
plt.xlabel("Log Error")