Как конфертировать из NetworkX graph в ete3 Дерево объекта?

Question

Я пытаюсь выяснить, как построить ete3.Tree объект из networkx ориентированный граф? Я добавил каждый child так, как я думал, даст желаемый результат, но у меня проблемы.

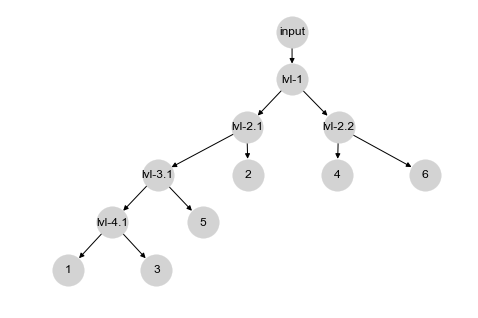
edges = [('lvl-1', 'lvl-2.1'), ('lvl-1', 'lvl-2.2'), ('lvl-2.1', 'lvl-3.1'), ('lvl-2.1', 2), ('lvl-2.2', 4), ('lvl-2.2', 6), ('lvl-3.1', 'lvl-4.1'), ('lvl-3.1', 5), ('lvl-4.1', 1), ('lvl-4.1', 3), ('input', 'lvl-1')]
graph = nx.OrderedDiGraph()
graph.add_edges_from(edges)
nx.draw(graph, pos=nx.nx_agraph.graphviz_layout(graph, prog="dot"), with_labels=True, node_size=1000, node_color="lightgray")

tree = ete3.Tree()
for parent, children in itertools.groupby(graph.edges(), lambda edge:edge[0]):
    subtree = ete3.Tree(name=parent)
    for child in children:
        subtree.add_child(name=child[1])
    tree.add_child(child=subtree, name=parent)
print(tree) 
#       /-lvl-2.1
#    /-|
#   |   \-lvl-2.2
#   |
#   |   /-lvl-3.1
#   |--|
#   |   \-2
#   |
#   |   /-4
#   |--|
# --|   \-6
#   |
#   |   /-lvl-4.1
#   |--|
#   |   \-5
#   |
#   |   /-1
#   |--|
#   |   \-3
#   |
#    \- /-lvl-1

Я также попробовал следующее, но это не сработало:

tree = ete3.Tree()
for parent, child in graph.edges():
    if parent not in tree:
        tree.add_child(name=parent)
    subtree = tree.search_nodes(name=parent)[0]
    subtree.add_child(name=child)
print(tree)
#                /-1
#             /-|
#          /-|   \-3
#         |  |
#       /-|   \-5
#      |  |
#    /-|   \-2
#   |  |
#   |  |   /-4
# --|   \-|
#   |      \-6
#   |
#    \- /-lvl-1

Answer 1

# Graph
edges = [('lvl-1', 'lvl-2.1'), ('lvl-1', 'lvl-2.2'), ('lvl-2.1', 'lvl-3.1'), ('lvl-2.1', 2), ('lvl-2.2', 4), ('lvl-2.2', 6), ('lvl-3.1', 'lvl-4.1'), ('lvl-3.1', 5), ('lvl-4.1', 1), ('lvl-4.1', 3), ('input', 'lvl-1')]
G = nx.OrderedDiGraph()
G.add_edges_from(edges)

# Tree
root = "input"
subtrees = {node:ete3.Tree(name=node) for node in G.nodes()}
[*map(lambda edge:subtrees[edge[0]].add_child(subtrees[edge[1]]), G.edges())]
tree = subtrees[root]
print(tree.get_ascii())
#                                /-1
#                         /lvl-4.1
#                  /lvl-3.1      \-3
#                 |      |
#           /lvl-2.1      \-5
#          |      |
# -inputlvl-1      \-2
#          |
#          |       /-4
#           \lvl-2.2
#                  \-6

Answer 2

С поддеревьями и чтением из объекта networkX все в порядке, проблема в том, что вы добавляете все поддеревья к своему оригиналу tree экземпляр напрямую. В ete3, Tree класс на самом деле является просто узлом (включая указатели на его потомков, если таковые имеются), поэтому tree.add_child добавляет новые дочерние узлы / поддеревья непосредственно в корневой узел.

Вместо этого вам нужно перебрать листья дерева ete, найти тот, где node.name == parent и приложите к нему всех детей. Кроме того, вы должны прикреплять их один за другим, а не предварительно генерировать поддерево. В противном случае вы получите дополнительный внутренний узел с одним родителем и одним ребенком.

РЕДАКТИРОВАТЬ:

Вторая версия вашего кода почти верна, но вы не учитываете, что узлы никогда не должны быть присоединены к дереву (то есть корню), если корень не является их фактическим родителем. Наверное, поэтому вы получаете lvl-1 как отдельный узел, который не является родителем других узлов. Кроме того, я не уверен насчет порядка обхода графа networkX, что может быть важно. Более безопасная (если более уродливая) версия будет выглядеть так:

# Setting up a root node for lvl-1 to attach to
tree.add_child(name='input')
# A copy in a list, because you may not want to edit the original graph
edges = list(graph.edges)
while len(edges) > 0:
    for parent, child in edges:
        # check if this edge's parent is in the tree
        for leaf it tree.get_leaves(): 
            if leaf.name == parent:
                # if it is, add child and thus create an edge
                leaf.add_child(name=child)
            # Wouldn't want to add the same edge twice, would you?
            edges.remove((parent, child))
    # Now if there are edges still unplaced, try again.

Там может быть несколько опечаток, и это определенно очень медленно. Что-то около O(n**2) из ​​числа ребер или хуже, что со всей итерацией и удалением списка. Вероятно, существует метод для перемещения графа от корня к листьям, для которого не потребуется копия списка ребер (и он будет работать за одну итерацию). Но это в конечном итоге даст правильное дерево.