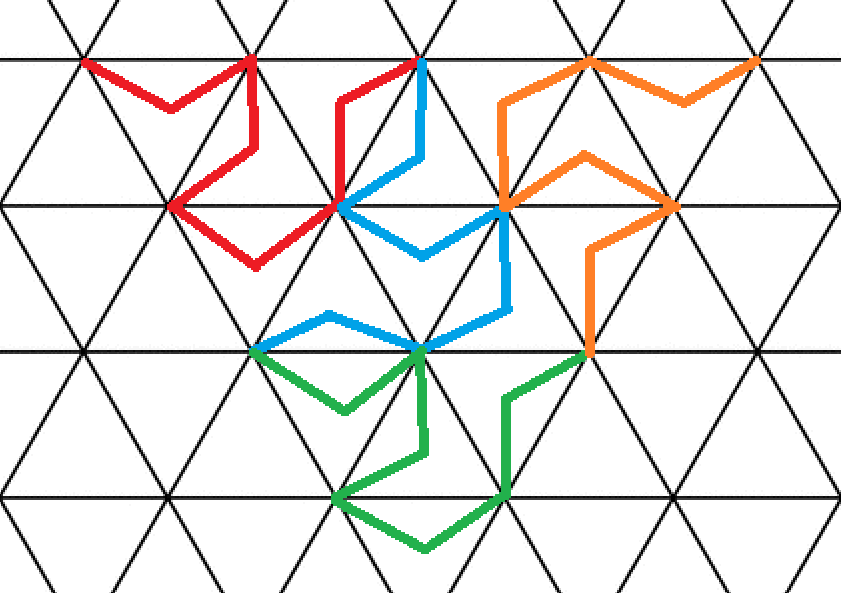
Каков эквивалент кривой Псевдо-Хилберта для гексогональных и треугольных тесселяций?
Треугольники, квадраты и шестиугольники могут быть использованы для заполнения поверхности (тесселяция).
А пока давайте предположим, что поверхность имеет ограниченное количество плиток (треугольников, квадратов или шестиугольников)
Цель состоит в том, чтобы определить линию, которая касается каждой плитки, так, чтобы точки, которые находятся близко друг к другу, или линия (1D) также были близки друг к другу на поверхности (2D).
Решение для квадратного тесселяции имеет кривую (Псевдо)-Гильберта. Ниже приведен пример кривой псевдо-Хилберта второго порядка.
Объяснено в этом фантастическом видео
Мне было интересно, каков эквивалент (если таковой имеется) псевдогильбертовой кривой для тесселяций, основанных на треугольниках или шестиугольниках. Я ищу полный тесселяции, чтобы не было дыр, как в треугольнике Серпинского.
Я нашел этот великий ресурс
А для треугольников используется кривая Пеано.