Когда целесообразно использовать поиск в глубину (DFS) по сравнению с поиском в ширину (BFS)?
Я понимаю разницу между DFS и BFS, но мне интересно знать, когда практичнее использовать один поверх другого?
Может ли кто-нибудь привести примеры того, как DFS превзойдет BFS и наоборот?
15 ответов
Это сильно зависит от структуры дерева поиска, а также от количества и местоположения решений (так называемых искомых элементов).
- Если вы знаете, что решение находится недалеко от корня дерева, поиск в ширину (BFS) может быть лучше.
Если дерево очень глубокое и решения встречаются редко, поиск в глубину (DFS) может занять очень много времени, но BFS может быть быстрее.
Если дерево очень широкое, BFS может потребоваться слишком много памяти, поэтому оно может быть совершенно непрактичным.
Если решения часто, но расположены глубоко в дереве, BFS может быть непрактичным.
- Если дерево поиска очень глубокое, вам все равно придется ограничить глубину поиска для поиска в глубину (DFS) (например, с итеративным углублением).
Но это всего лишь эмпирические правила; вам, вероятно, нужно будет поэкспериментировать.
Поиск в глубину
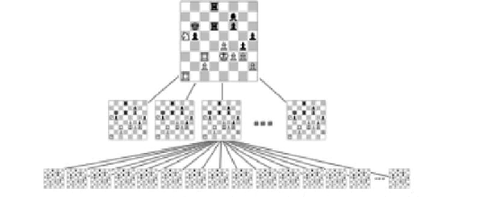
Поиск в глубину часто используется при моделировании игр (и игровых ситуаций в реальном мире). В типичной игре вы можете выбрать одно из нескольких возможных действий. Каждый выбор ведет к дальнейшему выбору, каждый из которых ведет к дальнейшему выбору, и так далее, в постоянно расширяющийся древовидный график возможностей.
Например, в таких играх, как шахматы, крестики-нолики, когда вы решаете, какой шаг сделать, вы можете мысленно представить себе ход, затем возможные ответы противника, затем ваши ответы и так далее. Вы можете решить, что делать, видя, какой шаг приводит к наилучшему результату.
Только некоторые пути в игровом дереве ведут к вашей победе. Некоторые из них приводят к победе вашего противника, когда вы достигаете такого конца, вы должны вернуться назад или вернуться к предыдущему узлу и попробовать другой путь. Таким образом, вы исследуете дерево, пока не найдете путь с успешным завершением. Затем вы делаете первый шаг по этому пути.
Поиск в ширину
Поиск в ширину имеет интересное свойство: сначала он находит все вершины, которые находятся на расстоянии одного ребра от начальной точки, затем все вершины, которые находятся на расстоянии двух ребер, и так далее. Это полезно, если вы пытаетесь найти кратчайший путь от начальной вершины до данной вершины. Вы запускаете BFS, и когда вы находите указанную вершину, вы знаете, что путь, который вы проследили до сих пор, является кратчайшим путем к узлу. Если бы был более короткий путь, BFS уже нашла бы его.
Поиск в ширину можно использовать для поиска соседних узлов в одноранговых сетях, таких как BitTorrent, системы GPS для поиска близлежащих мест, сайты социальных сетей для поиска людей на указанном расстоянии и тому подобное.
Хорошее объяснение с http://www.programmerinterview.com/index.php/data-structures/dfs-vs-bfs/
Пример БФС
Вот пример того, как будет выглядеть BFS. Это что-то вроде обхода дерева порядка уровней, когда мы будем использовать QUEUE с подходом ITERATIVE (в основном, RECURSION будет заканчиваться DFS). Числа представляют порядок, в котором к узлам обращаются в BFS:
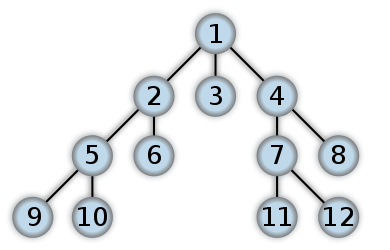
При глубоком поиске вы начинаете с корня и следите за одной из ветвей дерева, насколько это возможно, до тех пор, пока не будет найден искомый узел или вы не достигнете листового узла (узла без дочерних элементов). Если вы нажмете на листовой узел, вы продолжите поиск у ближайшего предка с неисследованными детьми.
Пример ДФС
Вот пример того, как будет выглядеть DFS. Я думаю, что обратный порядок в двоичном дереве сначала начнет работать с уровня Leaf. Числа представляют порядок, в котором к узлам обращаются в DFS:
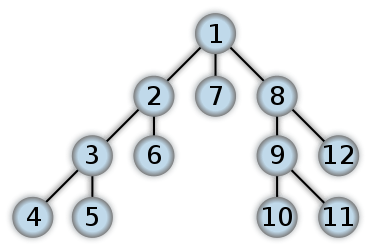
Различия между DFS и BFS
Сравнивая BFS и DFS, большим преимуществом DFS является то, что он имеет гораздо более низкие требования к памяти, чем BFS, поскольку нет необходимости хранить все дочерние указатели на каждом уровне. В зависимости от данных и того, что вы ищете, может быть полезен DFS или BFS.
Например, с учетом генеалогического дерева, если кто-то ищет на дереве того, кто еще жив, тогда можно было бы с уверенностью предположить, что этот человек будет на дне дерева. Это означает, что BFS потребуется очень много времени, чтобы достичь этого последнего уровня. Однако DFS найдет цель быстрее. Но если бы кто-то искал члена семьи, который умер очень давно, тогда этот человек был бы ближе к вершине дерева. Тогда BFS обычно будет быстрее, чем DFS. Таким образом, преимущества любого из них зависят от данных и того, что вы ищете.
Еще один пример - Facebook; Предложение о друзьях друзей. Нам нужны непосредственные друзья для предложения, где мы можем использовать BFS. Может быть, найти кратчайший путь или определить цикл (с помощью рекурсии), мы можем использовать DFS.
Поиск в ширину, как правило, является наилучшим подходом, когда глубина дерева может изменяться, и вам нужно только найти часть дерева для решения. Например, поиск кратчайшего пути от начального значения до конечного значения является хорошим местом для использования BFS.
Поиск по глубине обычно используется, когда вам нужно выполнить поиск по всему дереву. Его проще реализовать (с использованием рекурсии), чем BFS, и требует меньшего количества состояний: в то время как BFS требует хранения всей "границы", DFS требует только сохранения списка родительских узлов текущего элемента.
DFS более компактен, чем BFS, но может пойти на ненужную глубину.
Их имена показательны: если есть большая ширина (то есть большой фактор ветвления), но очень ограниченная глубина (например, ограниченное количество "ходов"), то DFS может быть более предпочтительным, чем BFS.
По IDDFS
Следует отметить, что есть менее известный вариант, который объединяет эффективность использования пространства DFS, но (совокупно) посещение BFS в порядке уровней является итеративным углублением поиска в глубину. Этот алгоритм пересматривает некоторые узлы, но он вносит только постоянный коэффициент асимптотической разности.
Когда вы подходите к этому вопросу как к программисту, выделяется один фактор: если вы используете рекурсию, то поиск в глубину проще реализовать, потому что вам не нужно поддерживать дополнительную структуру данных, содержащую узлы, которые еще предстоит исследовать.
Вот поиск в глубину для неориентированного графа, если вы храните "уже посещенную" информацию в узлах:
def dfs(origin): # DFS from origin:
origin.visited = True # Mark the origin as visited
for neighbor in origin.neighbors: # Loop over the neighbors
if not neighbor.visited: dfs(next) # Visit each neighbor if not already visited
При хранении "уже посещенной" информации в отдельной структуре данных:
def dfs(node, visited): # DFS from origin, with already-visited set:
visited.add(node) # Mark the origin as visited
for neighbor in node.neighbors: # Loop over the neighbors
if not neighbor in visited: # If the neighbor hasn't been visited yet,
dfs(node, visited) # then visit the neighbor
dfs(origin, set())
Сравните это с поиском в ширину, где вам нужно поддерживать отдельную структуру данных для списка узлов, которые еще предстоит посетить, несмотря ни на что.
Одним из важных преимуществ BFS будет то, что его можно использовать для поиска кратчайшего пути между любыми двумя узлами в невзвешенном графе. Принимая во внимание, что мы не можем использовать DFS для одного и того же.
Ниже приводится исчерпывающий ответ на ваш вопрос.
Проще говоря:
Алгоритм поиска в ширину (BFS), от его имени "Ширина", обнаруживает всех соседей узла по внешним краям узла, затем он обнаруживает непосещенных соседей ранее упомянутых соседей по их внешним краям и так далее, пока все посещаются узлы, доступные из исходного источника (мы можем продолжить и взять другой исходный источник, если остались непосещенные узлы и т. д.). Вот почему его можно использовать для поиска кратчайшего пути (если он есть) от узла (исходного источника) до другого узла, если веса ребер одинаковы.
Алгоритм поиска в глубину (DFS), от его названия "Глубина", обнаруживает непосещенных соседей последнего обнаруженного узла x через его внешние края. Если нет непосещенного соседа от узла x, алгоритм выполняет обратное отслеживание, чтобы обнаружить непосещенных соседей узла (через его внешние ребра), из которого был обнаружен узел x, и так далее, пока не будут посещены все узлы, доступные из исходного источника. (мы можем продолжить и взять другой исходный источник, если остались непосещенные узлы и так далее).
И BFS, и DFS могут быть неполными. Например, если фактор ветвления узла бесконечен или очень велик для поддержки ресурсов (памяти) (например, при сохранении узлов, которые будут обнаружены следующими), то BFS не завершается, даже если искомый ключ может находиться на расстоянии нескольких граней из исходного источника. Этот бесконечный фактор ветвления может быть из-за бесконечного выбора (соседних узлов) от данного узла для обнаружения. Если глубина бесконечна или очень велика для поддержки ресурсов (памяти) (например, при сохранении узлов, которые будут обнаружены следующими), то DFS не завершается, даже если найденный ключ может быть третьим соседом исходного источника. Эта бесконечная глубина может быть из-за ситуации, когда для каждого узла, обнаруженного алгоритмом, есть по крайней мере новый выбор (соседний узел), который ранее не посещался.
Таким образом, мы можем сделать вывод, когда использовать BFS и DFS. Предположим, мы имеем дело с управляемым ограниченным фактором ветвления и управляемой ограниченной глубиной. Если искомый узел неглубокий, т.е. достижим после некоторых ребер из исходного источника, то лучше использовать BFS. С другой стороны, если искомый узел является глубоким, т.е. достижимым после большого количества ребер от исходного источника, то лучше использовать DFS.
Например, в социальной сети, если мы хотим найти людей, которые имеют схожие интересы с конкретным человеком, мы можем применить BFS от этого человека в качестве исходного источника, потому что в большинстве случаев эти люди будут его прямыми друзьями или друзьями друзей, т.е. или два края далеко. С другой стороны, если мы хотим найти людей, у которых совершенно разные интересы к конкретному человеку, мы можем применить DFS от этого человека в качестве исходного источника, потому что в большинстве случаев эти люди будут очень далеко от него, то есть друг друга друга..... т.е. слишком много ребер далеко.
Приложения BFS и DFS могут различаться также из-за механизма поиска в каждом из них. Например, мы можем использовать либо BFS (при условии, что фактор ветвления управляемый), либо DFS (при условии, что глубина управляема), когда мы просто хотим проверить достижимость от одного узла к другому, не имея информации о том, где этот узел может находиться. Также они оба могут решать одни и те же задачи, например, топологическую сортировку графа (если есть). BFS можно использовать для поиска кратчайшего пути с ребрами единичного веса от узла (исходный источник) к другому. Принимая во внимание, что DFS может использоваться для исчерпания всех вариантов из-за своей природы углубления, например, обнаружения самого длинного пути между двумя узлами в ациклическом графе. Также DFS можно использовать для обнаружения цикла на графике.
В конце концов, если у нас есть бесконечная глубина и бесконечный коэффициент ветвления, мы можем использовать итеративный поиск с углублением (IDS).
Я думаю, это зависит от того, с какими проблемами вы столкнулись.
- кратчайший путь на простом графе -> bfs
- все возможные результаты -> dfs
- поиск по графу (трактуйте дерево, мартикс тоже как граф) -> dfs ....
Для BFS мы можем рассмотреть пример Facebook. Мы получаем предложение добавить друзей из профиля FB из профиля других друзей. Предположим, что A->B, а B->E и B->F, поэтому A получит предложение для E And F. Они должны использовать BFS для чтения до второго уровня. DFS больше основывается на сценариях, в которых мы хотим прогнозировать что-то на основе данных, которые мы имеем от источника до места назначения. Как уже упоминалось о шахматах или судоку. Если у меня все по-другому, я считаю, что DFS следует использовать для кратчайшего пути, потому что DFS сначала будет покрывать весь путь, а затем мы сможем выбрать лучший. Но поскольку BFS будет использовать подход жадности, возможно, это выглядит как кратчайший путь, но конечный результат может отличаться. Дайте мне знать, верно ли мое понимание.
Некоторые алгоритмы зависят от конкретных свойств DFS (или BFS) для работы. Например, алгоритм Хопкрофта и Тарьяна для поиска 2-соединенных компонентов использует тот факт, что каждый уже посещенный узел, с которым столкнулась DFS, находится на пути от корневого до текущего исследуемого узла.
По свойствам DFS и BFS. Например, когда мы хотим найти кратчайший путь. мы обычно используем BFS, это может гарантировать "самый короткий". но только dfs может гарантировать, что мы можем прийти с этой точки, может достичь этой точки, не может гарантировать "самый короткий".
Когда ширина дерева очень велика, а глубина мала, используйте DFS, так как стек рекурсии не будет переполнен. Используйте BFS, когда ширина мала, а глубина очень велика, чтобы пройти по дереву.
Поскольку при глубинном поиске в процессе обработки узлов используется стек, обратное отслеживание обеспечивается DFS. Поскольку при поиске в ширину используется очередь, а не стек, для отслеживания того, какие узлы обрабатываются, обратный отслеживание не обеспечивается BFS.
Это хороший пример, чтобы продемонстрировать, что BFS в некоторых случаях лучше, чем DFS. https://leetcode.com/problems/01-matrix/
При правильном применении оба решения должны посещать ячейки, которые имеют большее расстояние, чем текущая ячейка +1. Но DFS неэффективен и неоднократно посещал одну и ту же ячейку, что приводит к сложности O(n*n).
Например,
1,1,1,1,1,1,1,1,
1,1,1,1,1,1,1,1,
1,1,1,1,1,1,1,1,
0,0,0,0,0,0,0,0,
Это зависит от ситуации, в которой он используется. Когда у нас возникает проблема обхода графа, мы делаем это для какой-то цели. Когда существует проблема поиска кратчайшего пути в невзвешенном графе или обнаружения двудольного графа, мы можем использовать BFS. Для задач обнаружения цикла или любой логики, требующей возврата назад, мы можем использовать DFS.
Этот вопрос несколько устарел, но отличный пример из современной видеоигры "Битва героев". В типичном подземелье босса ваша цель - победить босса, после чего у вас есть возможность либо покинуть это конкретное подземелье, либо продолжить исследовать его на предмет добычи. Но в целом, боссы далеки от вашей точки появления. Игра предлагает автоматическую функцию прохождения подземелья, которая в основном проводит вашего персонажа через подземелье, встречая врагов по ходу дела. Это реализовано с помощью алгоритма поиска в глубину, так как цель состоит в том, чтобы пройти как можно глубже в подземелье, прежде чем возвращаться назад.