Получить уравнение для 3d формы
У меня есть 2 массива, скажем, X и Y. У каждого есть 5 элементов. Теперь для каждой возможной комбинации (X,Y) у меня есть значение Z, поэтому Z - это матрица 5x5.
Я ищу, чтобы найти формулу, например, Z = F (X,Y). Любая идея о том, как это можно сделать.
Я пробовал поверхностную диаграмму MS Excel, но она не дает никакого уравнения или подгонки кривой на поверхностных диаграммах.
2 ответа
В общем, я бы предложил использовать для этой задачи какое-то другое программное обеспечение, например SciLab или Matlab. Эти продукты более математические, чем в Excel. Но в Excel есть некоторые встроенные функции, которые, возможно, помогут вам.
Первое примечание: вам нужно будет использовать надстройку под названием "Солвер". Эта надстройка поставляется вместе с Excel, но, возможно, не установлена по умолчанию в вашей установке. Одно описание (есть тысячи доступных на www), как установить эту надстройку, вы найдете здесь: Надстройка Solver
Если вы закончили с этим, следующим шагом будет создание листа с данными. Я попытался сгенерировать пример, показанный на картинке ниже.
Диапазон C5:G9содержит матрицу, которую вы хотите аппроксимировать функцией. Так что это матрица z=f(x,y).
Диаграмма рядом - это только 3D-график ваших (в данном случае моих) исходных данных.
Теперь это станет немного математическим.... Вам нужен общий тип функции, который будет использоваться для аппроксимации. Качество результата зависит от того, насколько хорошо эта функция может приблизиться к вашим данным. В примере я использовал подход с приближением 2-го порядка (максимальные квадратичные члены). Мой пример функции z=a*x^2 + b*y^2 + c *x*y + d*x + e*y +f, Если вам нужно больше, попробуйте это с термином третьего порядка (включая также x^3, y^3, ...). Я не хотел делать это в примере, потому что я ненавижу печатать длинные формулы в Excel.
Ввод длинной формулы является следующим шагом:
Теперь мы должны заполнить ассортимент C15:G19 со значениями рассчитанной формулы. Но перед этим мы должны определить коэффициенты полинома в диапазоне J14:J19, В качестве начального значения вы можете использовать только 1 для всех коэффициентов (на рисунке показано решение после запуска решателя)
Формула в ячейке C15 имеет вид =$J$14*C$14^2+$J$15*$B15^2+$J$16*C$14*$B15+$J$17*C$14+$J$18*$B15+$J$19Должно быть легко скопировать его в другие ячейки Матрицы.
График рядом с этим показывает результат нашей функции приближения.
Теперь мы должны подготовить решатель. Решатель должен как-то оптимизировать. Поэтому нам нужно определить функцию, которая показывает качество нашего приближения. Я использовал значение наименьшего квадрата... Посмотрите на WWW для объяснений. В диапазоне C24:G28 Я рассчитал квадраты различий от нашей функции приближения к исходным данным. Ячейка С24 имеет формулу =(C15-C5)^2
Теперь мы близки к завершению. Просто скопируйте эту формулу в остальную часть диапазона и затем добавьте одну очень важную ячейку:
Введите сумму диапазона C24:G28 в ячейке H29 Это значение является суммой ошибки или, лучше сказать, разницы нашей функции приближения с исходными точками данных.
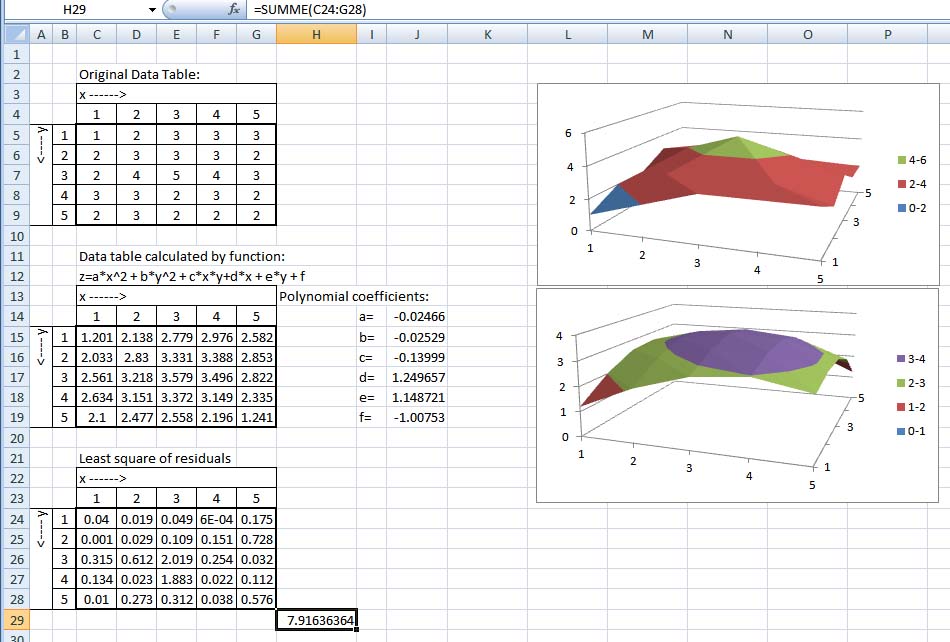
Нове самое главное!!! Выберите Cell H29 и запустите надстройку солвера:
Это окно появится (извините, у меня на компьютере установлена немецкая версия Excel)
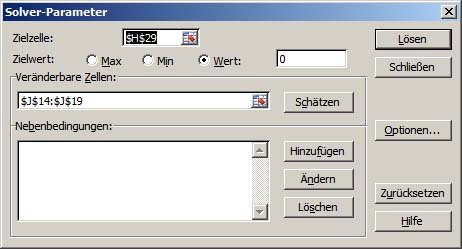
Просто заполните значение для целевой ячейки $H$29, целевое значение =0 и переменные ячейки (важно) $J$14;$J$19
Нажмите "решить" и…. Tada полиномиальные коэффициенты были изменены, чтобы соответствовать вашим данным с функцией.
Это то, что вы искали???
С наилучшими пожеланиями, Аксель
Вы можете зайти в Google и попробовать ThreeDify Excel Grapher v4.5, надстройку для Excel, которая включает в себя установщик трехмерных уравнений с автоматическим поиском уравнений.