Группировка многих точек в ближайшие пары - Python + LP
У меня есть список, который содержит shop_id, широту и долготу. Предполагая, что у нас есть равное количество очков, я хотел бы сопоставить каждый магазин с другим магазином так, чтобы наши связи были уникальными, и мы минимизировали общее расстояние.
Мне было любопытно, если бы мой подход не был слишком глупым и каким был бы лучший. В настоящее время это работает за разумное количество времени (час) за 1000 очков.
Представьте, что у нас есть такой список:
shops = [[1, '53.382072', '-2.7262165'],
[2, '52.478499', '-0.9222608'],
[3, '52.071258', '-1.2722802'],
...]
И что я использую PuLP для создания файла.lp, используя этот рабочий процесс:
prob = LpProblem("Minimise distance",LpMinimize)
# Variables
x = []
xnames = []
for one in store_connect(shops):
xnames.append(one)
x.append(LpVariable(one,0,1,LpInteger))
print("Created %d variables" % len(x))
# Objective
prob += pulp.lpSum([i[1]*x[i[0]] for i in enumerate(distances(shops))])
print("Created objective")
# Constraints
counter = 0
for constraint_rw in all_constraints(shops):
prob += pulp.lpSum(x[xnames.index(one_cn)] for one_cn in constraint_rw) == 1
counter += 1
if counter % 10 == 0:
print("Added %d contraints out of %d" % (counter,len(shops)))
# Save "LP" file for other solvers
prob.writeLP("for_cplex.lp")
Где я вызываю несколько функций генератора (чтобы помочь оперативной памяти...)
def store_connect(shops):
"""
Cross stores and return connection e.g. "v1-2" by ID
"""
for i in range(len(shops)-1):
for j in range(i+1,len(shops)):
yield 'v'+str(shops[i][0])+'-'+str(shops[j][0])
def distances(shops):
"""
Return distance in miles for crosses
"""
for i in range(len(shops)-1):
for j in range(i+1,len(shops)):
yield haversine([shops[i][1],shops[i][2]],
[shops[j][1],shops[j][2]])
def all_constraints(shops):
"""
Return constraint row
"""
for a in shops:
cons = []
for b in shops:
if a[0]<b[0]:
cons.append("v"+str(a[0])+"-"+str(b[0]))
elif a[0]>b[0]:
cons.append("v"+str(b[0])+"-"+str(a[0]))
yield cons
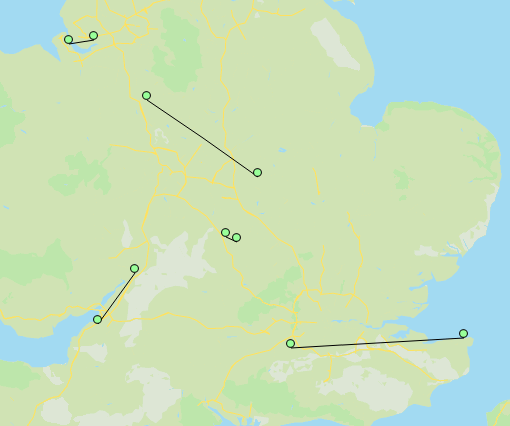
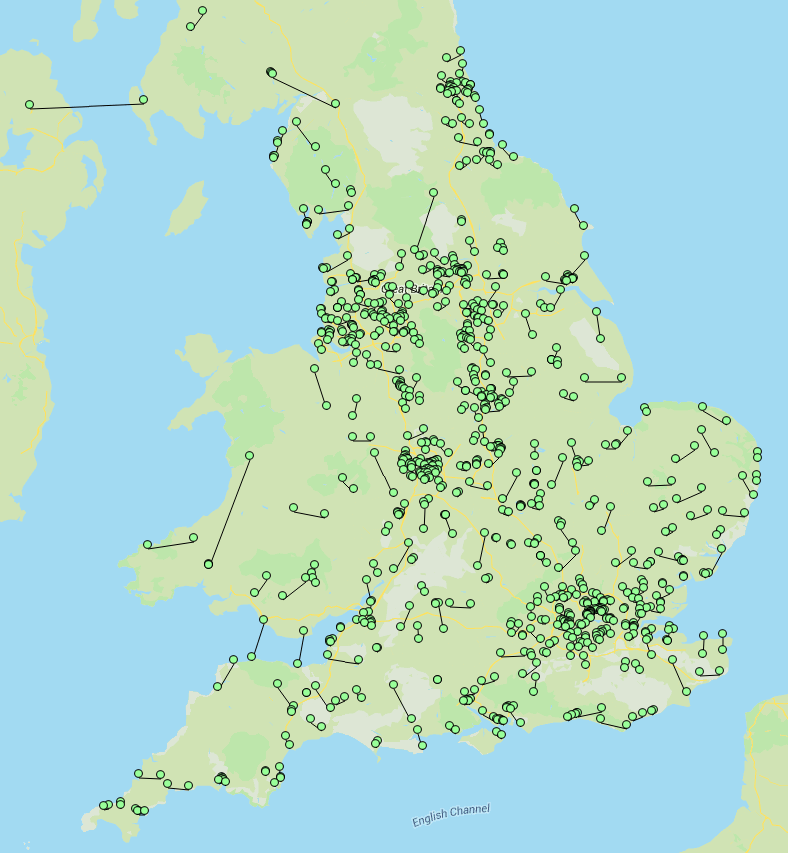
Если я запускаю это в 100 магазинах, это очень быстро, и я могу использовать солвер PuLP по умолчанию. В противном случае я отправляю файл LP в CPLEX на серверах NEOS. Я создал небольшую вспомогательную функцию, которая визуализирует полученные совпадения:
Вот как выглядит мой LP-файл для тривиального примера из 10 магазинов (усеченных):
Minimize
OBJ: 131.513 v1_10 + 97.686 v1_2 + 109.107 v1_3 + 36.603 v1_4 + 11.586 v1_5
+ 109.067 v1_6 + 113.862 v1_7 + 169.371 v1_8 + 220.098 v1_9 + 101.958 v2_10
+ 31.793 v2_3 + 61.792 v2_4 + 105.822 v2_5 + 73.055 v2_6 + 32.008 v2_7
+ 81.627 v2_8 + 122.493 v2_9 + 72.945 v3_10 + 72.983 v3_4 + 114.609 v3_5
+ 46.098 v3_6 + 5.555 v3_7 + 60.305 v3_8 ...
Subject To
_C1: v1_10 + v1_2 + v1_3 + v1_4 + v1_5 + v1_6 + v1_7 + v1_8 + v1_9 = 1
_C10: v1_10 + v2_10 + v3_10 + v4_10 + v5_10 + v6_10 + v7_10 + v8_10 + v9_10
= 1
_C2: v1_2 + v2_10 + v2_3 + v2_4 + v2_5 + v2_6 + v2_7 + v2_8 + v2_9 = 1
_C3: v1_3 + v2_3 + v3_10 + v3_4 + v3_5 + v3_6 + v3_7 + v3_8 + v3_9 = 1
_C4: v1_4 + v2_4 + v3_4 + v4_10 + v4_5 + v4_6 + v4_7 + v4_8 + v4_9 = 1
_C5: v1_5 + v2_5 + v3_5 + v4_5 + v5_10 + v5_6 + v5_7 + v5_8 + v5_9 = 1
...
Binaries
v1_10
v...
End
Результат:
Status: Optimal
Total minimised distance (miles): 190.575
Наконец, вот более крупный пример на 1000 баллов:
1 ответ
Рассмотрим решение pandas (пакет анализа данных Python). Моя элементарная геометрия напоминает мне, что между двумя точками самое близкое расстояние - прямая линия, которая в координатной плоскости - гипотенуза между точками Lat и Lng.
Ниже сначала выполняется декартово произведение между магазинами (все возможные комбинации между наборами), а затем рассчитывается гипотенуза с использованием географических координат. Оттуда минимиум агрегируется:
import pandas as pd
# ORIGINAL LIST
shops = [[1, 53.382072, -2.7262165],
[2, 52.478499, -0.9222608],
[3, 52.071258, -1.2722802]]
# CONVERTING INTO TWO DUPLICATE SHOPS DATA FRAMES
shopsdfA = pd.DataFrame(shops, columns=['ID_A', 'Lat_A', 'Lng_A'])
shopsdfA['key']=1
shopsdfB = pd.DataFrame(shops, columns=['ID_B', 'Lat_B', 'Lng_B'])
shopsdfB['key']=1
# CROSS JOINING BOTH DATA FRAMES FOR CARTESIAN PRODUCT SET
compareshops = pd.merge(shopsdfA, shopsdfB, on='key')[['ID_A', 'Lat_A', 'Lng_A',
'ID_B','Lat_B', 'Lng_B']]
# (REMOVING SHOPS COMPARED TO ITSELF)
compareshops = compareshops[compareshops['ID_A'] != compareshops['ID_B']].\
reset_index(drop=True)
# ID_A Lat_A Lng_A ID_B Lat_B Lng_B
#0 1 53.382072 -2.726217 2 52.478499 -0.922261
#1 1 53.382072 -2.726217 3 52.071258 -1.272280
#2 2 52.478499 -0.922261 1 53.382072 -2.726217
#3 2 52.478499 -0.922261 3 52.071258 -1.272280
#4 3 52.071258 -1.272280 1 53.382072 -2.726217
#5 3 52.071258 -1.272280 2 52.478499 -0.922261
# CALCULATE HYPOTENUSE
compareshops['hypotenuse'] = ((compareshops['Lat_A'] - compareshops['Lat_B']) ** 2 +
(compareshops['Lng_A'] - compareshops['Lng_B']) ** 2) ** (1/2)
# ID_A Lat_A Lng_A ID_B Lat_B Lng_B hypotenuse
#0 1 53.382072 -2.726217 2 52.478499 -0.922261 2.017598
#1 1 53.382072 -2.726217 3 52.071258 -1.272280 1.957591
#2 2 52.478499 -0.922261 1 53.382072 -2.726217 2.017598
#3 2 52.478499 -0.922261 3 52.071258 -1.272280 0.536991
#4 3 52.071258 -1.272280 1 53.382072 -2.726217 1.957591
#5 3 52.071258 -1.272280 2 52.478499 -0.922261 0.536991
# AGGREGATE FOR MINIMUM HYPOTENUSE AND MERGE CORRESPONDING PAIRED IDS
compareshops = pd.merge(compareshops[['ID_A','hypotenuse']].groupby(['ID_A']).min().reset_index(),
compareshops[['ID_B','hypotenuse']], on='hypotenuse')
# (REMOVING SAME STORE PAIRINGS)
compareshops = compareshops[compareshops['ID_A'] != compareshops['ID_B']].\
reset_index(drop=True)[['ID_A','ID_B','hypotenuse']]
# ID_A ID_B hypotenuse
#0 1 3 1.957591
#1 2 3 0.536991
#2 3 2 0.536991
Одной из предполагаемых проблем является то, что ваша карта не имеет перекрывающихся соединений, только одно соединение с каждым магазином. Возможно, потребуется выполнить итеративный расчет гипотенузы, чтобы найти "следующее" кратчайшее расстояние.