Фильтр KALMAN не реагирует на изменения
Я впервые применяю фильтр Калмана для получения значений напряжения от источника. Он работает и стабилизируется при значении напряжения источника, но если затем источник изменяет напряжение, фильтр не адаптируется к новому значению.
Я использую 3 шага:
Получить усиление Калмана
KG = previous_error_in_estimate / ( previous_error_in_estimate + Error_in_measurement )Получить текущую оценку
Estimation = previous_estimation + KG*[measurement - previous_estimation]Рассчитать ошибку в оценке
Error_in_estimate = [1-KG]*previous_error_in_estimate
Дело в том, что при 0 <= KG <= 1 Error_in_estimate уменьшается все больше и больше, и это заставляет KG также уменьшаться все больше и больше (error_in_measurement является постоянной величиной), поэтому в конце оценка зависит только от предыдущей оценки, а текущее измерение не учитывается.
Это предотвращает адаптацию фильтра к изменениям измерения.
Как я могу это сделать?
Спасибо
РЕДАКТИРОВАТЬ:
Отвечая Класу:
Я не уверен, что фильтр Калмана подходит для моей проблемы, так как у меня нет модели системы, у меня просто куча показаний с довольно шумного датчика, измеряющего не очень предсказуемую переменную.
Для простоты представьте, что вы читаете потенциометр (переменный резистор), измененный пользователем, вы не можете предсказать или смоделировать поведение пользователя.
Я реализовал очень простой алгоритм SMA ( Simple Moving Average), и мне было интересно, есть ли лучший способ сделать это.
Является ли фильтр Калмана действительным для такой проблемы?
Если нет, что бы вы предложили?
2-е РЕДАКТИРОВАНИЕ
Спасибо Claes за такую полезную информацию
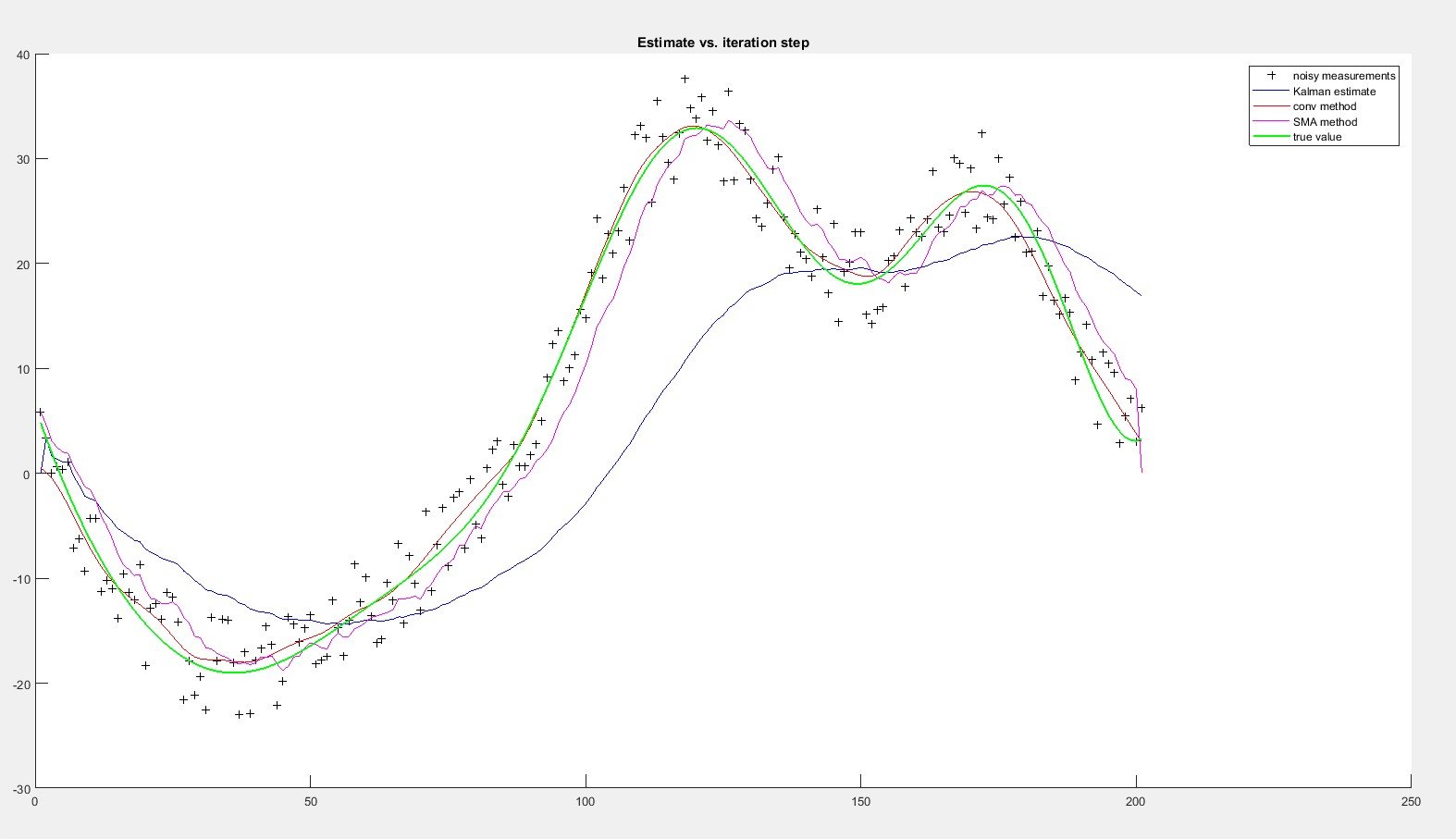
Я проводил некоторые числовые тесты в MathLab (без реальных данных), и свертка с гауссовым фильтром, похоже, дает наиболее точный результат.
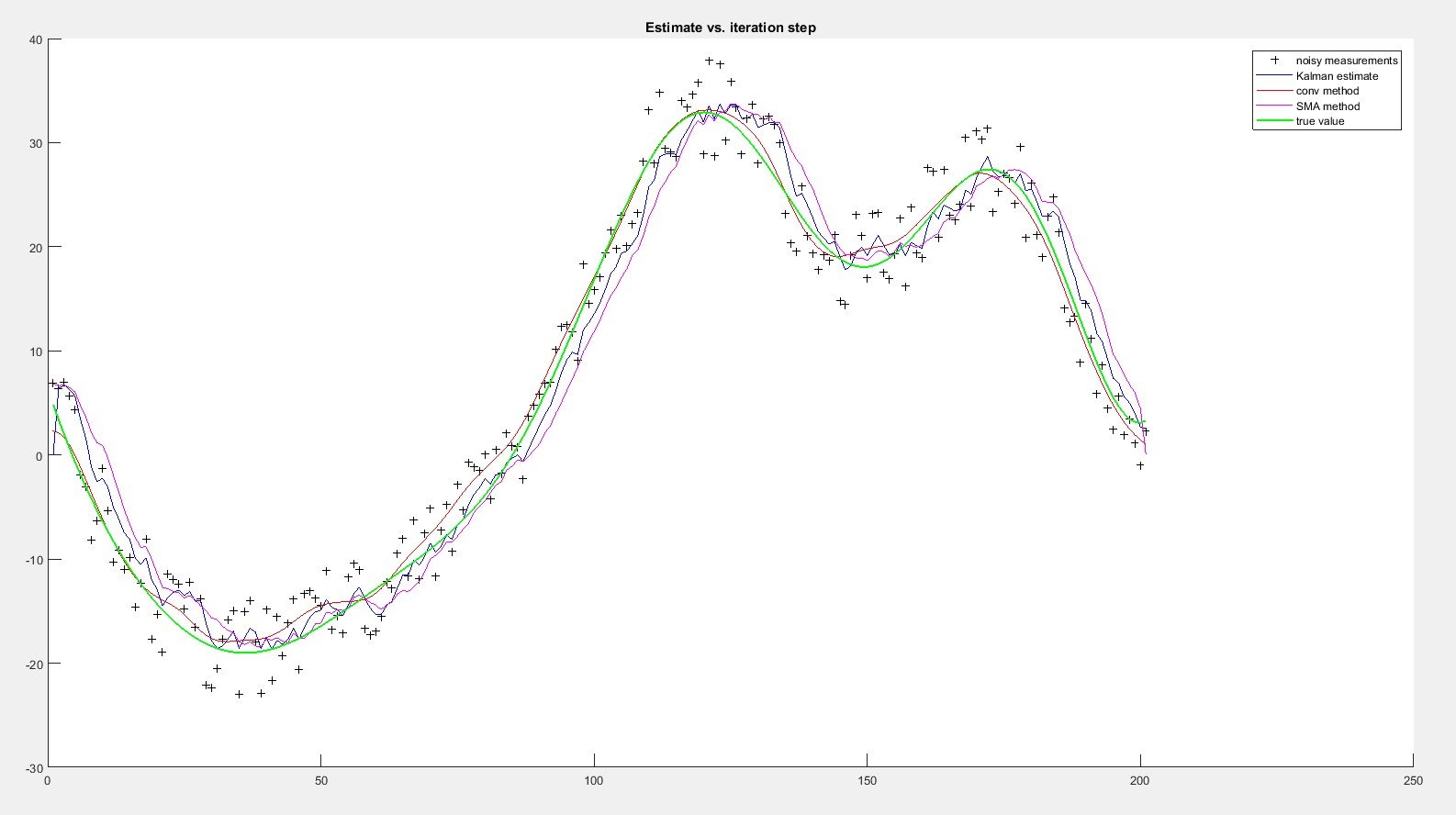
С фильтром Калмана я не знаю, как оценить отклонения процесса и измерения, есть ли способ для этого? Только когда я значительно уменьшу дисперсию измерения, фильтр Калмана, кажется, адаптируется. На предыдущем изображении дисперсия измерения была R=0,1^2 (та, что в исходном примере). Это тот же тест с R=0,01^2
Конечно, это тесты MathLab без реальных данных. Завтра я постараюсь реализовать эти фильтры в реальной системе с реальными данными и посмотреть, смогу ли я получить аналогичные результаты
1 ответ
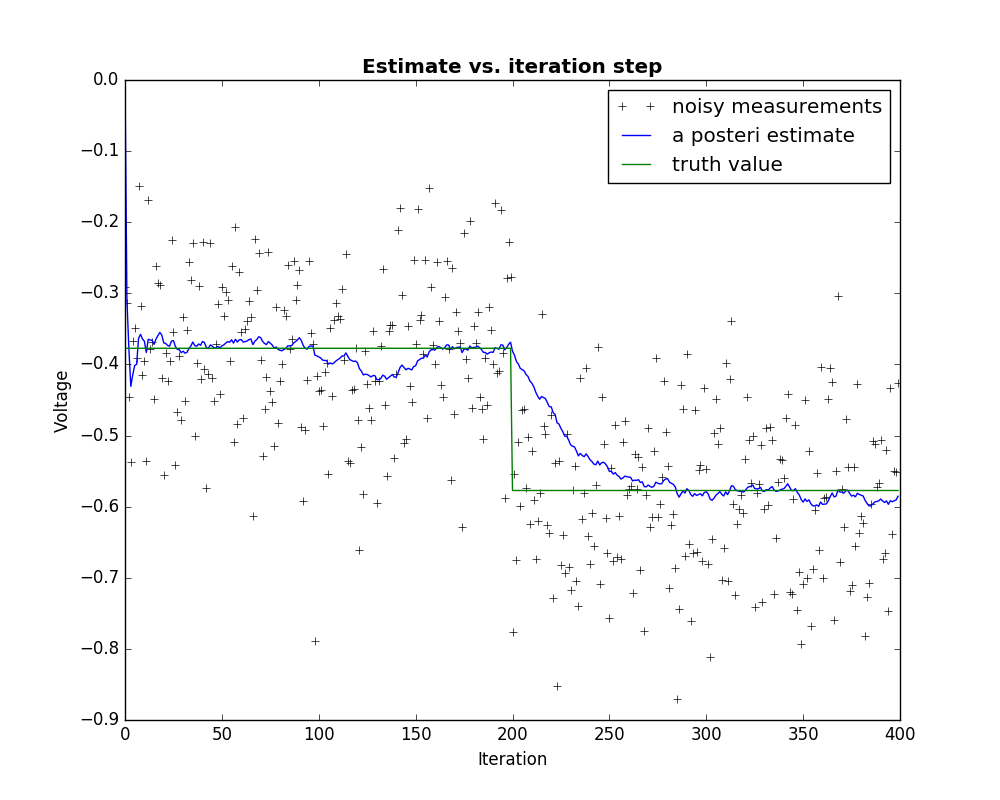
Для вашего примера, вероятно, достаточно простого фильтра МА. Если вы хотите использовать фильтр Калмана, есть отличный пример в кулинарной книге SciPy.
Я изменил код, включив в него изменение шага, чтобы вы могли видеть схождение.
# Kalman filter example demo in Python
# A Python implementation of the example given in pages 11-15 of "An
# Introduction to the Kalman Filter" by Greg Welch and Gary Bishop,
# University of North Carolina at Chapel Hill, Department of Computer
# Science, TR 95-041,
# http://www.cs.unc.edu/~welch/kalman/kalmanIntro.html
# by Andrew D. Straw
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['figure.figsize'] = (10, 8)
# intial parameters
n_iter = 400
sz = (n_iter,) # size of array
x1 = -0.37727*np.ones(n_iter/2) # truth value 1
x2 = -0.57727*np.ones(n_iter/2) # truth value 2
x = np.concatenate((x1,x2),axis=0)
z = x+np.random.normal(0,0.1,size=sz) # observations (normal about x, sigma=0.1)
Q = 1e-5 # process variance
# allocate space for arrays
xhat=np.zeros(sz) # a posteri estimate of x
P=np.zeros(sz) # a posteri error estimate
xhatminus=np.zeros(sz) # a priori estimate of x
Pminus=np.zeros(sz) # a priori error estimate
K=np.zeros(sz) # gain or blending factor
R = 0.1**2 # estimate of measurement variance, change to see effect
# intial guesses
xhat[0] = 0.0
P[0] = 1.0
for k in range(1,n_iter):
# time update
xhatminus[k] = xhat[k-1]
Pminus[k] = P[k-1]+Q
# measurement update
K[k] = Pminus[k]/( Pminus[k]+R )
xhat[k] = xhatminus[k]+K[k]*(z[k]-xhatminus[k])
P[k] = (1-K[k])*Pminus[k]
plt.figure()
plt.plot(z,'k+',label='noisy measurements')
plt.plot(xhat,'b-',label='a posteri estimate')
plt.plot(x,color='g',label='truth value')
plt.legend()
plt.title('Estimate vs. iteration step', fontweight='bold')
plt.xlabel('Iteration')
plt.ylabel('Voltage')