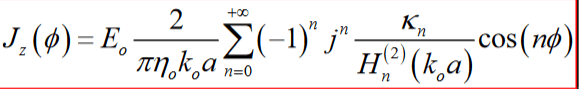Функция построения графиков с суммированием дает неверный результат

Question

У меня есть уравнение, которое должно быть построено, и график выходит неправильно.

Уравнение выглядит следующим образом:

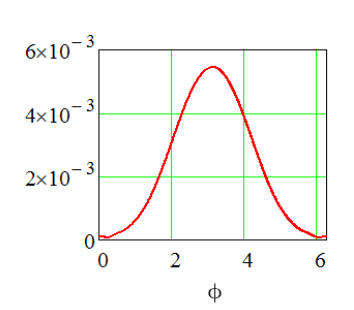
И сюжет должен выглядеть так:

Но мой код:

clear; clc; close all;

eta      = 376.7303134617706554679; % 120pi
ka       = 4;
N        = 24;
coeff    = (2)/(pi*eta*ka);
Jz       = 0;

theta = [0;0.0351015938948580;0.0702031877897160;0.105304781684574;0.140406375579432;0.175507969474290;0.210609563369148;0.245711157264006;0.280812751158864;0.315914345053722;0.351015938948580;0.386117532843438;0.421219126738296;0.456320720633154;0.491422314528012;0.526523908422870;0.561625502317728;0.596727096212586;0.631828690107444;0.666930284002302;0.702031877897160;0.737133471792019;0.772235065686877;0.807336659581734;0.842438253476592;0.877539847371451;0.912641441266309;0.947743035161167;0.982844629056025;1.01794622295088;1.05304781684574;1.08814941074060;1.12325100463546;1.15835259853031;1.19345419242517;1.22855578632003;1.26365738021489;1.29875897410975;1.33386056800460;1.36896216189946;1.40406375579432;1.43916534968918;1.47426694358404;1.50936853747890;1.54447013137375;1.57957172526861;1.61467331916347;1.64977491305833;1.68487650695319;1.71997810084804;1.75507969474290;1.79018128863776;1.82528288253262;1.86038447642748;1.89548607032233;1.93058766421719;1.96568925811205;2.00079085200691;2.03589244590177;2.07099403979662;2.10609563369148;2.14119722758634;2.17629882148120;2.21140041537606;2.24650200927091;2.28160360316577;2.31670519706063;2.35180679095549;2.38690838485035;2.42200997874520;2.45711157264006;2.49221316653492;2.52731476042978;2.56241635432464;2.59751794821949;2.63261954211435;2.66772113600921;2.70282272990407;2.73792432379893;2.77302591769378;2.80812751158864;2.84322910548350;2.87833069937836;2.91343229327322;2.94853388716807;2.98363548106293;3.01873707495779;3.05383866885265;3.08894026274751;3.12404185664236;-3.12404185664236;-3.08894026274751;-3.05383866885265;-3.01873707495779;-2.98363548106293;-2.94853388716807;-2.91343229327322;-2.87833069937836;-2.84322910548350;-2.80812751158864;-2.77302591769378;-2.73792432379893;-2.70282272990407;-2.66772113600921;-2.63261954211435;-2.59751794821949;-2.56241635432464;-2.52731476042978;-2.49221316653492;-2.45711157264006;-2.42200997874520;-2.38690838485035;-2.35180679095549;-2.31670519706063;-2.28160360316577;-2.24650200927091;-2.21140041537605;-2.17629882148120;-2.14119722758634;-2.10609563369148;-2.07099403979662;-2.03589244590177;-2.00079085200691;-1.96568925811205;-1.93058766421719;-1.89548607032233;-1.86038447642748;-1.82528288253262;-1.79018128863776;-1.75507969474290;-1.71997810084804;-1.68487650695319;-1.64977491305833;-1.61467331916347;-1.57957172526861;-1.54447013137375;-1.50936853747890;-1.47426694358404;-1.43916534968918;-1.40406375579432;-1.36896216189946;-1.33386056800461;-1.29875897410975;-1.26365738021489;-1.22855578632003;-1.19345419242517;-1.15835259853032;-1.12325100463546;-1.08814941074060;-1.05304781684574;-1.01794622295088;-0.982844629056025;-0.947743035161167;-0.912641441266309;-0.877539847371451;-0.842438253476592;-0.807336659581735;-0.772235065686877;-0.737133471792019;-0.702031877897161;-0.666930284002303;-0.631828690107445;-0.596727096212586;-0.561625502317728;-0.526523908422871;-0.491422314528013;-0.456320720633154;-0.421219126738296;-0.386117532843439;-0.351015938948581;-0.315914345053722;-0.280812751158864;-0.245711157264007;-0.210609563369149;-0.175507969474290;-0.140406375579432;-0.105304781684575;-0.0702031877897167;-0.0351015938948580;-2.44929359829471e-16];

for n = 0:N
    if n == 0
        kappa  = 1;
    else
        kappa  = 2;
    end

    num    = (-1.^(n)).*(1i.^(n)).*(cos(n.*theta)).*(kappa);
    Hankel = besselh(n,2,ka);
    Jz     = Jz + ((num./Hankel));
end

Jz = Jz.*coeff;
x = linspace(0,2*pi,length(theta));
plot(x,abs(Jz));

Создает следующий неверный сюжет: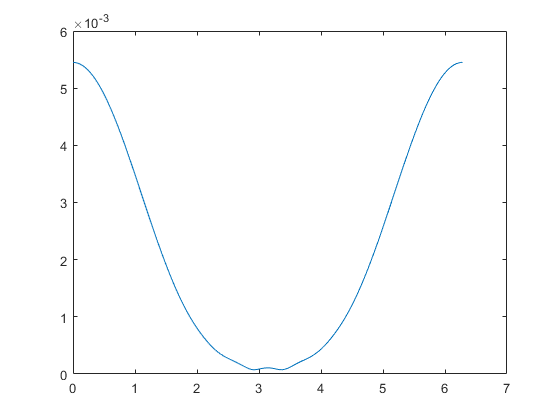

Обратите внимание, что значения тета являются дискретными углами вокруг круглого цилиндра. Уравнение является аналитическим решением для плотности тока для поляризованного цилиндра TMz в 2D.

Answer 1

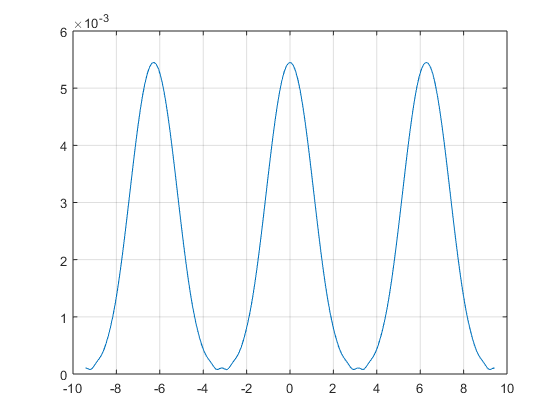
Я думаю, что ваш результат на самом деле правильный, и это простая проблема с графикой или с тем, как вы указываете theta, Поскольку это периодическая функция, давайте нарисуем еще несколько периодов:

function q52693512

eta      = 376.7303134617706554679; % 120pi
ka       = 4;
N        = 24;
coeff    = (2)/(pi*eta*ka);
Jz       = 0;

theta = linspace(-3*pi, 3*pi, 180);
for n = 0:N
    kappa  = 1 + (n>0);
    num    = (-1.^(n)).*(1i.^(n)).*(cos(n.*theta)).*(kappa);
    Hankel = besselh(n,2,ka);
    Jz     = Jz + ((num./Hankel));
end

Jz = Jz.*coeff;
figure(); plot(theta, abs(Jz));

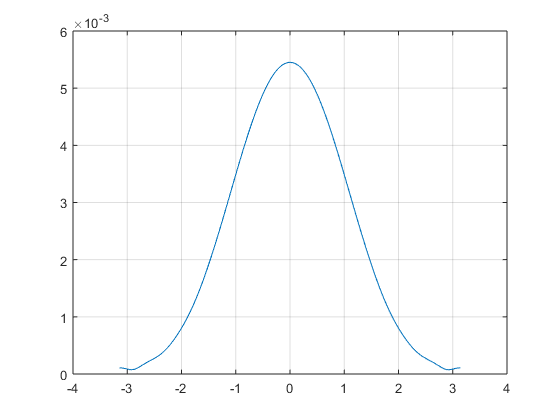
Возможно, вы уже можете видеть, что желаемые результаты уже есть, но смещены на половину периода относительно нашего результата. Это будет понятнее, если мы снова посмотрим на центр (это именно та форма, которую вы хотите, если игнорировать значения горизонтальной оси).

Попробуйте найти какое-то обоснование для ϕ, равного theta ± π/2 (или что-то подобное).