Какова структура непрямого фильтра Калмана (состояние ошибки) и как выводятся уравнения ошибок?

Question

Я пытался внедрить навигационную систему для робота, которая использует инерциальный измерительный блок (IMU) и наблюдения с помощью камер с помощью известных ориентиров, чтобы локализовать себя в своей среде. Для этого я выбрал фильтр Калмана с непрямой обратной связью (Фильтр состояния Калмана с ошибками, ESKF). У меня также был некоторый успех с Extended KF.

Я прочитал много текстов, и два из них, которые я использую для реализации ESKF, - это " Quaternion kinematics для состояния ошибки KF" и "Алгоритм на основе фильтров Калмана для калибровки IMU-камеры" (бумага с платными стенами, google-able), Я использую первый текст, потому что он лучше описывает структуру ESKF, а второй, потому что он содержит детали о модели измерения зрения. В моем вопросе я буду использовать терминологию из первого текста: "номинальное состояние", "состояние ошибки" и "истинное состояние"; которые ссылаются на интегратор IMU, фильтр Калмана, и их состав (номинальные минус ошибки).

На диаграмме ниже показана структура моего ESKF, реализованного в Matlab / Simulink; если вы не знакомы с Simulink, я кратко объясню диаграмму. Зеленая секция - это интегратор номинального состояния, синяя секция - ESKF, а красная секция - сумма номинального и ошибочного состояний. Блоки "RT" - это "Переходы скорости", которые можно игнорировать.

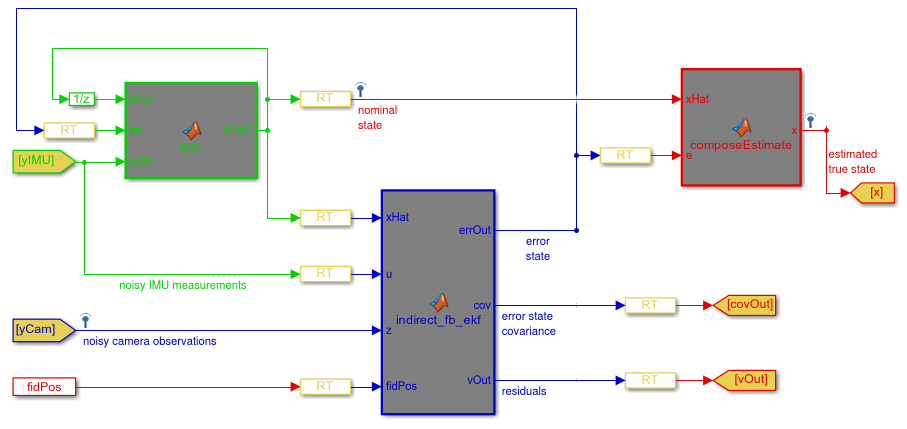
Мой первый вопрос: правильна ли эта структура?

Мой второй вопрос: как выводятся уравнения состояния ошибки для моделей измерения? В моем случае я попытался использовать модель измерения второго текста, но это не сработало.

С уважением,

Answer 1

Ваша блок-схема сочетает в себе два косвенных метода для передачи данных IMU в KF:

1. У вас есть внешний интегратор IMU (зеленый, помеченный "INS", иногда называемый механизацией и описанный вами как "номинальное состояние", но я также видел его под названием "эталонное состояние"). Этот метод свободно интегрирует IMU извне с KF и обычно выбирается таким образом, чтобы вы могли выполнять эту интеграцию с другой (гораздо более высокой) скоростью, чем этап прогнозирования / обновления KF (косвенная форма). Исторически я думаю, что это было популярно, потому что KF, как правило, вычислительно дорогая часть.
2. Вы также подали свой IMU в блок KF как uЯ предполагаю, что это "командный" вход в KF. Это альтернатива внешнему интегратору. В прямом KF вы рассматриваете свои данные IMU как измерения. Для этого ИДУ должно моделировать (положение, скорость и) ускорение и (ориентацию и) угловую скорость: в противном случае это невозможно H такой, что Hx может произвести расчетные выходные условия ИДУ). Если вместо этого вы вводите свои измерения IMU в качестве команды, ваш шаг прогнозирования может просто выступать в качестве интегратора, поэтому вам нужно только моделировать, насколько скорость и ориентация.

Вы должны выбрать только один из этих вариантов. Я думаю, что второй легче понять, но он ближе к прямому фильтру Калмана и требует от вас прогнозирования / обновления для каждой выборки IMU, а не при (я предполагаю) более низкой частоте кадров камеры.

Что касается уравнений измерения для версии (1), в любом KF вы можете предсказать только то, что вы можете узнать из своего состояния. Состояние KF в этом случае является вектором ошибок, и, таким образом, вы можете только предсказать такие вещи, как "ошибка положения". В результате вы должны предварительно подготовить свои измерения в z быть ошибки позиции. Так что сделайте ваши измерения разницей между вашим "предполагаемым истинным состоянием" и вашим положением от "шумных наблюдений с камеры". Эта точная идея может быть представлена xHat вход в косвенный кф. Я ничего не знаю о том, что там происходит с MATLAB/Simulink.

Относительно реальных соображений для блока суммирования (красным) я отсылаю вас к другому ответу о косвенных фильтрах Калмана.

Answer 2

Q1) Ваша модель SIMULINK выглядит подходящей. Позвольте мне пролить некоторый свет на кватернионную механизацию KF, над которой я работал для навигационных приложений.

Поскольку Kalman Filter - это элегантный математический метод, который заимствован из науки о стохастике и измерениях, он может помочь вам уменьшить шум в системе без необходимости тщательного моделирования шума.

Все системы KF начинаются с некоторого предварительного понимания модели, которую вы хотите создать без шума. Измерения возвращаются для лучшего развития состояний (уравнение измерения Y = CX). В вашем случае состояния, о которых вы говорите, являются ошибками в четвертях: 4 значения: dq1, dq2, dq3, dq4.

KF, хорошо работающий в вашем приложении, будет точно определять ориентацию / ориентацию устройства, контролируя погрешность вокруг кватерниона. Кватернионы - это пространственная ориентация любого тела, понимаемая с использованием скаляра и вектора, более конкретно угла и оси.

Уравнения ошибок, о которых вы говорите, являются ковариациями, которые способствуют усилению Калмана. Ковариации обозначают разброс вокруг среднего, и они полезны для понимания того, как центральное / среднее поведение системы меняется со временем. Низкие ковариации означают меньшее отклонение от среднего поведения для любой системы. По мере выполнения циклов KF ковариации продолжают уменьшаться.

Коэффициент Калмана, наконец, используется для компенсации погрешности между оценками измерений и фактическими измерениями, поступающими с камеры.

Опять же, этот элегантный метод сначала гарантирует, что ошибки в значениях кватернионов сходятся около нуля.

Q2) EKF - отличный метод для использования, если у вас есть метод построения нелинейных измерений. Будьте очень осторожны при использовании EKF, если в вашей системе слишком много преобразований, то есть не пытайтесь реконструировать измерения, используя преобразования ваших состояний, это серьезно влияет на корректность модели, и поскольку ковариации шума не будут подвергаться аналогичным преобразованиям, возникнет вероятность достижения сингулярности, как только матрицы не обратимы.

Вы могли бы взглянуть на схемы KF с постоянным усилением, которые избавили бы вас от распространения ковариации и сэкономили бы значительные вычислительные усилия и время. Эти методы довольно новые и выглядят очень многообещающе. Они активно поглощают P(ковариацию ошибок), Q(ковариацию шума модели) и R(ковариацию шума измерения) и хорошо работают со схемами EKF.