Описание тега cdf
CDF is an acronym for cumulative distribution function. While the pdf gives the probability density of each value of a random variable, the cdf (often denoted F(x)) gives the probability that the random variable will be less than or equal to a specified value.
A cumulative density function describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x.
The cdf of a discrete random variable is the summation of the probability mass function (pmf) of that distribution. If the random variable is continuous, this turns out to be the integral of the probability density function (pdf).
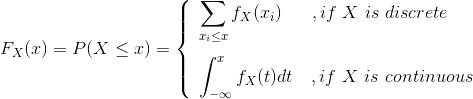
In applied statistics, cdfs are important in comparing distributions, playing a role in plots (e.g., pp-plots), and hypothesis tests (e.g., the Kolmogorov-Smirnov test).
Strongly related to probability-density