Равномерная выборка случайно из n-мерного единичного симплекса

Question

Равномерная выборка случайным образом из n-мерного симплекса - это причудливый способ сказать, что вы хотите n случайных чисел, таких, чтобы

• все они неотрицательны,
• они складываются в один, и
• каждый возможный вектор из n неотрицательных чисел, суммирующих одно, одинаково вероятен.

В случае n=2 вы хотите сделать выборку равномерно из сегмента линии x+y=1 (т.е. y=1-x), который находится в положительном квадранте. В случае n=3 вы производите выборку из треугольной части плоскости x+y+z=1, которая находится в положительном октанте R3:

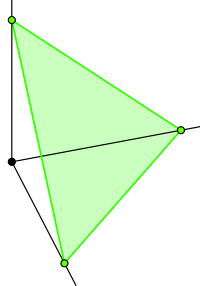
(Изображение с http://en.wikipedia.org/wiki/Simplex.)

Обратите внимание, что выборка n равномерных случайных чисел, а затем их нормализация, чтобы они суммировались в одно, не работает. Вы в конечном итоге смещены в сторону менее экстремальных чисел.

Точно так же, выбор n-1 равномерных случайных чисел и затем принятие n-го равным одному минус сумма их также вводит смещение.

Википедия предлагает два алгоритма, чтобы сделать это правильно: http://en.wikipedia.org/wiki/Simplex(Хотя второй в настоящее время утверждает, что он верен только на практике, а не в теории. Я надеюсь это исправить или проясните это, когда я пойму это лучше. Сначала я застрял в "ПРЕДУПРЕЖДЕНИИ: такая-то и такая-то статья утверждает, что следующее неверно" на этой странице Википедии, и кто-то другой превратил это в предупреждение "работает только на практике".)

Наконец, вопрос: что вы считаете лучшей реализацией симплексной выборки в Mathematica (желательно с эмпирическим подтверждением того, что это правильно)?

Смежные вопросы

• Генерация вероятностного распределения
• java случайные проценты

Answer 1

Этот код может работать:

samples[n_] := Differences[Join[{0}, Sort[RandomReal[Range[0, 1], n - 1]], {1}]]

В основном вы просто выбираете n - 1 места на интервале [0,1] разделить его, а затем взять размер каждой из частей, используя Differences,

Быстрый пробег Timing на этом видно, что это немного быстрее, чем первый ответ Януса.

Answer 2

Немного покопавшись, я нашел эту страницу, которая дает отличную реализацию Dirichlet Distribution. Оттуда кажется, что было бы довольно просто следовать методу Википедии 1. Это кажется лучшим способом сделать это.

В качестве теста:

In[14]:= RandomReal[DirichletDistribution[{1,1}],WorkingPrecision->25]
Out[14]= {0.8428995243540368880268079,0.1571004756459631119731921}
In[15]:= Total[%]
Out[15]= 1.000000000000000000000000

Сюжет из 100 образцов:

http://www.public.iastate.edu/~zdavkeos/simplex-sample.png

Answer 3

Я с zdav: кажется, что дистрибутив Dirichlet - самый простой путь, и алгоритм выборки дистрибутива Dirichlet, на который ссылается zdav, также представлен на странице Википедии в дистрибутиве Dirichlet.

Внедрение полной реализации дистрибутива Dirichlet требует больших усилий, так как все, что вам действительно нужно, это n случайный Gamma[1,1] образцы. Сравните ниже
Простая реализация

SimplexSample[n_, opts:OptionsPattern[RandomReal]] :=
  (#/Total[#])& @ RandomReal[GammaDistribution[1,1],n,opts]

Полная реализация Дирихле

DirichletDistribution/:Random`DistributionVector[
 DirichletDistribution[alpha_?(VectorQ[#,Positive]&)],n_Integer,prec_?Positive]:=
    Block[{gammas}, gammas = 
        Map[RandomReal[GammaDistribution[#,1],n,WorkingPrecision->prec]&,alpha];
      Transpose[gammas]/Total[gammas]]

SimplexSample2[n_, opts:OptionsPattern[RandomReal]] := 
  (#/Total[#])& @ RandomReal[DirichletDistribution[ConstantArray[1,{n}]],opts]

тайминг

Timing[Table[SimplexSample[10,WorkingPrecision-> 20],{10000}];]
Timing[Table[SimplexSample2[10,WorkingPrecision-> 20],{10000}];]
Out[159]= {1.30249,Null}
Out[160]= {3.52216,Null}

Таким образом, полный Дирихле в 3 раза медленнее. Если вам нужно m>1 выборочных точек за раз, вы можете выиграть, выполнив (#/Total[#]&)/@RandomReal[GammaDistribution[1,1],{m,n}],

Answer 4

Вот хорошая краткая реализация второго алгоритма из Википедии:

SimplexSample[n_] := Rest@# - Most@# &[Sort@Join[{0,1}, RandomReal[{0,1}, n-1]]]

Это адаптировано отсюда: http://www.mofeel.net/1164-comp-soft-sys-math-mathematica/14968.aspx(Первоначально он имел Союз вместо Sort@Join - последний немного быстрее.)

(Смотрите комментарии для некоторых доказательств того, что это правильно!)

Answer 5

Я создал алгоритм равномерной генерации случайных чисел по симплексу. Подробности можно найти в следующей ссылке: http://www.tandfonline.com/doi/abs/10.1080/03610918.2010.551012

Вкратце, вы можете использовать следующие формулы рекурсии, чтобы найти случайные точки над n-мерным симплексом:

x₁= 1-R₁^{1 / n-1}

x_k= (1-Σ_{i = 1}^kx_i) (1-R_k^{1 / nk}), k = 2,..., n-1

x_n= 1-Σ_{i = 1}^n-1x_i

Где R_i - это случайные числа от 0 до 1.

Сейчас я пытаюсь создать алгоритм для генерации случайных равномерных выборок из ограниченного симплекса. Это пересечение между симплексом и выпуклым телом.

Answer 6

Старый вопрос, и я опаздываю на вечеринку, но этот метод намного быстрее, чем принятый ответ, если он реализован эффективно.

В коде системы Mathematica:# / Total[#,{2}]&@ [email protected] [{0,1},{n,d}]

Говоря простым языком, вы генерируете n строк * d столбцов случайных чисел, равномерно распределенных между 0 и 1. Затем возьмите Журнал всего. Затем нормализуйте каждую строку, разделив каждый элемент в строке на общее количество строк. Теперь у вас есть n образцов, равномерно распределенных по симплексу (d-1).

Если вы нашли этот метод здесь: https://mathematica.stackexchange.com/questions/33652/uniformly-distributed-n-dimensional-probability-vectors-over-a-simplex

Признаюсь, я не уверен, почему это работает, но он проходит все статистические тесты, которые я могу придумать. Если у кого-то есть доказательство того, почему этот метод работает, я бы с удовольствием его увидел!