Что такое "энтропия и получение информации"?
Я читаю эту книгу ( NLTK), и это сбивает с толку. Энтропия определяется как:
Энтропия - это сумма вероятностей каждой метки, умноженная на логарифмическую вероятность той же самой метки.
Как я могу применить энтропию и максимальную энтропию с точки зрения интеллектуального анализа текста? Может ли кто-нибудь дать мне простой, простой пример (визуальный)?
7 ответов
Я предполагаю, что энтропия упоминалась в контексте построения деревьев решений.
Чтобы проиллюстрировать это, представьте себе задачу научиться классифицировать имена по группам мужчин и женщин. Это дается список имен, каждый из которых помечены либо m или же f Мы хотим изучить модель, которая соответствует данным и может использоваться для прогнозирования пола нового невидимого имени.
name gender
----------------- Now we want to predict
Ashley f the gender of "Amro" (my name)
Brian m
Caroline f
David m
Первым шагом является определение того, какие особенности данных относятся к целевому классу, который мы хотим предсказать. Некоторые примеры функций включают в себя: первую / последнюю букву, длину, количество гласных, заканчивается ли это гласной и т. Д. Итак, после извлечения признаков наши данные выглядят так:
# name ends-vowel num-vowels length gender
# ------------------------------------------------
Ashley 1 3 6 f
Brian 0 2 5 m
Caroline 1 4 8 f
David 0 2 5 m
Цель состоит в том, чтобы построить дерево решений. Примером дерева будет:
length<7
| num-vowels<3: male
| num-vowels>=3
| | ends-vowel=1: female
| | ends-vowel=0: male
length>=7
| length=5: male
в основном каждый узел представляет тест, выполненный для одного атрибута, и мы идем влево или вправо в зависимости от результата теста. Мы продолжаем обходить дерево, пока не достигнем конечного узла, который содержит прогноз класса (m или же f)
Поэтому, если мы запустим имя Amro по этому дереву, мы начнем с проверки " есть длина <7? " И ответ " да", поэтому мы идем по этой ветви. После ветки следующий тест " количество гласных <3? " Снова оценивается как true. Это приводит к листовому узлу с надписью m и, таким образом, предсказание является мужским (что мне и случается, поэтому дерево предсказало результат правильно).
Дерево решений построено в нисходящем порядке, но вопрос в том, как выбрать, какой атрибут разделить на каждом узле? Ответ заключается в том, чтобы найти функцию, которая наилучшим образом разбивает целевой класс на самые чистые из возможных дочерних узлов (то есть: узлы, которые не содержат смесь как мужского, так и женского, а скорее чистые узлы только с одним классом).
Эта мера чистоты называется информацией. Он представляет ожидаемый объем информации, который понадобится для указания того, должен ли новый экземпляр (имя) быть классифицирован как мужской или женский, учитывая пример, который достиг узла. Мы рассчитываем это на основе количества мужских и женских классов в узле.
С другой стороны, энтропия - это мера нечистоты (противоположность). Определяется для двоичного класса со значениями a / b как:
Entropy = - p(a)*log(p(a)) - p(b)*log(p(b))
Эта двоичная энтропийная функция изображена на рисунке ниже (случайная величина может принимать одно из двух значений). Он достигает своего максимума, когда вероятность p=1/2, означающий, что p(X=a)=0.5 или аналогично p(X=b)=0.5 с вероятностью 50%/50% a или же b (неопределенность на максимуме). Функция энтропии находится на нулевом минимуме, когда вероятность p=1 или же p=0 с полной уверенностью (p(X=a)=1 или же p(X=a)=0 соответственно последнее подразумевает p(X=b)=1).
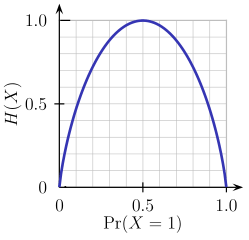
Конечно, определение энтропии можно обобщить для дискретной случайной величины X с N результатами (а не только двумя):
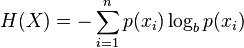
( log в формуле обычно берется логарифм к основанию 2)
Возвращаясь к нашей задаче классификации имен, давайте рассмотрим пример. Представьте, что в какой-то момент в процессе построения дерева мы рассматривали следующее разбиение:
ends-vowel
[9m,5f] <--- the [..,..] notation represents the class
/ \ distribution of instances that reached a node
=1 =0
------- -------
[3m,4f] [6m,1f]
Как видите, до раскола у нас было 9 мужчин и 5 женщин, т.е. P(m)=9/14 а также P(f)=5/14, Согласно определению энтропии:
Entropy_before = - (5/14)*log2(5/14) - (9/14)*log2(9/14) = 0.9403
Далее мы сравним ее с энтропией, вычисленной после рассмотрения разбиения, рассматривая две дочерние ветви. В левой ветке ends-vowel=1, у нас есть:
Entropy_left = - (3/7)*log2(3/7) - (4/7)*log2(4/7) = 0.9852
и правая ветвь ends-vowel=0, у нас есть:
Entropy_right = - (6/7)*log2(6/7) - (1/7)*log2(1/7) = 0.5917
Мы объединяем левую / правую энтропию, используя количество экземпляров на каждую ветвь в качестве весового коэффициента (7 экземпляров пошли влево, а 7 экземпляров - вправо), и получаем окончательную энтропию после разделения:
Entropy_after = 7/14*Entropy_left + 7/14*Entropy_right = 0.7885
Теперь, сравнивая энтропию до и после разделения, мы получаем показатель прироста информации, или сколько информации мы получили, выполнив разделение, используя эту особенность:
Information_Gain = Entropy_before - Entropy_after = 0.1518
Вы можете интерпретировать приведенный выше расчет следующим образом: end-vowels Благодаря этой функции мы смогли уменьшить неопределенность в результате прогнозирования поддерева на небольшую величину 0,1518 (измеряется в битах как единица информации).
В каждом узле дерева этот расчет выполняется для каждого объекта, а объект с наибольшим выигрышем информации выбирается для разделения жадным образом (таким образом, предпочтение отдается объектам, которые производят чистое разделение с низкой неопределенностью / энтропией). Этот процесс применяется рекурсивно от корневого узла и останавливается, когда конечный узел содержит экземпляры, имеющие один и тот же класс (нет необходимости разбивать его дальше).
Обратите внимание, что я пропустил некоторые детали, которые выходят за рамки этого поста, в том числе о том, как обрабатывать числовые функции, пропущенные значения, переоснащение и обрезку деревьев и т. Д.
Для начала было бы лучше понять the measure of information,
Как мы measure информация?
Когда случается что-то невероятное, мы говорим, что это большая новость. Кроме того, когда мы говорим что-то предсказуемое, это не очень интересно. Таким образом, чтобы определить это interesting-ness, функция должна удовлетворять
- если вероятность события равна 1 (предсказуемой), то функция дает 0
- если вероятность события близка к 0, то функция должна давать большое число
- если вероятность 0,5 события происходит, это дает
one bitинформации.
Одна естественная мера, которая удовлетворяет ограничениям
I(X) = -log_2(p)
где р - вероятность события X, И блок находится в bit, тот же битный компьютер использует. 0 или 1.
Пример 1
Честная монета
Сколько информации мы можем получить за один бросок монеты?
Ответ: -log(p) = -log(1/2) = 1 (bit)
Пример 2
Если метеор ударит Землю завтра, p=2^{-22} тогда мы можем получить 22 бита информации.
Если завтра взойдет Солнце, p ~ 1 тогда это 0 бит информации.
Энтропия
Так что, если мы возьмем ожидание на interesting-ness события YТогда это энтропия. т.е. энтропия - это ожидаемое значение интересности события.
H(Y) = E[ I(Y)]
Более формально, энтропия - это ожидаемое количество битов события.
пример
Y = 1: событие X происходит с вероятностью p
Y = 0: событие X не происходит с вероятностью 1-р
H(Y) = E[I(Y)] = p I(Y==1) + (1-p) I(Y==0)
= - p log p - (1-p) log (1-p)
Журнал базы 2 для всего журнала.
Я не могу дать вам графику, но, возможно, я могу дать четкое объяснение.
Предположим, у нас есть информационный канал, например, индикатор, который мигает один раз в день, красный или зеленый. Сколько информации это передает? Первое предположение может быть один бит в день. Но что, если мы добавим синий, чтобы у отправителя было три варианта? Нам хотелось бы иметь определенную информацию, которая может обрабатывать вещи, отличные от степеней двух, но все же быть аддитивной (способ, которым умножение количества возможных сообщений на два добавляет один бит). Мы могли бы сделать это, взяв журнал2(количество возможных сообщений), но оказалось, что есть более общий способ.
Предположим, мы вернулись к красному / зеленому, но красная лампочка перегорела (это общеизвестно), поэтому лампа всегда должна мигать зеленым. Канал теперь бесполезен, мы знаем, какая будет следующая вспышка, поэтому вспышки не передают никакой информации, никаких новостей. Сейчас мы ремонтируем лампочку, но навязываем правило, что красная лампочка не может мигать два раза подряд. Когда лампа мигает красным, мы знаем, какая будет следующая вспышка. Если вы попытаетесь отправить поток битов по этому каналу, вы обнаружите, что должны кодировать его с большим количеством вспышек, чем у вас есть битов (на самом деле на 50% больше). И если вы хотите описать последовательность вспышек, вы можете сделать это с меньшим количеством битов. То же самое применимо, если каждая вспышка независима (не зависит от контекста), но зеленые вспышки встречаются чаще, чем красные: чем больше искажение вероятности, тем меньше битов необходимо для описания последовательности и чем меньше информации она содержит, вплоть до полностью зеленый, сгоревший предел лампы.
Оказывается, есть способ измерить количество информации в сигнале, основываясь на вероятностях различных символов. Если вероятность получения символа xi равна pi, то рассмотрим величину
-log pi
Чем меньше pi, тем больше это значение. Если xi становится вдвое маловероятным, это значение увеличивается на фиксированную величину (log(2)). Это должно напомнить вам о добавлении одного бита к сообщению.
Если мы не знаем, каким будет символ (но мы знаем вероятности), тогда мы можем вычислить среднее значение этого значения, сколько мы получим, суммируя различные возможности:
I = -Σ pi log (pi)
Это информационный контент в один миг.
Красная лампочка перегорела: pred = 0, pgreen= 1, I = - (0 + 0) = 0 Красный и зеленый равновероятны: pred = 1/2, pgreen = 1/2, I = - (2 * 1/2 * log (1/2)) = log (2) Три цвета, равновероятные: pi= 1/3, I = - (3 * 1/3 * log (1/3)) = log (3) Зеленый и красный, зеленый в два раза чаще: pкрасный=1/3, pзеленый=2/3, I = -(1/3 log(1/3) + 2/3 log(2/3)) = log(3) - 2/3 журнала (2)
Это информационное содержание или энтропия сообщения. Максимально, когда разные символы равновероятны. Если вы физик, вы используете натуральный журнал, если вы специалист по информатике, вы используете журнал2 и получаете биты.
Я действительно рекомендую вам прочитать о теории информации, байесовских методах и MaxEnt. Начнем с этой книги Дэвида Маккея (свободно доступной в Интернете):
http://www.inference.phy.cam.ac.uk/mackay/itila/
Эти методы вывода на самом деле гораздо более общие, чем просто анализ текста, и я не могу придумать, как можно научиться применять это к НЛП, не изучив некоторые общие основы, содержащиеся в этой книге или других вводных книгах по машинному обучению и байесовскому методу MaxEnt. методы.
Связь между энтропией и теорией вероятности для обработки и хранения информации действительно очень глубока. Чтобы дать представление об этом, есть одна теорема Шеннона, которая гласит, что максимальный объем информации, который вы можете передать без ошибок по шумному каналу связи, равен энтропии шумового процесса. Есть также теорема, которая связывает, сколько вы можете сжать кусок данных, чтобы занять минимально возможную память на вашем компьютере с энтропией процесса, который генерировал данные.
Я не думаю, что действительно необходимо, чтобы вы изучали все эти теоремы теории коммуникации, но это невозможно изучить без изучения основ того, что такое энтропия, как она рассчитывается, как она связана с информацией и умозаключениями и т. Д....
Неофициально
энтропия - это доступность информации или знаний. Недостаток информации приведет к трудностям в прогнозировании будущего, что является высокой энтропией (прогнозирование следующего слова в текстовом анализе), а доступность информации / знаний поможет нам более реалистично прогнозировать будущее (низкая энтропия).
Соответствующая информация любого типа уменьшит энтропию и поможет нам предсказать более реалистичное будущее, что информацией может быть слово "мясо", присутствующее в предложении, или слово "мясо", которого нет. Это называется информационный прирост
Формально
энтропия это отсутствие порядка предсказуемости
Когда я реализовывал алгоритм для вычисления энтропии изображения, я нашел эти ссылки, смотрите здесь и здесь.
Это псевдокод, который я использовал, вам нужно адаптировать его для работы с текстом, а не с изображениями, но принципы должны быть такими же.
//Loop over image array elements and count occurrences of each possible
//pixel to pixel difference value. Store these values in prob_array
for j = 0, ysize-1 do $
for i = 0, xsize-2 do begin
diff = array(i+1,j) - array(i,j)
if diff lt (array_size+1)/2 and diff gt -(array_size+1)/2 then begin
prob_array(diff+(array_size-1)/2) = prob_array(diff+(array_size-1)/2) + 1
endif
endfor
//Convert values in prob_array to probabilities and compute entropy
n = total(prob_array)
entrop = 0
for i = 0, array_size-1 do begin
prob_array(i) = prob_array(i)/n
//Base 2 log of x is Ln(x)/Ln(2). Take Ln of array element
//here and divide final sum by Ln(2)
if prob_array(i) ne 0 then begin
entrop = entrop - prob_array(i)*alog(prob_array(i))
endif
endfor
entrop = entrop/alog(2)
Я получил этот код откуда-то, но я не могу найти ссылку.
Когда вы читаете книгу о NLTK, было бы интересно прочитать о модуле классификатора MaxEnt http://www.nltk.org/api/nltk.classify.html.
Для классификации интеллектуального анализа текста могут использоваться следующие этапы: предварительная обработка (токенизация, обработка паром, выбор функции с помощью информационного усиления...), преобразование в числовое значение (частота или TF-IDF) (я думаю, что это ключевой шаг, который необходимо понимать при использовании текст в качестве входных данных для алгоритма, который принимает только числа), а затем классифицировать с MaxEnt, конечно, это только пример.