Решение хаотической системы Чена методом дифференциального преобразования

Question

Я вычисляю решение хаотической системы Чена, используя метод дифференциального преобразования. Код, который я использую:

x=zeros(1,7);
x(1)=-0.1;
y=zeros(1,7);
y(1)=0.5;
z=zeros(1,7);
z(1)=-0.6;
for k=0:5
    x(k+2)=(40*gamma(1+k)/gamma(2+k))*(y(k+1)-x(k+1));
    sum=0;
    for l=0:k
        sum=sum+x(l+1)*z(k+1-l);
    end
    y(k+2)=(gamma(1+k)/gamma(2+k))*(-12*x(k+1)-sum+28*y(k+1));
    sum=0;
    for l=0:k
        sum=sum+x(l+1)*y(k+1-l);
    end
    z(k+2)=(gamma(1+k)/(1+k))*(sum-3*z(k+1));
end
s=fliplr(x);
t=0:0.05:2;
a=polyval(s,t);
plot(t,a)

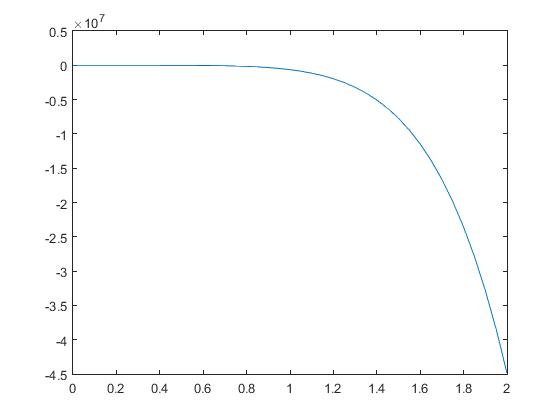
Что этот код делает, это рассчитать x(k), y(k) а также z(k) это коэффициенты полинома, аппроксимирующего решение. Решение x(t) = sum_0^infinity x(k)t^kи аналогично другим. Но этот код не дает желаемого результата хаотической последовательности граф x(t) что я получаю это:

Answer 1

Это не ответ, а более четкая и правильная (программно говоря) запись вашего цикла:

for k = 1:6
    x(k+1)=(40*1/k)*(y(k)-x(k));
    temp_sum = sum(x(1:k).*z(k:-1:1),2);
    y(k+1) = (1/k)*(-12*x(k)-temp_sum+28*y(k));
    temp_sum = sum(x(1:k).*y(k:-1:1),2);
    z(k+1) = (1/k)*(temp_sum-3*z(k));
end

Самым важным вопросом здесь не является перегрузка встроенной функции sum (Я заменил его на temp_sum, Другие вещи включают векторизацию внутренних циклов (используя sum...), индексация начинается с 1 (вместо записи k+1 все время) и удаление ненужных звонков gamma (gamma(k)/gamma(k+1) знак равно 1/k).