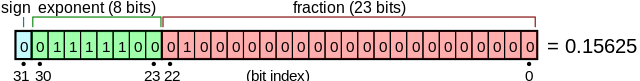Что такое субнормальное число с плавающей точкой?
Ссылочная страница isnormal() сообщает:
Определяет, является ли данное число с плавающей точкой arg нормальным, то есть не является ли оно нулевым, субнормальным, бесконечным или NaN.
Число ноль, бесконечность или NaN ясно, что это значит. Но это также говорит о ненормальном. Когда число ненормальное?
3 ответа
В стандарте IEEE754 числа с плавающей запятой представлены в виде двоичного научного обозначения, x = M × 2e. Здесь М - мантисса, а е - показатель степени. Математически вы всегда можете выбрать показатель степени так, чтобы 1 ≤ M <2. * Однако, поскольку в компьютерном представлении показатель степени может иметь только конечный диапазон, существуют некоторые числа, которые больше нуля, но меньше 1,0 × 2 e.мин. Эти числа являются субнормальными или денормальными.
Практически, мантисса хранится без начального 1, так как всегда есть начальный 1, за исключением субнормальных чисел (и нуля). Таким образом, интерпретация заключается в том, что если показатель степени неминимален, существует неявное ведение 1, а если показатель минимален, то нет, а число является субнормальным.
*) В более общем смысле 1 ≤ M < B для любой научной записи Base-B.
Основы IEEE 754
Сначала давайте рассмотрим основы IEEE 754 номера организованы.
Мы сконцентрируемся на одинарной точности (32-битной), но все можно сразу обобщить до другой точности.
Формат такой:
- 1 бит: знак
- 8 бит: показатель степени
- 23 бита: дробь
Или если вам нравятся картинки:
Знак прост: 0 положительно, 1 отрицательно, конец истории.
Экспонента имеет длину 8 битов, поэтому она колеблется от 0 до 255.
Экспонента называется смещенной, потому что она имеет смещение -127Например:
0 == special case: zero or subnormal, explained below
1 == 2 ^ -126
...
125 == 2 ^ -2
126 == 2 ^ -1
127 == 2 ^ 0
128 == 2 ^ 1
129 == 2 ^ 2
...
254 == 2 ^ 127
255 == special case: infinity and NaN
Ведущая битовая конвенция
При разработке IEEE 754 инженеры заметили, что все числа, кроме 0.0есть один 1 в двоичном виде в качестве первой цифры
Например:
25.0 == (binary) 11001 == 1.1001 * 2^4
0.625 == (binary) 0.101 == 1.01 * 2^-1
оба начинают с этого раздражающего 1. часть.
Поэтому было бы расточительно, чтобы эта цифра занимала один бит точности почти каждого отдельного числа.
По этой причине они создали "ведущее битовое соглашение":
всегда предполагайте, что число начинается с одного
Но тогда как бороться с 0.0? Ну, они решили создать исключение:
- если показатель равен 0
- и фракция равна 0
- тогда число представляет плюс или минус
0.0
так что байты 00 00 00 00 также представляют 0.0, который выглядит хорошо.
Если бы мы рассматривали только эти правила, то наименьшее ненулевое число, которое может быть представлено:
- показатель степени: 0
- фракция: 1
который выглядит примерно так в шестнадцатеричной дроби из-за соглашения о ведущих битах:
1.000002 * 2 ^ (-127)
где .000002 22 нуля с 1 в конце.
Мы не можем взять fraction = 0иначе это число будет 0.0,
Но затем инженеры, которые также имели острый художественный смысл, подумали: разве это не уродливо? Что мы прыгаем с прямой 0.0 к чему-то, что даже не является правильной степенью 2? Разве мы не можем представить даже меньшие числа?
Субнормальные числа
Инженеры немного почесали головы и вернулись, как обычно, с еще одной хорошей идеей. Что если мы создадим новое правило:
Если показатель равен 0, то:
- ведущий бит становится 0
- показатель степени фиксируется на -126 (не -127, как если бы у нас не было этого исключения)
Такие числа называются субнормальными числами (или ненормальными числами, которые являются синонимами).
Это правило сразу подразумевает, что число такое, что:
- показатель степени: 0
- фракция: 0
является 0.0, что довольно элегантно, поскольку означает, что нужно следить за одним правилом.
Так 0.0 на самом деле это ненормальное число в соответствии с нашим определением!
Тогда с этим новым правилом наименьшее не субнормальное число:
- показатель степени: 1 (0 будет субнормальным)
- фракция: 0
который представляет:
1.0 * 2 ^ (-126)
Тогда наибольшее субнормальное число:
- показатель степени: 0
- фракция: 0x7FFFFF (23 бита 1)
что равно:
0.FFFFFE * 2 ^ (-126)
где .FFFFFE еще раз 23 бита один справа от точки.
Это довольно близко к наименьшему не субнормальному числу, которое звучит вменяемым.
И наименьшее ненулевое субнормальное число:
- показатель степени: 0
- фракция: 1
что равно:
0.000002 * 2 ^ (-126)
который также выглядит довольно близко к 0.0!
Не имея возможности найти какой-либо разумный способ представления чисел, меньших этого, инженеры были счастливы и вернулись к просмотру фотографий кошек в Интернете или к тому, чем они занимались в 70-х годах.
Как видите, субнормальные числа делают компромисс между точностью и длиной представления.
Как самый экстремальный пример, самое маленькое ненулевое субнормальное:
0.000002 * 2 ^ (-126)
имеет по существу точность одного бита вместо 32-битных. Например, если мы разделим это на два:
0.000002 * 2 ^ (-126) / 2
мы на самом деле достигаем 0.0 именно так!
Runnable C пример
Теперь давайте поиграем с реальным кодом, чтобы проверить нашу теорию.
Почти во всех современных и настольных компьютерах, C float представляет числа с плавающей запятой IEEE 754 одинарной точности.
В частности, это касается моего ноутбука Ubuntu 18.04 amd64 Lenovo P51.
С этим допущением все утверждения передаются следующей программе:
subnormal.c
#if __STDC_VERSION__ < 201112L
#error C11 required
#endif
#ifndef __STDC_IEC_559__
#error IEEE 754 not implemented
#endif
#include <assert.h>
#include <float.h> /* FLT_HAS_SUBNORM */
#include <inttypes.h>
#include <math.h> /* isnormal */
#include <stdlib.h>
#include <stdio.h>
#if FLT_HAS_SUBNORM != 1
#error float does not have subnormal numbers
#endif
typedef struct {
uint32_t sign, exponent, fraction;
} Float32;
Float32 float32_from_float(float f) {
uint32_t bytes;
Float32 float32;
bytes = *(uint32_t*)&f;
float32.fraction = bytes & 0x007FFFFF;
bytes >>= 23;
float32.exponent = bytes & 0x000000FF;
bytes >>= 8;
float32.sign = bytes & 0x000000001;
bytes >>= 1;
return float32;
}
float float_from_bytes(
uint32_t sign,
uint32_t exponent,
uint32_t fraction
) {
uint32_t bytes;
bytes = 0;
bytes |= sign;
bytes <<= 8;
bytes |= exponent;
bytes <<= 23;
bytes |= fraction;
return *(float*)&bytes;
}
int float32_equal(
float f,
uint32_t sign,
uint32_t exponent,
uint32_t fraction
) {
Float32 float32;
float32 = float32_from_float(f);
return
(float32.sign == sign) &&
(float32.exponent == exponent) &&
(float32.fraction == fraction)
;
}
void float32_print(float f) {
Float32 float32 = float32_from_float(f);
printf(
"%" PRIu32 " %" PRIu32 " %" PRIu32 "\n",
float32.sign, float32.exponent, float32.fraction
);
}
int main(void) {
/* Basic examples. */
assert(float32_equal(0.5f, 0, 126, 0));
assert(float32_equal(1.0f, 0, 127, 0));
assert(float32_equal(2.0f, 0, 128, 0));
assert(isnormal(0.5f));
assert(isnormal(1.0f));
assert(isnormal(2.0f));
/* Quick review of C hex floating point literals. */
assert(0.5f == 0x1.0p-1f);
assert(1.0f == 0x1.0p0f);
assert(2.0f == 0x1.0p1f);
/* Sign bit. */
assert(float32_equal(-0.5f, 1, 126, 0));
assert(float32_equal(-1.0f, 1, 127, 0));
assert(float32_equal(-2.0f, 1, 128, 0));
assert(isnormal(-0.5f));
assert(isnormal(-1.0f));
assert(isnormal(-2.0f));
/* The special case of 0.0 and -0.0. */
assert(float32_equal( 0.0f, 0, 0, 0));
assert(float32_equal(-0.0f, 1, 0, 0));
assert(!isnormal( 0.0f));
assert(!isnormal(-0.0f));
assert(0.0f == -0.0f);
/* ANSI C defines FLT_MIN as the smallest non-subnormal number. */
assert(FLT_MIN == 0x1.0p-126f);
assert(float32_equal(FLT_MIN, 0, 1, 0));
assert(isnormal(FLT_MIN));
/* The largest subnormal number. */
float largest_subnormal = float_from_bytes(0, 0, 0x7FFFFF);
assert(largest_subnormal == 0x0.FFFFFEp-126f);
assert(largest_subnormal < FLT_MIN);
assert(!isnormal(largest_subnormal));
/* The smallest non-zero subnormal number. */
float smallest_subnormal = float_from_bytes(0, 0, 1);
assert(smallest_subnormal == 0x0.000002p-126f);
assert(0.0f < smallest_subnormal);
assert(!isnormal(smallest_subnormal));
return EXIT_SUCCESS;
}
Скомпилируйте и запустите с:
gcc -ggdb3 -O0 -std=c11 -Wall -Wextra -Wpedantic -Werror -o subnormal.out subnormal.c
./subnormal.out
Визуализация
Это всегда хорошая идея иметь геометрическую интуицию о том, что мы изучаем, так что здесь.
Если мы построим числа IEEE 754 с плавающей запятой в строке для каждого данного показателя степени, это будет выглядеть примерно так:
+---+-------+---------------+-------------------------------+
exponent |126| 127 | 128 | 129 |
+---+-------+---------------+-------------------------------+
| | | | |
v v v v v
-------------------------------------------------------------
floats ***** * * * * * * * * * * * *
-------------------------------------------------------------
^ ^ ^ ^ ^
| | | | |
0.5 1.0 2.0 4.0 8.0
Отсюда видно, что для каждого показателя степени:
- между представленными числами нет совпадений
- для каждого показателя у нас одинаковое число 2^32 (здесь представлено 4
*) - точки одинаково разнесены для данного показателя
- большие показатели охватывают большие диапазоны, но с более широкими точками
Теперь давайте опустим это до степени 0.
Без субнормалей это будет выглядеть гипотетически:
+---+---+-------+---------------+-------------------------------+
exponent | ? | 0 | 1 | 2 | 3 |
+---+---+-------+---------------+-------------------------------+
| | | | | |
v v v v v v
-----------------------------------------------------------------
floats * ***** * * * * * * * * * * * *
-----------------------------------------------------------------
^ ^ ^ ^ ^ ^
| | | | | |
0 | 2^-126 2^-125 2^-124 2^-123
|
2^-127
С субнормалами:
+-------+-------+---------------+-------------------------------+
exponent | 0 | 1 | 2 | 3 |
+-------+-------+---------------+-------------------------------+
| | | | |
v v v v v
-----------------------------------------------------------------
floats * * * * * * * * * * * * * * * * *
-----------------------------------------------------------------
^ ^ ^ ^ ^ ^
| | | | | |
0 | 2^-126 2^-125 2^-124 2^-123
|
2^-127
Сравнивая два графика, мы видим, что:
субнормалы удваивают длину диапазона экспоненты
0, от[2^-127, 2^-126)в[0, 2^-126)Расстояние между поплавками в субнормальном диапазоне такое же, как и для
[0, 2^-126),диапазон
[2^-127, 2^-126)имеет половину количества баллов, которое было бы без субнормалей.Половина этих точек идет, чтобы заполнить другую половину диапазона.
диапазон
[0, 2^-127)имеет несколько точек с субнормалами, но ни одна без.Это отсутствие очков в
[0, 2^-127)не очень элегантно и является основной причиной существования субнормалей!поскольку точки расположены на равном расстоянии:
- диапазон
[2^-128, 2^-127)имеет половину очков, чем[2^-127, 2^-126)-[2^-129, 2^-128)имеет половину очков, чем[2^-128, 2^-127) - и так далее
Это то, что мы имеем в виду, говоря, что субнормалы - это компромисс между размером и точностью.
- диапазон
Реализации
x86_64 реализует IEEE 754 непосредственно на аппаратном обеспечении, которому код C переводит.
TODO: какие-нибудь заметные примеры современного оборудования, у которого нет субнормалов?
TODO: любая реализация позволяет контролировать его во время выполнения?
Субнормалы в некоторых реализациях кажутся менее быстрыми, чем нормальные: почему изменение от 0,1f до 0 снижает производительность в 10 раз?
Бесконечность и NaN
Вот краткий пример выполнения: Диапазоны типа данных с плавающей запятой в C?
С http://blogs.oracle.com/d/entry/subnormal_numbers:
Существует несколько способов представления одного и того же числа, используя в качестве примера десятичное число: число 0,1 может быть представлено как 1*10-1 или 0,1*100 или даже 0,01*10. Стандарт диктует, что числа всегда сохраняются с первый бит как единое целое. В десятичном виде это соответствует примеру 1*10-1.
Теперь предположим, что самый низкий показатель, который может быть представлен, равен -100. Таким образом, наименьшее число, которое может быть представлено в нормальной форме, составляет 1*10-100. Однако, если мы ослабим ограничение на то, что ведущий бит равен единице, то мы можем фактически представить меньшие числа в одном и том же пространстве. Взяв десятичный пример, мы могли бы представить 0,1*10-100. Это называется субнормальным числом. Цель получения субнормальных чисел состоит в том, чтобы сгладить разрыв между наименьшим нормальным числом и нулем.
Очень важно понимать, что субнормальные числа представлены с меньшей точностью, чем нормальные числа. Фактически, они обменивают уменьшенную точность на их меньший размер. Следовательно, вычисления, использующие субнормальные числа, не будут иметь такую же точность, как вычисления для нормальных чисел. Таким образом, приложение, которое выполняет существенные вычисления над ненормальными числами, вероятно, стоит исследовать, чтобы увидеть, приведет ли изменение масштаба (т.е. умножение чисел к некоторому коэффициенту масштабирования) меньше субнормалей и более точных результатов.