Создать тепловую карту в MatPlotLib, используя набор данных разброса
У меня есть набор точек данных X,Y (около 10 тыс.), Которые легко построить в виде точечной диаграммы, но которые я хотел бы представить в виде тепловой карты.
Я просмотрел примеры в MatPlotLib, и все они, похоже, уже начинаются со значений ячеек тепловой карты для генерации изображения.
Есть ли метод, который преобразует группу x,y, все разные, в тепловую карту (где зоны с более высокой частотой x, y будут "теплее")?
13 ответов
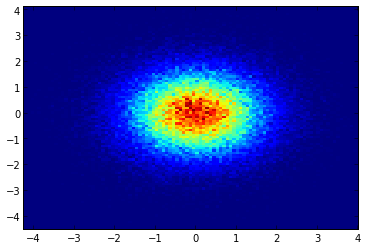
Если вы не хотите шестиугольники, вы можете использовать Numpy's histogram2d функция:
import numpy as np
import numpy.random
import matplotlib.pyplot as plt
# Generate some test data
x = np.random.randn(8873)
y = np.random.randn(8873)
heatmap, xedges, yedges = np.histogram2d(x, y, bins=50)
extent = [xedges[0], xedges[-1], yedges[0], yedges[-1]]
plt.clf()
plt.imshow(heatmap.T, extent=extent, origin='lower')
plt.show()
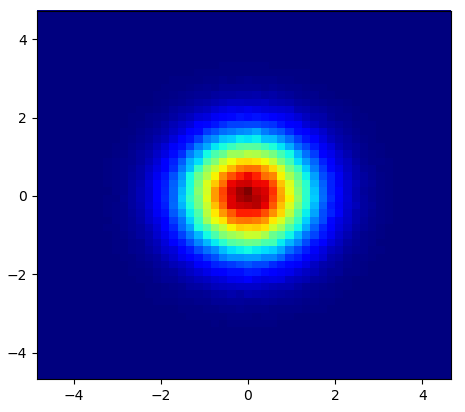
Это составляет тепловую карту 50x50. Если вы хотите, скажем, 512x384, вы можете поставить bins=(512, 384) в призыве к histogram2d,
Пример: 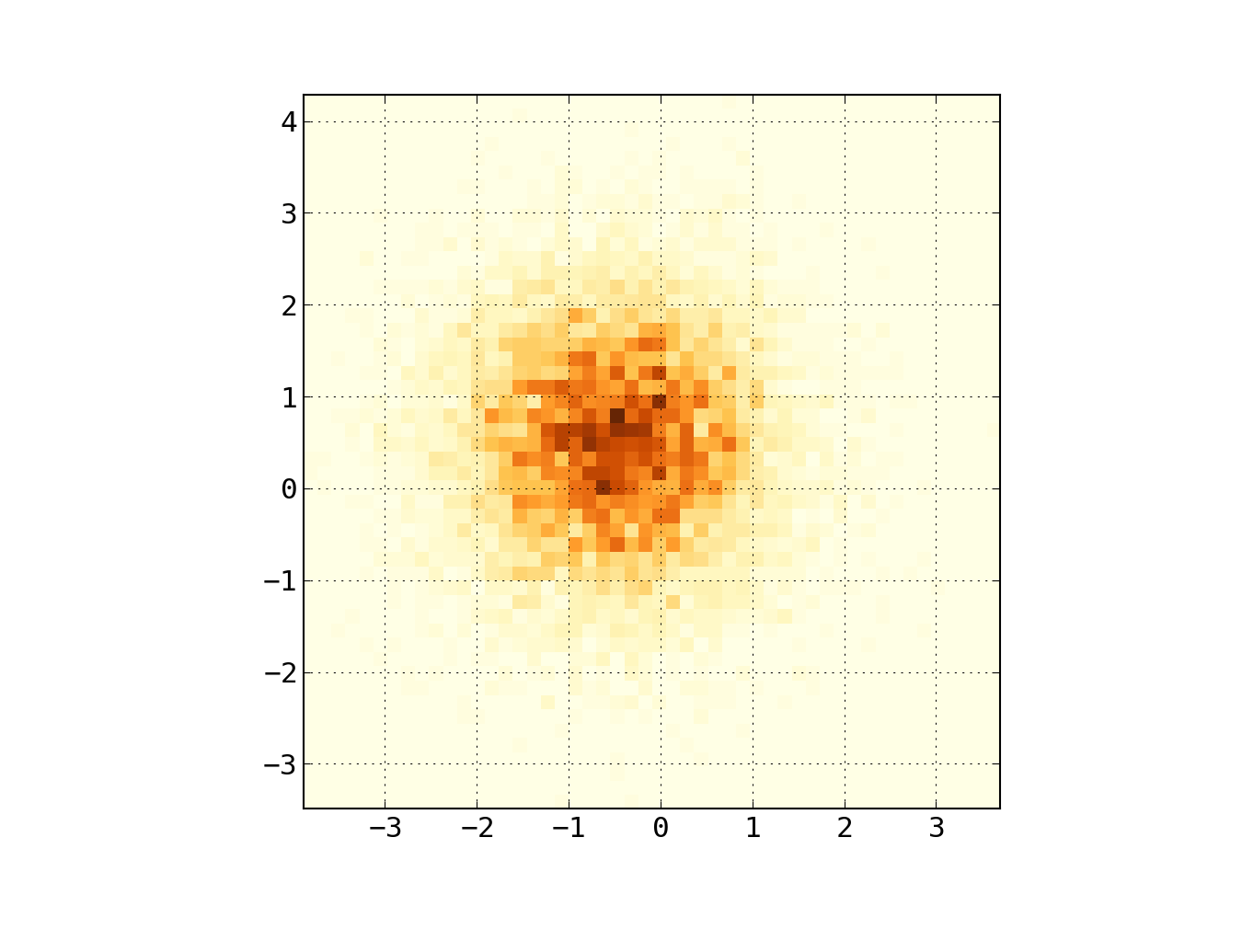
В лексиконе Matplotlib, я думаю, вы хотите сюжет в гексбине.
Если вы не знакомы с этим типом графика, это просто двумерная гистограмма, в которой плоскость xy тесселяется регулярной сеткой шестиугольников.
Таким образом, из гистограммы вы можете просто подсчитать количество точек, попадающих в каждый шестиугольник, дискретизировать область построения как набор окон, назначить каждую точку одному из этих окон; наконец, сопоставьте окна с массивом цветов, и у вас получится шестнадцатеричная диаграмма.
Хотя шестиугольники используются реже, чем, например, круги или квадраты, этот выбор является лучшим выбором для геометрии контейнера для сбора мусора, он интуитивно понятен:
шестиугольники имеют симметрию ближайшего соседа (например, квадратные ячейки не имеют, например, расстояние от точки на границе квадрата до точки внутри этого квадрата не везде одинаково) и
шестиугольник - это самый высокий n-многоугольник, который дает регулярную плоскую тесселяцию (т. е. вы можете смело смоделировать пол на кухне плитками шестиугольной формы, потому что у вас не будет пустого пространства между плитками, когда вы закончите - это не так все остальные высшие n, n >= 7, полигоны).
(Matplotlib использует термин hexbin plot; так же (AFAIK) - все библиотеки построения графиков для R; все еще я не знаю, является ли это общепринятым термином для графиков этого типа, хотя я подозреваю, что, вероятно, учитывая, что hexbin является коротким для гексагонального биннинга, который описывает важный этап подготовки данных для отображения.)
from matplotlib import pyplot as PLT
from matplotlib import cm as CM
from matplotlib import mlab as ML
import numpy as NP
n = 1e5
x = y = NP.linspace(-5, 5, 100)
X, Y = NP.meshgrid(x, y)
Z1 = ML.bivariate_normal(X, Y, 2, 2, 0, 0)
Z2 = ML.bivariate_normal(X, Y, 4, 1, 1, 1)
ZD = Z2 - Z1
x = X.ravel()
y = Y.ravel()
z = ZD.ravel()
gridsize=30
PLT.subplot(111)
# if 'bins=None', then color of each hexagon corresponds directly to its count
# 'C' is optional--it maps values to x-y coordinates; if 'C' is None (default) then
# the result is a pure 2D histogram
PLT.hexbin(x, y, C=z, gridsize=gridsize, cmap=CM.jet, bins=None)
PLT.axis([x.min(), x.max(), y.min(), y.max()])
cb = PLT.colorbar()
cb.set_label('mean value')
PLT.show()
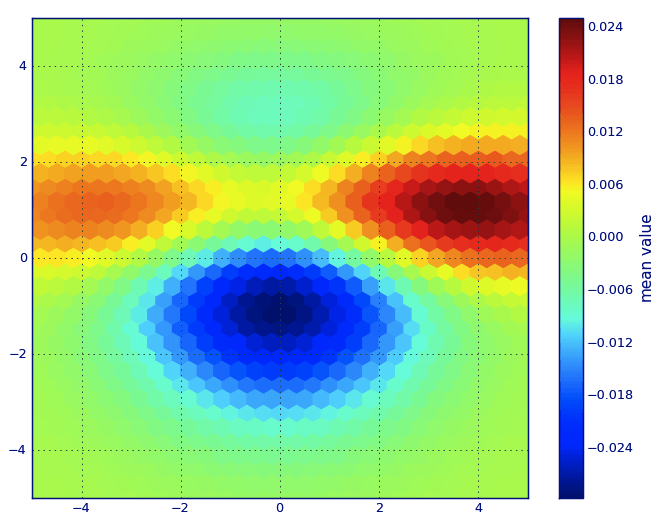
Изменить: Для лучшего приближения ответа Алехандро, см. Ниже.
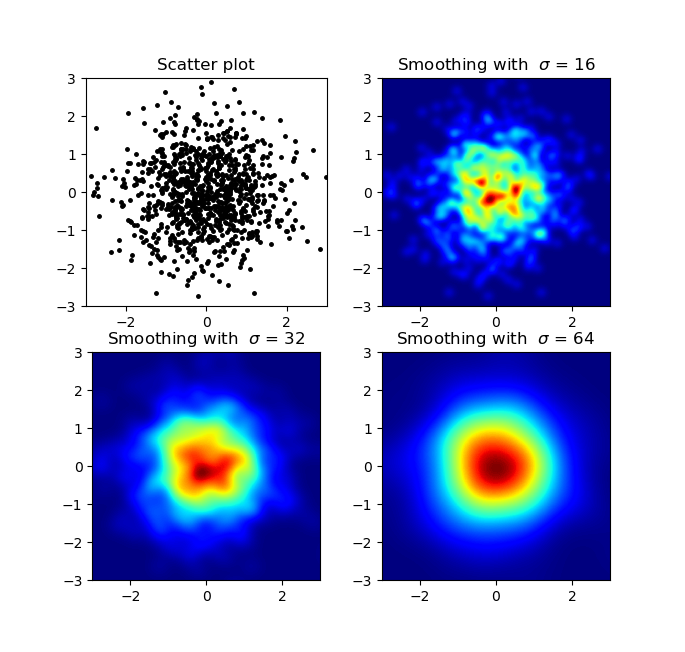
Я знаю, что это старый вопрос, но я хотел добавить кое-что к ответу Алехандро: если вы хотите получить хорошее сглаженное изображение без использования py-sphviewer, вы можете вместо этого использовать np.histogram2d и применить фильтр Гаусса (из scipy.ndimage.filters) к тепловой карте:
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.cm as cm
from scipy.ndimage.filters import gaussian_filter
def myplot(x, y, s, bins=1000):
heatmap, xedges, yedges = np.histogram2d(x, y, bins=bins)
heatmap = gaussian_filter(heatmap, sigma=s)
extent = [xedges[0], xedges[-1], yedges[0], yedges[-1]]
return heatmap.T, extent
fig, axs = plt.subplots(2, 2)
# Generate some test data
x = np.random.randn(1000)
y = np.random.randn(1000)
sigmas = [0, 16, 32, 64]
for ax, s in zip(axs.flatten(), sigmas):
if s == 0:
ax.plot(x, y, 'k.', markersize=5)
ax.set_title("Scatter plot")
else:
img, extent = myplot(x, y, s)
ax.imshow(img, extent=extent, origin='lower', cmap=cm.jet)
ax.set_title("Smoothing with $\sigma$ = %d" % s)
plt.show()
Производит:
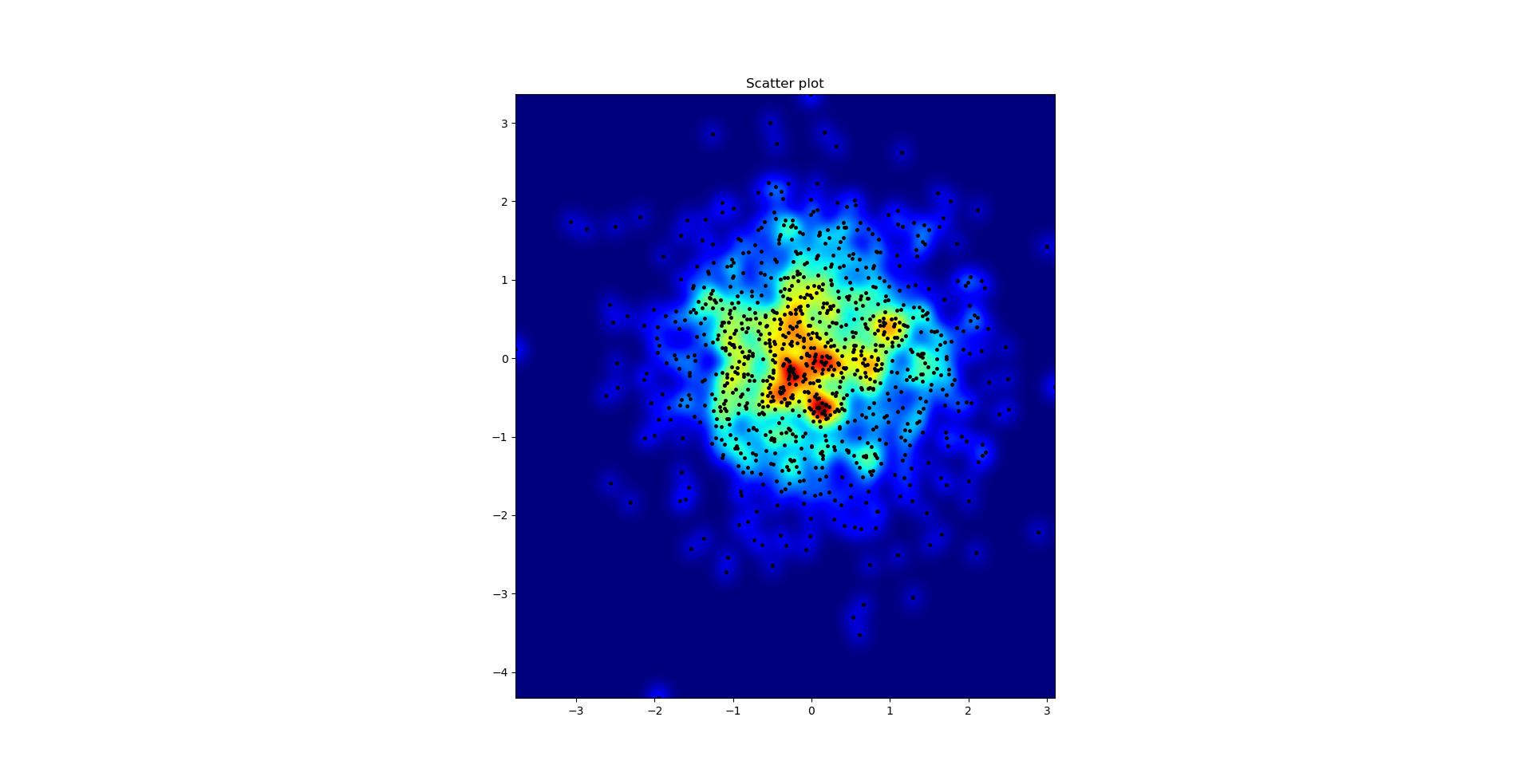
Диаграмма рассеяния и s=16, нанесенные поверх друг друга для Агапе Гальо (нажмите для лучшего просмотра):
Одно отличие, которое я заметил с моим подходом гауссовского фильтра и подходом Алехандро, было то, что его метод показывает локальные структуры намного лучше, чем мой. Поэтому я реализовал простой метод ближайшего соседа на уровне пикселей. Этот метод рассчитывает для каждого пикселя обратную сумму расстояний n ближайшие точки в данных. Этот метод с высоким разрешением довольно дорогой в вычислительном отношении, и я думаю, что есть более быстрый способ, поэтому дайте мне знать, если у вас есть какие-либо улучшения. Во всяком случае, вот код:
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.cm as cm
def data_coord2view_coord(p, vlen, pmin, pmax):
dp = pmax - pmin
dv = (p - pmin) / dp * vlen
return dv
def nearest_neighbours(xs, ys, reso, n_neighbours):
im = np.zeros([reso, reso])
extent = [np.min(xs), np.max(xs), np.min(ys), np.max(ys)]
xv = data_coord2view_coord(xs, reso, extent[0], extent[1])
yv = data_coord2view_coord(ys, reso, extent[2], extent[3])
for x in range(reso):
for y in range(reso):
xp = (xv - x)
yp = (yv - y)
d = np.sqrt(xp**2 + yp**2)
im[y][x] = 1 / np.sum(d[np.argpartition(d.ravel(), n_neighbours)[:n_neighbours]])
return im, extent
n = 1000
xs = np.random.randn(n)
ys = np.random.randn(n)
resolution = 250
fig, axes = plt.subplots(2, 2)
for ax, neighbours in zip(axes.flatten(), [0, 16, 32, 64]):
if neighbours == 0:
ax.plot(xs, ys, 'k.', markersize=2)
ax.set_aspect('equal')
ax.set_title("Scatter Plot")
else:
im, extent = nearest_neighbours(xs, ys, resolution, neighbours)
ax.imshow(im, origin='lower', extent=extent, cmap=cm.jet)
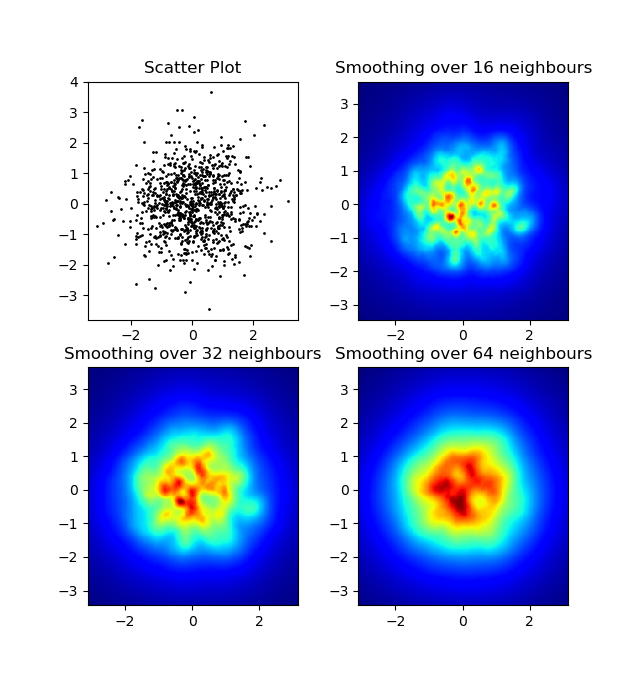
ax.set_title("Smoothing over %d neighbours" % neighbours)
ax.set_xlim(extent[0], extent[1])
ax.set_ylim(extent[2], extent[3])
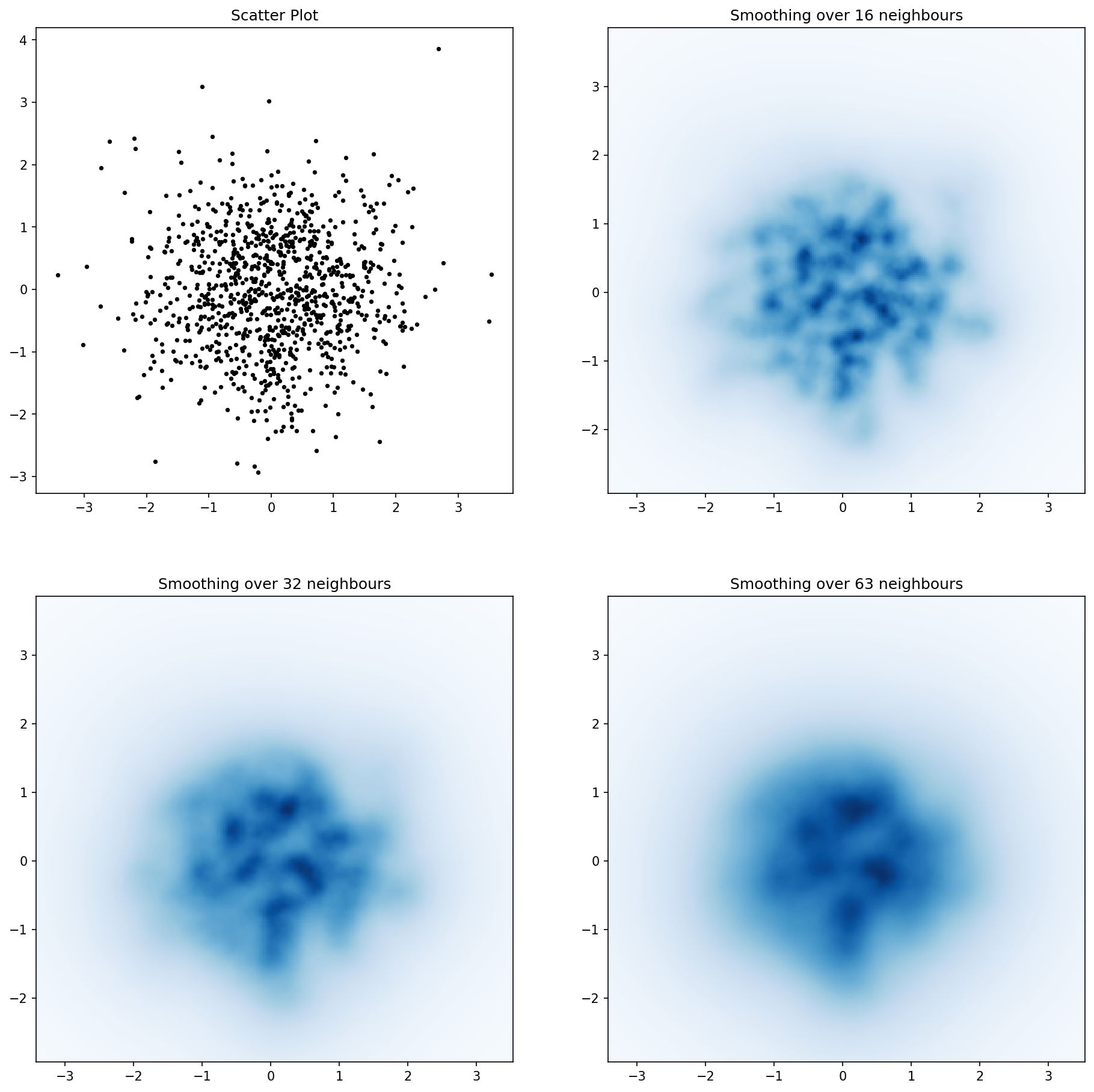
plt.show()
Результат:
Вместо того, чтобы использовать np.hist2d, который обычно генерирует довольно некрасивые гистограммы, я хотел бы переработать py-sphviewer, пакет python для рендеринга симуляций частиц с использованием адаптивного сглаживающего ядра, который можно легко установить из pip (см. Документацию веб-страницы). Рассмотрим следующий код, основанный на примере:
import numpy as np
import numpy.random
import matplotlib.pyplot as plt
import sphviewer as sph
def myplot(x, y, nb=32, xsize=500, ysize=500):
xmin = np.min(x)
xmax = np.max(x)
ymin = np.min(y)
ymax = np.max(y)
x0 = (xmin+xmax)/2.
y0 = (ymin+ymax)/2.
pos = np.zeros([3, len(x)])
pos[0,:] = x
pos[1,:] = y
w = np.ones(len(x))
P = sph.Particles(pos, w, nb=nb)
S = sph.Scene(P)
S.update_camera(r='infinity', x=x0, y=y0, z=0,
xsize=xsize, ysize=ysize)
R = sph.Render(S)
R.set_logscale()
img = R.get_image()
extent = R.get_extent()
for i, j in zip(xrange(4), [x0,x0,y0,y0]):
extent[i] += j
print extent
return img, extent
fig = plt.figure(1, figsize=(10,10))
ax1 = fig.add_subplot(221)
ax2 = fig.add_subplot(222)
ax3 = fig.add_subplot(223)
ax4 = fig.add_subplot(224)
# Generate some test data
x = np.random.randn(1000)
y = np.random.randn(1000)
#Plotting a regular scatter plot
ax1.plot(x,y,'k.', markersize=5)
ax1.set_xlim(-3,3)
ax1.set_ylim(-3,3)
heatmap_16, extent_16 = myplot(x,y, nb=16)
heatmap_32, extent_32 = myplot(x,y, nb=32)
heatmap_64, extent_64 = myplot(x,y, nb=64)
ax2.imshow(heatmap_16, extent=extent_16, origin='lower', aspect='auto')
ax2.set_title("Smoothing over 16 neighbors")
ax3.imshow(heatmap_32, extent=extent_32, origin='lower', aspect='auto')
ax3.set_title("Smoothing over 32 neighbors")
#Make the heatmap using a smoothing over 64 neighbors
ax4.imshow(heatmap_64, extent=extent_64, origin='lower', aspect='auto')
ax4.set_title("Smoothing over 64 neighbors")
plt.show()
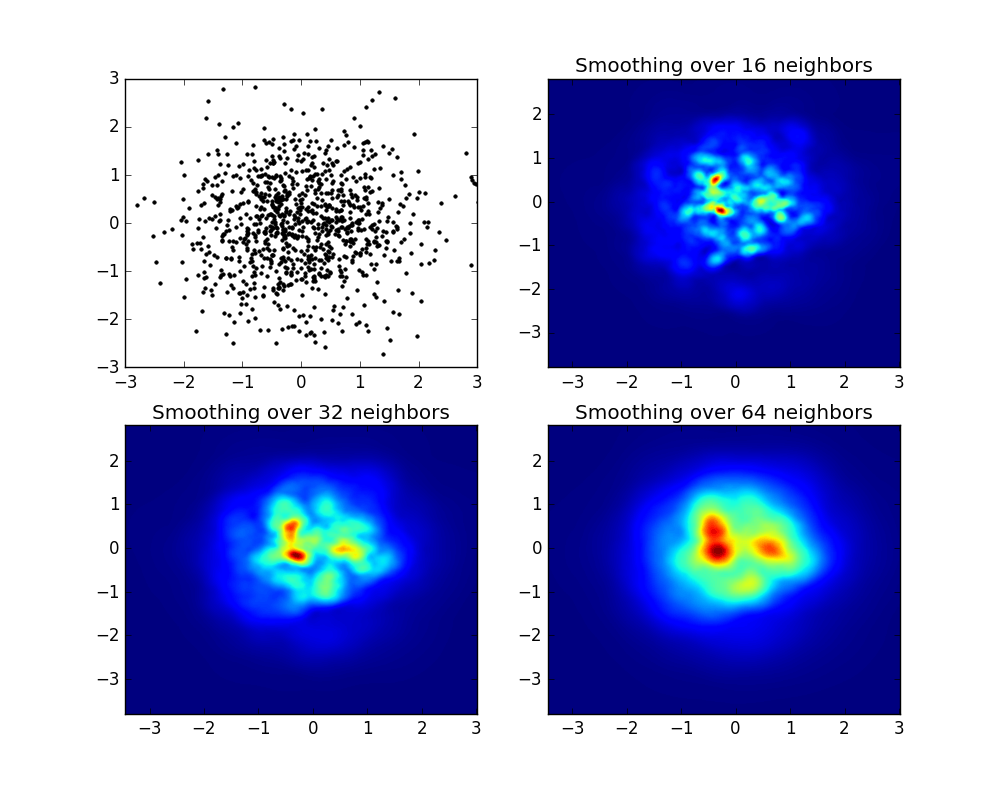
который производит следующее изображение:
Как видите, изображения выглядят довольно красиво, и мы можем определить различные подструктуры на нем. Эти изображения построены с распределением заданного веса для каждой точки в определенной области, определенной длиной сглаживания, которая, в свою очередь, определяется расстоянием до ближайшего соседа nb (в качестве примеров я выбрал 16, 32 и 64). Таким образом, области с более высокой плотностью обычно распространяются на более мелкие области по сравнению с областями с более низкой плотностью.
Функция myplot - это просто очень простая функция, которую я написал для того, чтобы передать данные x, y py-sphviewer для выполнения магии.
Если вы используете 1.2.x
х = рандн (100000) у = рандн (100000) hist2d(х, у, бункеров =100);
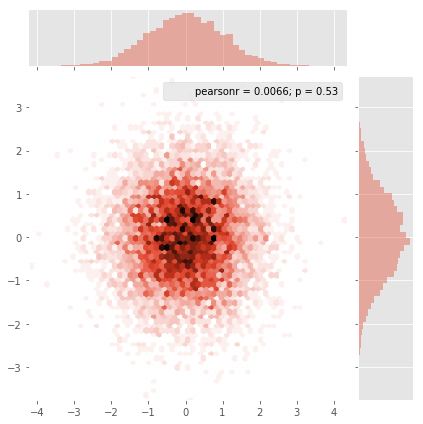
У Seaborn теперь есть функция jointplot, которая должна хорошо работать здесь:
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
# Generate some test data
x = np.random.randn(8873)
y = np.random.randn(8873)
sns.jointplot(x=x, y=y, kind='hex')
plt.show()
Вот подход Джурджи к отличному ближайшему соседу, но реализованный с использованием scipy.cKDTree. В моих тестах это примерно в 100 раз быстрее.
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.cm as cm
from scipy.spatial import cKDTree
def data_coord2view_coord(p, resolution, pmin, pmax):
dp = pmax - pmin
dv = (p - pmin) / dp * resolution
return dv
n = 1000
xs = np.random.randn(n)
ys = np.random.randn(n)
resolution = 250
extent = [np.min(xs), np.max(xs), np.min(ys), np.max(ys)]
xv = data_coord2view_coord(xs, resolution, extent[0], extent[1])
yv = data_coord2view_coord(ys, resolution, extent[2], extent[3])
def kNN2DDens(xv, yv, resolution, neighbours, dim=2):
"""
"""
# Create the tree
tree = cKDTree(np.array([xv, yv]).T)
# Find the closest nnmax-1 neighbors (first entry is the point itself)
grid = np.mgrid[0:resolution, 0:resolution].T.reshape(resolution**2, dim)
dists = tree.query(grid, neighbours)
# Inverse of the sum of distances to each grid point.
inv_sum_dists = 1. / dists[0].sum(1)
# Reshape
im = inv_sum_dists.reshape(resolution, resolution)
return im
fig, axes = plt.subplots(2, 2, figsize=(15, 15))
for ax, neighbours in zip(axes.flatten(), [0, 16, 32, 63]):
if neighbours == 0:
ax.plot(xs, ys, 'k.', markersize=5)
ax.set_aspect('equal')
ax.set_title("Scatter Plot")
else:
im = kNN2DDens(xv, yv, resolution, neighbours)
ax.imshow(im, origin='lower', extent=extent, cmap=cm.Blues)
ax.set_title("Smoothing over %d neighbours" % neighbours)
ax.set_xlim(extent[0], extent[1])
ax.set_ylim(extent[2], extent[3])
plt.savefig('new.png', dpi=150, bbox_inches='tight')
И первоначальный вопрос был... как преобразовать значения разброса в значения сетки, верно?histogram2d действительно рассчитывает частоту на ячейку, однако, если у вас есть данные на ячейку, отличные от частоты, вам потребуется дополнительная работа.
x = data_x # between -10 and 4, log-gamma of an svc
y = data_y # between -4 and 11, log-C of an svc
z = data_z #between 0 and 0.78, f1-values from a difficult dataset
Итак, у меня есть набор данных с Z-результатами для координат X и Y. Однако я вычислял несколько точек за пределами области интереса (большие пробелы) и кучу точек в небольшой области интереса.
Да, здесь становится сложнее, но и веселее. Некоторые библиотеки (извините):
from matplotlib import pyplot as plt
from matplotlib import cm
import numpy as np
from scipy.interpolate import griddata
Сегодня pyplot - мой графический движок, cm - это диапазон цветовых карт с некоторым интересным выбором. numpy для расчетов и griddata для привязки значений к фиксированной сетке.
Последнее важно, особенно потому, что частота точек xy не одинаково распределена в моих данных. Во-первых, давайте начнем с некоторых границ, подходящих для моих данных и произвольного размера сетки. Исходные данные также имеют точки данных вне этих границ x и y.
#determine grid boundaries
gridsize = 500
x_min = -8
x_max = 2.5
y_min = -2
y_max = 7
Итак, мы определили сетку с 500 пикселями между минимальным и максимальным значениями x и y.
По моим данным, существует более 500 доступных значений в области повышенного интереса; тогда как в области низкого интереса нет даже 200 значений в общей сетке; между графическими границами x_min а также x_max там еще меньше.
Поэтому для получения хорошей картины задача состоит в том, чтобы получить среднее значение для высоких процентных значений и заполнить пробелы в других местах.
Я сейчас определяю свою сетку. Для каждой пары хх-уу я хочу иметь цвет.
xx = np.linspace(x_min, x_max, gridsize) # array of x values
yy = np.linspace(y_min, y_max, gridsize) # array of y values
grid = np.array(np.meshgrid(xx, yy.T))
grid = grid.reshape(2, grid.shape[1]*grid.shape[2]).T
Почему странная форма? scipy.griddata хочет иметь форму (n, D).
Griddata рассчитывает одно значение для каждой точки в сетке с помощью предварительно определенного метода. Я выбираю "ближайший" - пустые точки сетки будут заполнены значениями от ближайшего соседа. Это выглядит так, как будто области с меньшим количеством информации имеют большие ячейки (даже если это не так). Можно выбрать интерполяцию "линейно", тогда области с меньшим количеством информации выглядят менее резкими. Дело вкуса, правда.
points = np.array([x, y]).T # because griddata wants it that way
z_grid2 = griddata(points, z, grid, method='nearest')
# you get a 1D vector as result. Reshape to picture format!
z_grid2 = z_grid2.reshape(xx.shape[0], yy.shape[0])
И хоп, мы передаем Matplotlib для отображения сюжета
fig = plt.figure(1, figsize=(10, 10))
ax1 = fig.add_subplot(111)
ax1.imshow(z_grid2, extent=[x_min, x_max,y_min, y_max, ],
origin='lower', cmap=cm.magma)
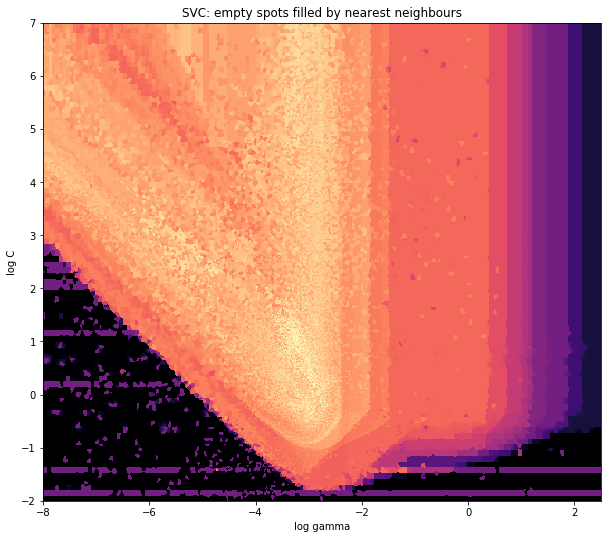
ax1.set_title("SVC: empty spots filled by nearest neighbours")
ax1.set_xlabel('log gamma')
ax1.set_ylabel('log C')
plt.show()
Вокруг заостренной части V-образной формы, как вы видите, я провел много вычислений во время поиска наилучшего места, в то время как менее интересные детали почти везде имеют более низкое разрешение.
Создайте 2-мерный массив, который соответствует ячейкам вашего конечного изображения, называемый скажем heatmap_cells и создать его как все нули.
Выберите два коэффициента масштабирования, которые определяют разницу между каждым элементом массива в реальных единицах, например, для каждого измерения. x_scale а также y_scale, Выберите их так, чтобы все ваши точки данных попадали в границы массива тепловых карт.
Для каждого необработанного x_value а также y_value:
heatmap_cells[floor(x_value/x_scale),floor(y_value/y_scale)]+=1
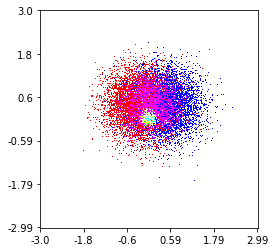
Вот один, который я сделал на наборе 1 миллион очков с 3 категориями (красный, зеленый и синий цвета). Вот ссылка на репозиторий, если вы хотите попробовать эту функцию. Github Repo
histplot(
X,
Y,
labels,
bins=2000,
range=((-3,3),(-3,3)),
normalize_each_label=True,
colors = [
[1,0,0],
[0,1,0],
[0,0,1]],
gain=50)
Очень похоже на ответ @Piti, но использует 1 вызов вместо 2 для генерации очков:
import numpy as np
import matplotlib.pyplot as plt
pts = 1000000
mean = [0.0, 0.0]
cov = [[1.0,0.0],[0.0,1.0]]
x,y = np.random.multivariate_normal(mean, cov, pts).T
plt.hist2d(x, y, bins=50, cmap=plt.cm.jet)
plt.show()
Выход:
Боюсь, я немного опоздал на вечеринку, но у меня был похожий вопрос некоторое время назад. Принятый ответ (@ptomato) помог мне, но я также хотел бы опубликовать его, если он кому-то пригодится.
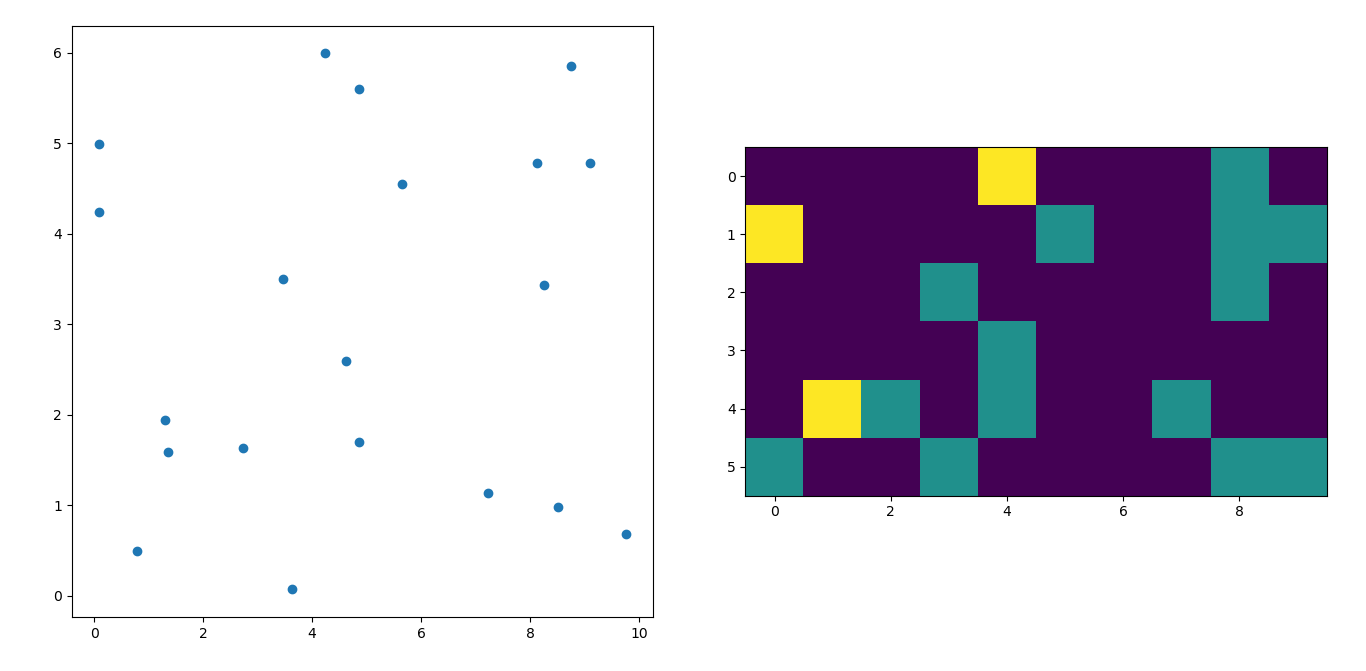
''' I wanted to create a heatmap resembling a football pitch which would show the different actions performed '''
import numpy as np
import matplotlib.pyplot as plt
import random
#fixing random state for reproducibility
np.random.seed(1234324)
fig = plt.figure(12)
ax1 = fig.add_subplot(121)
ax2 = fig.add_subplot(122)
#Ratio of the pitch with respect to UEFA standards
hmap= np.full((6, 10), 0)
#print(hmap)
xlist = np.random.uniform(low=0.0, high=100.0, size=(20))
ylist = np.random.uniform(low=0.0, high =100.0, size =(20))
#UEFA Pitch Standards are 105m x 68m
xlist = (xlist/100)*10.5
ylist = (ylist/100)*6.5
ax1.scatter(xlist,ylist)
#int of the co-ordinates to populate the array
xlist_int = xlist.astype (int)
ylist_int = ylist.astype (int)
#print(xlist_int, ylist_int)
for i, j in zip(xlist_int, ylist_int):
#this populates the array according to the x,y co-ordinate values it encounters
hmap[j][i]= hmap[j][i] + 1
#Reversing the rows is necessary
hmap = hmap[::-1]
#print(hmap)
im = ax2.imshow(hmap)
Ни одно из этих решений не сработало для моего приложения, поэтому я придумал это. По сути, я помещаю 2D Gaussian в каждую точку:
import cv2
import numpy as np
import matplotlib.pyplot as plt
def getGaussian2D(ksize, sigma, norm=True):
oneD = cv2.getGaussianKernel(ksize=ksize, sigma=sigma)
twoD = np.outer(oneD.T, oneD)
return twoD / np.sum(twoD) if norm else twoD
def pt2heat(pts, shape, kernel=16, sigma=5):
heat = np.zeros(shape)
k = getGaussian2D(kernel, sigma)
for y,x in pts:
x, y = int(x), int(y)
for i in range(-kernel//2, kernel//2):
for j in range(-kernel//2, kernel//2):
if 0 <= x+i < shape[0] and 0 <= y+j < shape[1]:
heat[x+i, y+j] = heat[x+i, y+j] + k[i+kernel//2, j+kernel//2]
return heat
heat = pts2heat(pts, img.shape[:2])
plt.imshow(heat, cmap='heat')
Вот точки, наложенные поверх связанного изображения, вместе с получившейся тепловой картой: