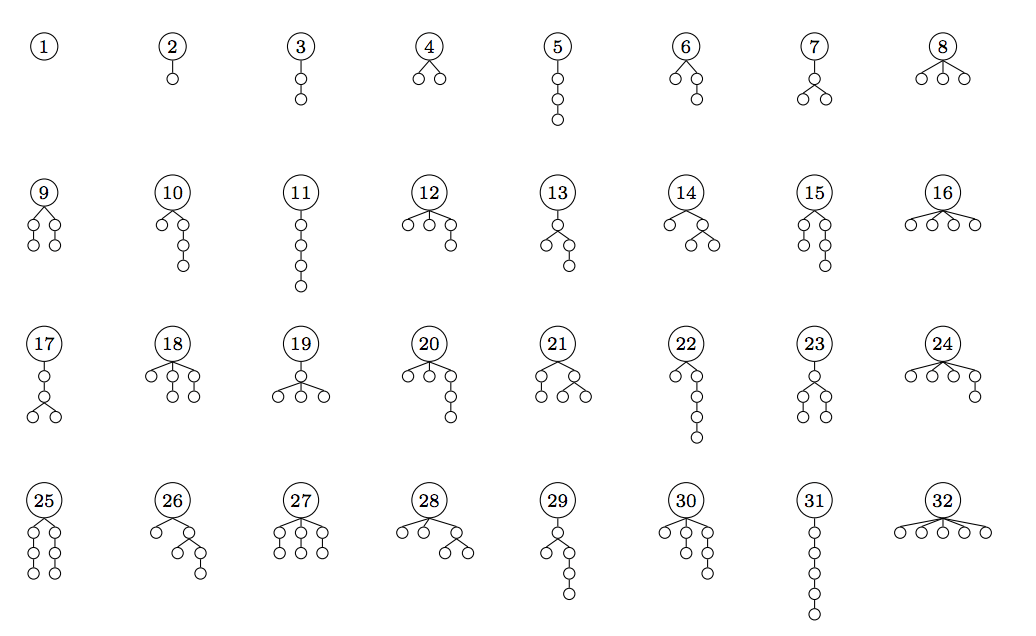Решение изоморфизма деревьев с помощью хеширования
Учитывая 2 дерева с известными корнями, как мы можем эффективно определить, являются ли деревья изоморфными? Мы заботимся только о форме дерева, а не о значениях узлов. Если одно дерево можно превратить в другое, переименовав его узлы, то деревья изоморфны. Алгоритм не обязательно должен быть правильным в 100% случаев, поэтому мы можем использовать хеширование, если коллизии хэшей встречаются редко.
Редактировать: найдено решение, удален ненужный беспорядок из этого поста
2 ответа
После большой работы и некоторой помощи, я пришел к решению O(n log n), которое также оказывается правильным в 100% случаев. Он основан на 2 идеях:
Идея 1: дерево может быть представлено в виде строки, в которой перечислены его поддеревья. Например, лист может быть представлен как "L". Дерево, которое имеет 2 листа, может быть представлено как "(L),(L)". Дерево, у которого есть поддерево, которое имеет 2 листа, может быть представлено как "((L),(L))" и т. Д. Проблема с этим подходом состоит в том, что большие деревья приводят к длинным, повторяющимся строкам, которые замедляют алгоритм вниз.
Идея 2: Строки могут быть проиндексированы в hashmap. Вместо того, чтобы переносить подстроку типа "((L),(L))", мы можем присвоить этой строке порядковый номер, скажем, 2. Теперь мы можем ссылаться на это поддерево и все идентичные поддеревья на "2", а не используя Строковое представление. Строки - это ключи в хэш-карте, а значения - это уникальные целые числа, назначенные этим строкам.
Вот код для построения hashmap из первого дерева:
Наш первый звонок должен быть fill(root, -1, 1)
public static int fill(int current, int previous, int height) {
ArrayList<Integer> subtrees = new ArrayList<>();
for (int next : edges[current]) {
if (next == previous) continue;
int subtree = fill(next, current, height+1);
subtrees.add(subtree);
}
// We have to sort subtrees for "2,4" and "4,2" to be considered the same
Collections.sort(subtrees);
StringBuilder sb = new StringBuilder(height + ".");
for (Integer subtree : subtrees) {
sb.append(subtree +",");
}
String key = new String(sb);
if (map.containsKey(key)) return map.get(key);
int index = map.size(); // assigning next available number
map.put(key, index);
return index;
}
Теперь мы можем вызвать fill для Tree 2 (заменить "ребра" информацией Tree 2, оставить HashMap без изменений). Если он возвращает одно и то же целое число, деревья совпадают.
Большая заслуга http://logic.pdmi.ras.ru/~smal/files/smal_jass08_slides.pdf
Вы также можете использовать дерево Дэвида Матула - целочисленная биекция, которая отображает деревья в целые числа.
Это метод для присвоения каждому дереву уникального натурального числа.
Вот примеры первых 32 деревьев:
Для ознакомления с алгоритмом см. Упражнения в этом документе: http://williamsharkey.com/integer-tree-isomorphism.pdf