Как рассчитать время рекурсивного вычисления n-го числа Фибоначчи?

Question

Как узнать, сколько времени требуется для вычисления n-го числа Фибоначчи на текущей машине? Например, на текущей машине 30-й элемент рассчитывается за 67 мс, а 40-й - за 554 мс. Как рассчитать время для 99-го элемента?

int fib(int n)
{
    if( n <= 2) 
        return 1
    else
        return fib(n-1) + fib(n-2)
}

---

ОБНОВИТЬ

Фибоначчи, Nth против мс (время, которое текущий компьютер вычисляет для вычисления n-го элемента Фибоначчи, время в мс) http://pastebin.com/PGnd54Hq

Matlab: код http://pastebin.com/L9CH53Pf

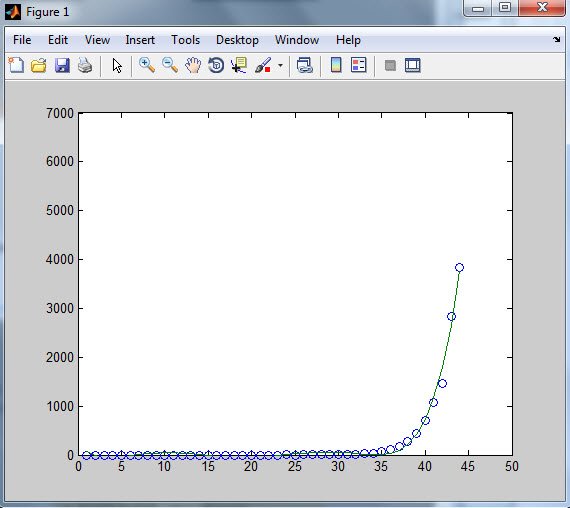
Как узнать время для N-го элемента?

Answer 1

Я бы измерил время для диапазона значений и составил бы таблицу:

n | time

а затем использовать matlab чтобы соответствовать экспоненциальной функции.

• Подогнать экспоненциальную кривую через точки данных в Matlab
• экспоненциальная форма, без стартером предугадывать
• Построение экспоненциальных кривых

имейте в виду, что нотация big-O асимптотична и справедлива для большого числа элементов.

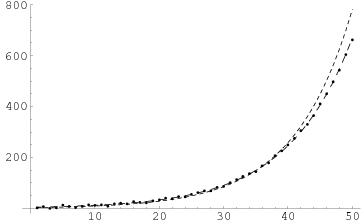
Вы должны попытаться написать код для него. используя встроенную функцию подпрограммы Фибоначчи, получите время использования ctime и сохраните значения в двух массивах. и после этого анализируя результаты с помощью matlab или `питон.

пожалуйста, опубликуйте свои результаты...

Answer 2

Легко доказать, что число рекурсивных вызовов функции также следует последовательности Фибоначчи. Как если бы F0=0 а также F1=1 ваши базовые случаи тогда F2 требуется 2 вызова функции и F3 понадобится 3 и так далее.

Это оправдывает использование экспоненциальной функции, чтобы соответствовать вашему времени, как предложено @0x90.

Answer 3

Видимо, вы запускаете реализацию наивного алгоритма для вычисления последовательности Фибоначчи. Этот алгоритм имеет экспоненциальную сложность: вычислительная сложность последовательности Фибоначчи (~ θ(1.6n)). Таким образом, время работы вашей программы на вашем компьютере будет примерно k*1.6n, Зная результат функции (время выполнения вашей программы) для одного n Вы должны быть в состоянии рассчитать константу k и, таким образом, рассчитать приблизительное время для разных n,

Answer 4

Производительность определяется не только количеством вызовов функций и количеством вычислений внутри каждого вызова, но и тем, что вы платите - по времени - за то, что все больше и больше стекаете в стек из-за рекурсивного алгоритма. Я не знаю, как происходит это стекание, но, вероятно, оно начинает расти быстрее после определенного порога. Итак, вам нужно выяснить, где этот порог срабатывает и подходит (экспоненциально или как-то еще) как ниже, так и выше (и, возможно, существуют более похожие ограничения производительности, когда вы начинаете создавать рекурсивный стек).

Очевидно - хотя это и не вопрос - числа Фибоначчи не должны вычисляться рекурсивным способом, даже если это математически элегантно и требует самого простого кода.

[ДОБАВЛЕНО / ИЗМЕНЕНО] Я заметил, что вы добавили график измерения времени. Чтобы лучше понять, я предлагаю использовать шкалу LOGARITHMIC по вертикали (раз). Это более четко покажет, является ли весь граф "чисто" экспоненциальным - прямая линия на логарифмическом графике - или это скорее последовательность (разных) экспонент или еще что-то еще. Возможно, экспоненциальная часть начинается "где-то" или превращается в другую экспоненциальную.

Answer 5

Из указанного кода каждый звонок совершает 2 звонка. Таким образом, простой ответ на этот вопрос заключается в том, что количество вызовов удваивается для каждого n, поэтому количество вызовов составляет 2^(n-1). Например, если вы вычисляете fib( 10), то количество вызовов будет 2^9 = 512. Таким образом, если для его создания понадобится 1 секунда, для всех вызовов fib (10) потребуется 512 секунд.).