Пытаетесь посчитать шаги через рекурсию?

Question

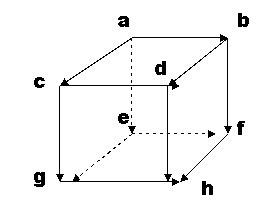
Это куб, края которого направлены; Он может идти только слева направо, сзади вперед и сверху вниз.

edge(a,b).
edge(a,c).
edge(a,e).
edge(b,d).
edge(b,f).
edge(c,d).
edge(c,g).
edge(d,h).
edge(e,f).
edge(e,g).
edge(f,h).
edge(g,h).

С помощью метода ниже мы можем проверить, можем ли мы перейти от AH, например: cango(A,H).

move(X,Y):- edge(X,Y).
move(X,Y):- edge(X,Z), move(Z,Y).

С move2 я пытаюсь подсчитать необходимые шаги.

move2(X,Y,N):- N is N+1, edge(X,Y).
move2(X,Y,N):- N is N+1, edge(X,Z), move2(Z,Y,N).

Как бы я это реализовал?

Answer 1

move2(X,Y,1):- edge(X,Y), ! .
move2(X,Y,NN):- edge(X,Z), move2(Z,Y,N), NN is N+1 .

Answer 2

Арифметическая оценка выполняется как обычно в Прологе, но назначение не работает как обычно. Затем вам нужно ввести новую переменную для увеличения значения:

move2(X,Y,N,T):- T is N+1, edge(X,Y).
move2(X,Y,N,T):- M is N+1, edge(X,Z), move2(Z,Y,M,T).

и инициализировать N к 0 при первом вызове. Такие добавленные переменные (в нашем случае T) часто называют аккумуляторами.

Answer 3

(is)/2 очень чувствителен к экземплярам в своем втором аргументе. Это означает, что вы не можете использовать его полностью реляционным образом. Вы можете спросить X is 1+1.можно даже спросить 2 is 1+1. но вы не можете спросить: 2 is X+1,

Поэтому, когда вы программируете с такими предикатами, как (is)/2Вы должны представить, с какими режимами будет использоваться предикат. Такие соображения легко приводят к ошибкам, в частности, если вы только начали. Но не волнуйтесь, более опытные программисты все еще становятся жертвами таких проблем.

Существует чистая альтернатива в нескольких системах Prolog: в SICStus, YAP, SWI есть library(clpfd) что позволяет вам выразить отношения между целыми числами. Обычно эта библиотека используется для программирования ограничений, но вы также можете использовать ее как безопасную и чистую замену (is)/2 на целых числах. Более того, эта библиотека часто очень эффективно компилируется, так что результирующий код сопоставим по скорости (is)/2,

?- use_module(библиотека (clpfd)).
правда.?- X #= 1+1.
Х = 2?- 2 #= 1+1.
правда.?- 2 #= X+1.
Х = 1

Теперь вернемся к вашей программе, вы можете просто написать:

move2 (X, Y, 1): - край (X,Y).
move2(X,Y,N0):- N0 #>= 1, N0 #= N1+1, ребро (X,Z), move2(Z,Y,N1).

Теперь вы получаете все расстояния по мере необходимости.

Но это еще не все...

Чтобы убедиться, что move2/3 фактически завершается, попробуйте:

? - move2 (A, B, N), false.
ложный.

Теперь мы можем быть уверены, что move2/3 всегда заканчивается Всегда? Предположим, вы добавили еще одно преимущество:

edge(f, f).

Теперь над циклами запросов. Но все же вы можете использовать вашу программу в ваших интересах! Определить количество узлов:

? - setof (C, A ^ B ^ (ребро (A,B), член (C,[A,B])),Cs), длина (Cs, N).
Cs = [a, b, c, d, e, f, g, h],
N = 8

Так что самый длинный путь займет всего 7 шагов!

Теперь вы можете задать запрос еще раз, но теперь, ограничив N до значения, меньшего или равного 7:

? - 7 #> = N, move2 (A, B, N), false.
ложный.

С этим дополнительным ограничением у вас снова есть завершающее определение! Нет больше петель.