ODE45 с очень большими числами в качестве ограничений

Question

2-^й ODE для решения в MATLAB:

  ( (a + f(t))·d²x/dt² + (b/2 + k(t))·dx/dt ) · dx/dt - g(t) = 0

Граничное условие:

 dx/dt(0) = v0

где

• t это время,
• x это позиция
• dx/dt это скорость
• d2x/dt2 это ускорение
• a, b, v0 являются постоянными
• f(t), k(t) а также h(t) ИЗВЕСТНЫЕ функции зависят от t(Я не пишу их, потому что они довольно большие)

В качестве примера, используя символические переменные:

syms t y
%% --- Initial conditions ---
   phi = 12.5e-3;
   v0 = 300;            
   e  = 3e-3;           
   ro = 1580;          
   E  = 43e9;   
   e_r = 0.01466;  
   B = 0.28e-3; 

%% --- Intermediate calculations ---
   v_T = sqrt(((1 + e_r) * 620e6) /E) - sqrt(E/ro) * e_r;
   R_T = v_T * t;                   
   m_acc = pi * e * ro *(R_T^2);  
   v_L = sqrt (E/ro);           
   R_L = v_L * t;    
   z = 2 * R_L;                   
   E_4 = B * ((e_r^2)* B * (0.9^(z/B)-1)) /(log(0.9));
   E_1 = E * e * pi * e_r^2 * (-phi* (phi - 2*v_T*t)) /16; 
   E_2 = pi * R_T^2 * 10e9;        
   E_3 = pi * R_T^2 * 1e6 * e;   

    %% Resolution of the problem  
        g_t = -diff(E_1 + E_2 + E_3, t); 

f(t,y)=(g_t - (pi*v_T*e*ro/2 + E_4) * y^2 /(y* (8.33e-3 + m_acc))];
fun=matlabFunction(f);
[T,Y]=ode45(fun,[0 1], v0]);

Как я могу переписать это, чтобы получить x как y=dx/dt? Я новичок в Matlab, и любая помощь очень приветствуется!

Answer 1

Во-первых, вы должны использовать subs оценить символическую функцию. Другой подход заключается в использовании matlabFunction для преобразования всех символических выражений в анонимные функции, как это было предложено Horchler.

Во-вторых, вы интегрируете ODE, как будто это 1- ^й порядок в dx/dt, Если вы заинтересованы в x(t) так же как dx/dt(t) тогда вам придется изменить функцию следующим образом:

fun = @(t,y) [y(2);   
             ( subs(g) - (b/2 + subs(k))*y(2)*y(2) ) / ( y(2) * (a + subs(f))) ];

и, конечно же, укажите начальное значение для x0 = x(0) так же как v0 = dx/dt(0),

В-третьих, абсолютное значение параметров вряд ли когда-либо вызывает серьезную озабоченность. Формат с плавающей точкой двойной точности IEEE754 может легко представлять числа между 2.225073858507201e-308 а также 1.797693134862316e+308 (realmin а также realmax соответственно). Таким образом, для коэффициентов, которые вы дали (O (10 ¹⁴)), это абсолютно не проблема. Вы можете потерять несколько цифр точности, если не будете принимать меры предосторожности (измените масштаб на [-1 +1] переформулируйте проблему в разных единицах, ...), но относительная ошибка из-за этого более чем вероятно будет крошечной и незначительной по сравнению с алгоритмической ошибкой, допущенной ode45,

<RANDOM_OPINIONATED_RANT>

В-четвертых, ПОЧЕМУ вы используете символическую математику для этой цели?! Вы делаете числовую интеграцию, то есть аналитическое решение в любом случае отсутствует. Зачем тогда заниматься символикой? Выполнение интеграции с символикой (через vpa даже) будет в десятки, сотни, да, зачастую даже в тысячи раз медленнее, чем сохранение (или повторная реализация) всего числового (что, как некоторые утверждают, в MATLAB уже медленное по сравнению с подходом "голый металл").

Да, конечно, для этого конкретного, индивидуального, изолированного варианта использования это может не иметь большого значения, но в будущем я настоятельно рекомендую вам научиться:

• использовать символику для дериваций, доказательство теорем, упрощение выражений,...
• используйте цифры для реализации любого алгоритма или функции, от которых ожидаются фактические числа.

Другими словами, символика для черчения, цифры для хруста. И точно нулевая символика должна появляться в любой хорошей реализации любого алгоритма.

Хотя их можно смешивать до некоторой степени, это не значит, что это хорошая идея. На самом деле, это почти никогда. И те немногие единичные случаи, когда это единственный жизнеспособный вариант, не являются подтверждением этого подхода. Они редкие, в конце концов единичные случаи, далекие от обильной нормы.

Для меня это имеет сходство со злом eval с аналогичными причинами, почему это должно. Быть. Избегать

</RANDOM_OPINIONATED_RANT>

Answer 2

С полным кодом легко найти полное решение:

% Initial conditions
phi = 12.5e-3;
v0  = 300;
x0  = 0;    % (my assumption)
e   = 3e-3;
ro  = 1580;
E   = 43e9;
e_r = 0.01466;
B   = 0.28e-3;

% Intermediate calculations
v_T = sqrt(((1 + e_r) * 620e6) /E) - sqrt(E/ro) * e_r;
R_T = @(t) v_T * t;
m_acc = @(t) pi * e * ro *(R_T(t)^2);
v_L = sqrt (E/ro);
R_L = @(t) v_L * t;
z   = @(t) 2 * R_L(t);
E_4 = @(t) B * ((e_r^2)* B * (0.9^(z(t)/B)-1)) /(log(0.9));

% UNUSED
%{
E_1 = @(t) -phi * E * e * pi * e_r^2 * (phi - 2*v_T*t) /16;
E_2 = @(t) pi * R_T(t)^2 * 10e9;
E_3 = @(t) pi * R_T(t)^2 * 1e6 * e;
%}

% Resolution of the problem
g_t = @(t)  -( phi * E * e * pi * e_r^2 * v_T / 8 + ...  % dE_1/dt
               pi * 10e9 * 2 * R_T(t) * v_T + ...        % dE_2/dt
               pi * 1e6 * e * 2 * R_T(t) * v_T );        % dE_3/dt

% The derivative of Z = [x(t); x'(t)] equals Z' = [x'(t);  x''(t)]
f = @(t,y)[y(2);
          (g_t(t) - (0.5*pi*v_T*e*ro + E_4(t)) * y(2)^2) /(y(2) * (8.33e-3 + m_acc(t)))];

% Which is readily integrated
[T,Y] = ode45(f, [0 1], [x0 v0]);

% Plot solutions
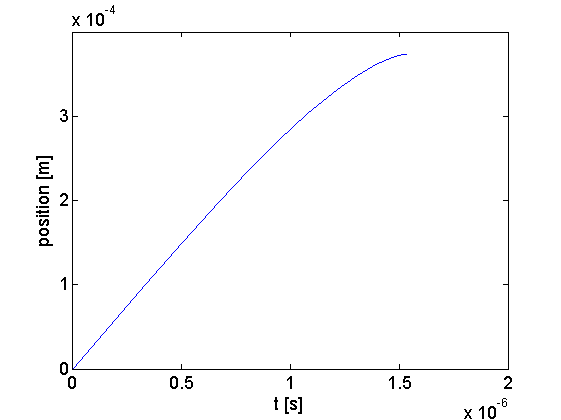
figure(1)
plot(T, Y(:,1)) 
xlabel('t [s]'), ylabel('position [m]')

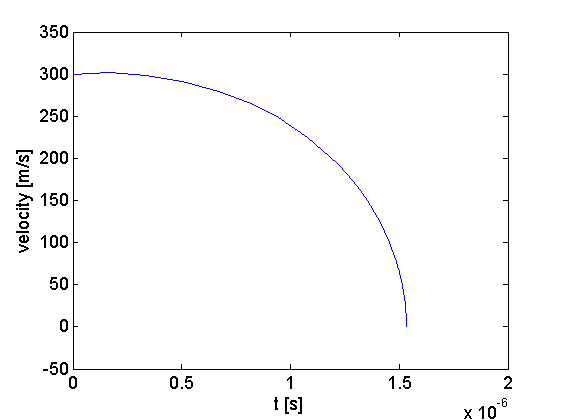
figure(2)
plot(T, Y(:,2)) 
xlabel('t [s]'), ylabel('velocity [m/s]')

Результаты:

Обратите внимание, что я нигде не использовал символику, кроме как для двойной проверки моих производных от руки.