Корректность минимального количества свопов для сортировки массива

Question

Вопрос от здесь: https://www.geeksforgeeks.org/minimum-number-swaps-required-sort-array/

Я повторю это ниже: учитывая массив из n различных элементов, найдите минимальное количество перестановок, необходимое для сортировки массива.

Примеры:

Входные данные: {4, 3, 2, 1} Выходные данные: 2 Объяснение: Поменяйте местами индекс 0 на 3 и 1 на 2, чтобы сформировать отсортированный массив {1, 2, 3, 4}.

Вход: {1, 5, 4, 3, 2} Выход: 2

Я решил проблему, выполнив следующее.

1. Сортировка массива (n log(n)) по времени
2. Создание хэша для отслеживания необходимых перестановок, поскольку я сравниваю отсортированный массив и исходный массив. Это должно быть другое время O(n)

Общая сложность времени должна быть: O(n + (n log n)) = O(n log(n))

Ниже приведен код, который я написал для того же, и он работает для предоставленных тестовых случаев.

def solution(array)

  sorted = array.sort
  puts array.inspect
  puts sorted.inspect

  counter_parts_that_have_been_seen = {}

  number_of_swaps_required = 0

  array.each_with_index do | val, idx |
    if counter_parts_that_have_been_seen[val] == true
      next
    end

    array_val = val
    sorted_val = sorted[idx]

    if array_val != sorted_val
      puts "A swap will be required: array val is #{array_val} and sorted_array_val is #{sorted_val}"
      number_of_swaps_required += 1
      counter_parts_that_have_been_seen[sorted_val] = true
    end
  end

  puts "Number of swaps required are: #{number_of_swaps_required}"

end

Теперь мой вопрос: как проверить правильность? У меня нет ощущения погоды, такой подход правильный.

Кто-нибудь может пролить свет на это?

Answer 1

Если есть элемент, который находится не в правильном положении, то должен быть также другой элемент, который также находится в неправильном положении (первый элемент необходимо поместить в какую-то другую позицию, которая занята другим элементом). Если это представлено в виде графика, позиции, в которых нет правильных элементов, будут иметь одно ребро по направлению к нему и край от него. В итоге получится один или несколько циклов. Теперь все позиции элементов в цикле находятся внутри этого цикла. Итак, теперь нам нужно доказать, что если в цикле есть n элементов, для их сортировки требуется минимум n-1 свопов. Мы можем доказать, что это индукция.

База: n = 1
Только один элемент, поэтому уже отсортирован (тривиально). Это означает 0 свопов, т. Е. N-1 => 1-1 = 0

Предположим, что если в цикле k элементов, требуется минимум k-1 перестановок

k + 1 элементов
У элемента в цикле есть край в направлении позиции, в которой он должен быть. У этой позиции есть еще одно преимущество по отношению к какой-то другой позиции. Теперь, если мы поменяем местами первый элемент, мы удалим первый край, а последний элемент перейдет в замененное положение. Теперь у нас остался цикл размера (k+1)-1 = k. По индукции, k-цикл требует k-1 перестановок. Итак, k+1 потребует (k-1)+1 = k свопов.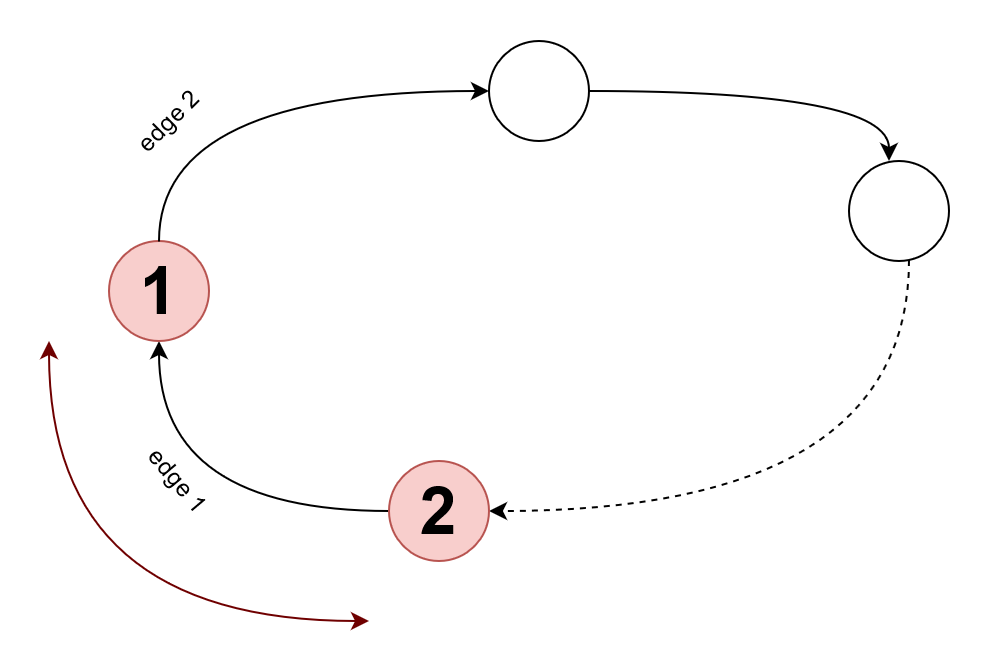

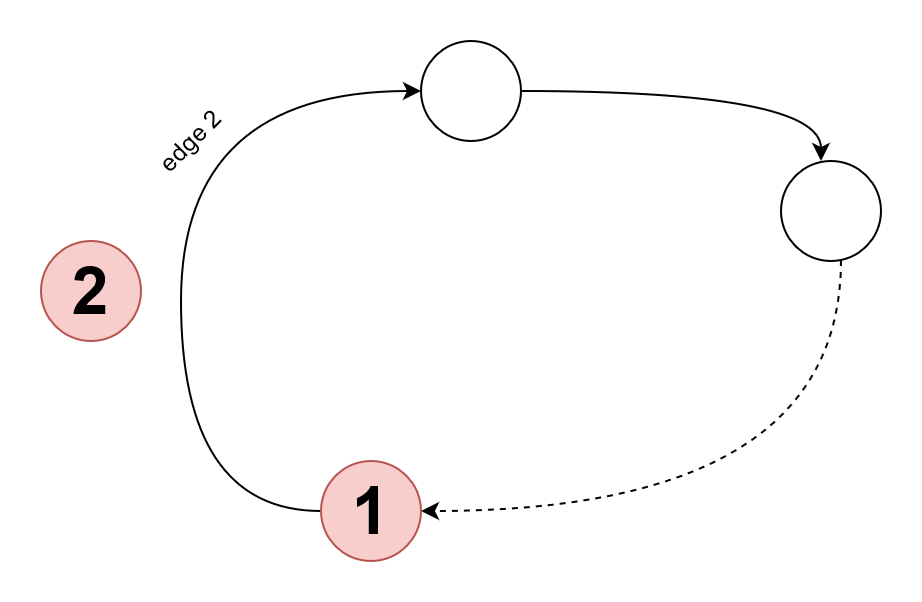
Answer 2

Начиная с первого элемента в несортированном массиве, проверьте, находится ли он в правильном месте, если не поменяйте местами правильное значение в эту позицию. Тест можно выполнить, как вы, сравнив отсортированную версию коллекции, или выбранный элемент можно сравнить с каждым последующим элементом.

По мере продвижения вы можете столкнуться с элементами, которые находятся в правильном положении - либо потому, что они начались в правильном месте, либо они были поменяны местами при размещении более раннего элемента (последний элемент должен быть к тому времени, когда все остальные были размещены). Просто оставьте их на месте и переходите к следующему элементу.

При этом методе каждый своп размещает хотя бы один элемент правильно, некоторые свопы правильно размещают оба.

Элемент в правильном месте может быть исключен из проблемы - никогда не нужно перемещать его из правильного места для сортировки любых других элементов. Также пару элементов, которые в других местах (например, 3 и 1 в {3,2,1}), никогда не нужно менять местами ни с одним из других элементов. Они формируют свой собственный независимый набор элементов.

Если у вас есть метод, как описано выше, для получения правильного ответа, его, очевидно, можно использовать для оценки любого альтернативного метода.

Answer 3

Index :   0   1   2   3   4   5   6   7   8   9
------+-----+---+---+---+---+---+---+---+---+--
Array :   1  22  32  42  12  83  64  93  73  53
------+-----+---+---+---+---+---+---+---+---+--
          A  BBBBBBBBBBBBBB  CC  DD  CCCCCCCCCC
Target:   0   2   3   4   1   8   6   9   7   5
Diffs :   0   1   1   1  -3   3   0   2  -1  -4
Source:   0   4   1   2   3   9   6   8   5   7

В этом примере массив [] должен быть отсортирован.

• Target - это индекс, по которому эта позиция должна идти после сортировки.
• источником является позиция, где этот индекс должен получить свое значение из
• diffs - относительное движение, которое элемент с этим индексом делает во время сортировки

Вы можете увидеть четыре (циклические) группы:

• A: 1 участник 1
• B: 4 члена {22,32,42,12}
• C: 4 члена: {83,93,73,53}
• D: 1 участник: 64

Группы с 1 участником уже отсортированы: требуется замена нуля. Группы с 4 участниками могут быть отсортированы с 4 перестановками в каждой. (последний своп помещает два элемента в их окончательное место) Таким образом, необходимое количество свопов составляет 0+3+3+0

Теперь вам нужно только доказать, что вы можете отсортировать N-цикл в обменах N-1...