Арифметика одинарной точности нарушается при выполнении скомпилированного кода x86 на 64-битной машине

Question

Когда вы читаете MSDN наSystem.Single:

Single соответствует стандарту IEC 60559:1989 (IEEE 754) для двоичной арифметики с плавающей точкой.

и спецификация языка C#:

float а также double типы представлены с использованием 32-разрядных форматов IEEE 754 с одинарной точностью и 64-разрядных с двойной точностью [...]

и позже:

Произведение рассчитывается в соответствии с правилами арифметики IEEE 754.

у вас легко складывается впечатление, что float тип и его умножение соответствуют IEEE 754.

Это часть IEEE 754, что умножение четко определено. Я имею в виду, что когда у вас есть два float экземпляры, существует один и только один float который является их "правильным" продуктом. Не допускается, чтобы продукт зависел от некоторого "состояния" или "настройки" системы, которая его вычисляет.

Теперь рассмотрим следующую простую программу:

using System;

static class Program
{
  static void Main()
  {
    Console.WriteLine("Environment");
    Console.WriteLine(Environment.Is64BitOperatingSystem);
    Console.WriteLine(Environment.Is64BitProcess);
    bool isDebug = false;
#if DEBUG
    isDebug = true;
#endif
    Console.WriteLine(isDebug);
    Console.WriteLine();

    float a, b, product, whole;

    Console.WriteLine("case .58");
    a = 0.58f;
    b = 100f;
    product = a * b;
    whole = 58f;
    Console.WriteLine(whole == product);
    Console.WriteLine((a * b) == product);
    Console.WriteLine((float)(a * b) == product);
    Console.WriteLine((int)(a * b));
  }
}

Начните с написания некоторой информации об окружающей среде и скомпилируйте конфигурацию, программа просто считает два floatс (а именно a а также b) и их продукт. Последние четыре строки записи являются интересными. Вот результат выполнения этого на 64-битной машине после компиляции с Debug x86 (слева), Release x86 (в середине) и x64 (справа):

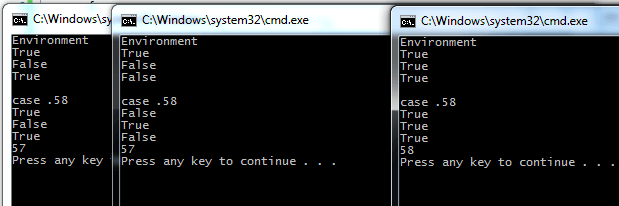
Мы заключаем, что результат простого float Операции зависят от конфигурации сборки.

Первая строка после "case .58" это простая проверка равенства двух floats. Мы ожидаем, что он не зависит от режима сборки, но это не так. Следующие две строки мы ожидаем, чтобы быть идентичными, потому что это ничего не меняет, чтобы бросить float к float, Но это не так. Мы также ожидаем, что они прочитают "True↩ True" потому что мы сравниваем продукт a*b к себе. Последняя строка вывода, которую мы ожидаем, не зависит от конфигурации сборки, но это не так.

Чтобы выяснить, что является правильным продуктом, мы рассчитываем вручную. Бинарное представление 0.58 (a) является:

0 . 1(001 0100 0111 1010 1110 0)(001 0100 0111 1010 1110 0)...

где блок в скобках - это период, который повторяется вечно. Представление с одинарной точностью для этого числа должно быть округлено до:

0 . 1(001 0100 0111 1010 1110 0)(001      (*)

где мы округлились (в данном случае округлились вниз) до ближайшего представимого Single, Теперь число "сто" (b) является:

110 0100 .       (**)

в двоичном Вычисление полного произведения чисел (*) а также (**) дает:

 11 1001 . 1111 1111 1111 1111 1110 0100

который округляется (в данном случае округляется) до одинарной точности, дает

 11 1010 . 0000 0000 0000 0000 00

где мы собрались, потому что следующий бит был 1не 0 (круглый до ближайшего). Итак, мы заключаем, что результат 58f в соответствии с IEEE. Это никоим образом не было дано априори, например 0.59f * 100f меньше чем 59f, а также 0.60f * 100f больше, чем 60fсогласно IEEE.

Таким образом, похоже, что x64-версия кода правильно поняла (крайнее правое окно вывода на картинке выше).

Примечание. Если у кого-либо из читателей этого вопроса установлен старый 32-разрядный процессор, было бы интересно услышать, что выводит вышеприведенная программа в своей архитектуре.

А теперь по вопросу:

1. Это ошибка?
2. Если это не ошибка, где в спецификации C# говорится, что среда выполнения может выбрать выполнение float умножение с дополнительной точностью, а затем "забыть" снова избавиться от этой точности?
3. Как можно кастинг float выражение для типа float изменить что-нибудь?
4. Разве не проблема в том, что, казалось бы, невинные операции, такие как разбиение выражения на два выражения, например, вытаскивая (a*b) к временной локальной переменной изменяет поведение, когда они должны быть математически (согласно IEEE) эквивалентны? Как программист может знать заранее, если среда выполнения решает удерживать float с "искусственной" дополнительной (64-битной) точностью или нет?
5. Почему "оптимизации" от компиляции в режиме Release позволяют изменять арифметику?

(Это было сделано в версии 4.0.NET Framework.)

Answer 1

Я не проверял вашу арифметику, но я наверняка видел подобные результаты раньше. Помимо того, что режим отладки имеет значение, назначение локальной переменной вместо переменной экземпляра также может иметь значение. Это допустимо в соответствии с разделом 4.1.6 спецификации C# 4:

Операции с плавающей запятой могут выполняться с большей точностью, чем тип результата операции. Например, некоторые аппаратные архитектуры поддерживают "расширенный" или "длинный двойной" тип с плавающей запятой с большей дальностью и точностью, чем double тип и неявно выполнять все операции с плавающей запятой, используя этот тип с более высокой точностью. Такие аппаратные архитектуры могут быть сделаны только при чрезмерных затратах на производительность для выполнения операций с плавающей запятой с меньшей точностью. Вместо того, чтобы требовать реализации для потери производительности и точности, C# позволяет использовать тип с более высокой точностью для всех операций с плавающей запятой. Помимо предоставления более точных результатов, это редко дает ощутимые результаты. [...]

Я не могу точно сказать, что здесь происходит, но я не удивлюсь.