Оптимальная 9-элементная сеть сортировки, которая сводится к оптимальной сети с медианой 9?
Я изучаю сети сортировки и медианного выбора для девяти элементов, основанные исключительно на операциях с двумя входами минимума / максимума. Кнут, TAOCP Vol. 3, 2-е изд. утверждает (стр. 226), что для сортировочной сети из девяти элементов требуется не менее 25 сравнений, что означает равное количество SWAP() примитивы или 50 мин / макс операций. Очевидно, что сортировочная сеть может быть преобразована в сеть с медианным выбором, исключая избыточные операции. Общепринятое мнение состоит в том, что это не приводит к оптимальной сети медианного отбора. Хотя это выглядит эмпирически верно, я не могу найти доказательств в литературе, что это обязательно так.
Лукаш Секанина, "Эволюционный проект освоения космоса для срединных цепей". В: EvoWorkshops, март 2004 г., стр. 240-249, минимальное количество минимальных / максимальных операций, необходимых для оптимальной сети медианного выбора из девяти входов, равно 30 (таблица 1). Я убедился, что это достигается как хорошо известной сетью медианного выбора, которую дал Джон Л. Смит, "Реализация медианных фильтров в FPGA XC4000E". Журнал XCELL, Vol. 23, 1996, с. 16, и сеть с медианой-9 из более ранней работы Чайтали Чакрабарти и Ли-Ю Вана "Новая сетевая архитектура сортировки для фильтров ранговых порядков". Транзакции IEEE для систем интеграции очень большого масштаба, Vol. 2, № 4 (1994), с. 502-507, где последний превращается в первый путем простого устранения избыточных компонентов. Смотрите варианты 4 и 5 в коде ниже.
Изучение опубликованных оптимальных сетей сортировки из девяти элементов на предмет их пригодности для преобразования в эффективные сети с медианным отбором путем исключения избыточных операций, лучшая версия, которую мне удалось найти, - это онлайн-генератор Джона М. Гэмбла, который требует 32 мин / макс операций, поэтому просто два стесняются оптимального количества операций. Это показано как вариант 1 в коде ниже. Другие оптимальные сети сортировки сокращают до 36 мин / макс операций (вариант 2) и 38 мин / макс операций (вариант 3) соответственно.
Существует ли какая-либо известная сеть сортировки из девяти элементов (т. Е. С 50 минимальными / максимальными операциями с двумя входами), которая сводится к оптимальной сети с медианой выбора из девяти входов (с 30 минимальными / максимальными операциями с двумя входами) за счет исключения только избыточных операций?
Код ниже использует float данные в качестве контрольного примера, поскольку многие процессоры предлагают операции с минимальным / максимальным значением для данных с плавающей запятой, но не для целочисленных данных, за исключением графических процессоров. Из-за проблем со специальными операндами с плавающей точкой (которые не встречаются в моем реальном случае использования), оптимальные последовательности кода обычно требуют использования режимов "быстрой математики", предлагаемых компиляторами, таких как в этом испытательном стенде Godbolt.
#include <cstdlib>
#include <cstdio>
#include <algorithm>
#define VARIANT 1
#define FULL_SORT 0
typedef float T;
#define MIN(a,b) std::min(a,b)
#define MAX(a,b) std::max(a,b)
#define SWAP(i,j) do { T s = MIN(a##i,a##j); T t = MAX(a##i,a##j); a##i = s; a##j = t; } while (0)
#define MIN3(x,y,z) MIN(a##x,MIN(a##y,a##z))
#define MAX3(x,y,z) MAX(a##x,MAX(a##y,a##z))
#define MED3(x,y,z) MIN(MAX(MIN(a##y,a##z),a##x),MAX(a##y,a##z))
#define SORT3(x,y,z) do { T s = MIN3(x,y,z); T t = MED3(x,y,z); T u = MAX3(x,y,z); a##x=s; a##y=t; a##z=u; } while (0)
/* Use sorting/median network to fully or partially sort array of nine values
and return the median value
*/
T network9 (T *a)
{
// copy to scalars
T a0, a1, a2, a3, a4, a5, a6, a7, a8;
a0=a[0];a1=a[1];a2=a[2];a3=a[3];a4=a[4];a5=a[5];a6=a[6];a7=a[7];a8=a[8];
#if VARIANT == 1
// Full sort. http://pages.ripco.net/~jgamble/nw.html
SWAP (0, 1); SWAP (3, 4); SWAP (6, 7); SWAP (1, 2); SWAP (4, 5);
SWAP (7, 8); SWAP (0, 1); SWAP (3, 4); SWAP (6, 7); SWAP (0, 3);
SWAP (3, 6); SWAP (0, 3); SWAP (1, 4); SWAP (4, 7); SWAP (1, 4);
SWAP (2, 5); SWAP (5, 8); SWAP (2, 5); SWAP (1, 3); SWAP (5, 7);
SWAP (2, 6); SWAP (4, 6); SWAP (2, 4); SWAP (2, 3); SWAP (5, 6);
#elif VARIANT == 2
// Full sort. Donald E. Knuth, TAOCP Vol. 3, 2nd ed., Fig 51
SWAP (0, 1); SWAP (3, 4); SWAP (6, 7); SWAP (1, 2); SWAP (4, 5);
SWAP (7, 8); SWAP (0, 1); SWAP (3, 4); SWAP (6, 7); SWAP (2, 5);
SWAP (0, 3); SWAP (5, 8); SWAP (1, 4); SWAP (2, 5); SWAP (3, 6);
SWAP (4, 7); SWAP (0, 3); SWAP (5, 7); SWAP (1, 4); SWAP (2, 6);
SWAP (1, 3); SWAP (2, 4); SWAP (5, 6); SWAP (2, 3); SWAP (4, 5);
#elif VARIANT == 3
// Full sort. Vinod K Valsalam and Risto Miikkulainen, "Using Symmetry
// and Evolutionary Search to Minimize Sorting Networks". Journal of
// Machine Learning Research 14 (2013) 303-331
SWAP (2, 6); SWAP (0, 5); SWAP (1, 4); SWAP (7, 8); SWAP (0, 7);
SWAP (1, 2); SWAP (3, 5); SWAP (4, 6); SWAP (5, 8); SWAP (1, 3);
SWAP (6, 8); SWAP (0, 1); SWAP (4, 5); SWAP (2, 7); SWAP (3, 7);
SWAP (3, 4); SWAP (5, 6); SWAP (1, 2); SWAP (1, 3); SWAP (6, 7);
SWAP (4, 5); SWAP (2, 4); SWAP (5, 6); SWAP (2, 3); SWAP (4, 5);
#elif VARIANT == 4
// Chaitali Chakrabarti and Li-Yu Wang, "Novel sorting network-based
// architectures for rank order filters." IEEE Transactions on Very
// Large Scale Integration Systems, Vol. 2, No. 4 (1994), pp. 502-507
// sort columns
SORT3 (0, 1, 2);
SORT3 (3, 4, 5);
SORT3 (6, 7, 8);
// sort rows
SORT3 (0, 3, 6); // degenerate: MAX3 -> a6
SORT3 (1, 4, 7); // degenerate: MED3 -> a4
SORT3 (2, 5, 8); // degenerate: MIN3 -> a2
// median computation
SORT3 (2, 4, 6); // degenerate: MED3 -> a4 has rank 4
#elif VARIANT == 5
// John L. Smith, "Implementing median filters in XC4000E FPGAs",
// XCELL magazine, Vol. 23, 1996, p. 16
SORT3 (0, 1, 2);
SORT3 (3, 4, 5);
SORT3 (6, 7, 8);
a3 = MAX3 (0, 3, 6); // a3 has rank 2,3,4,5,6
a4 = MED3 (1, 4, 7); // a4 has rank 3,4,5
a5 = MIN3 (2, 5, 8); // a5 has rank 2,3,4,5,6
a4 = MED3 (3, 4, 5); // a4 has rank 4
#else
#error unknown VARIANT
#endif
#if FULL_SORT
// copy back sorted results
a[0]=a0;a[1]=a1;a[2]=a2;a[3]=a3;a[4]=a4;a[5]=a5;a[6]=a6;a[7]=a7;a[8]=a8;
#endif
// return median-of-9
return a4;
}
1 ответ
Я не уверен, что это будет соответствовать всем критериям для того, что вы ищете, но вот способ превратить вариант 5 в 25-минутную / макс. Сортировочную сеть с 25-кратным обменом, а затем уменьшить ее до 30-минутной. / макс медиана выбора сети:
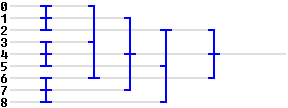
Мы начнем с сети медианного отбора (John L. Smith, 1996), в которой используются три SORT3, один MAX3, один MIN3 и два MED3:
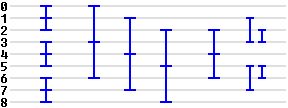
Мы изменили все MAX3, MIN3 и MED3 на SORT3 и добавили четыре SWAP, чтобы получить полную сеть сортировки:
(Нам не нужна полная сортировка троек 1,2,3 и 5,6,7 в конце, потому что 2 не может быть меньше, чем 1 и 3, а 6 не может быть больше, чем 5 и 7.)
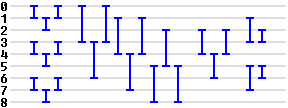
Когда мы заменяем SORT3 на SWAP, мы получаем стандартную сеть сортировки с 25 заменами:
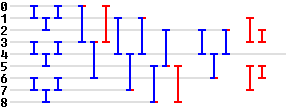
Затем мы можем уменьшить его до этой 30-минутной / максимальной сети среднего выбора:
MIN = Math.min; MAX = Math.max;
function sortingNetwork9(a) { // 50x min/max
swap(0,1); swap(3,4); swap(6,7);
swap(1,2); swap(4,5); swap(7,8);
swap(0,1); swap(3,4); swap(6,7);
swap(0,3); swap(3,6); swap(0,3);
swap(1,4); swap(4,7); swap(1,4);
swap(5,8); swap(2,5); swap(5,8);
swap(2,4); swap(4,6); swap(2,4);
swap(1,3); swap(2,3);
swap(5,7); swap(5,6);
function swap(i,j) {var tmp = MIN(a[i],a[j]); a[j] = MAX(a[i],a[j]); a[i] = tmp;}
}
function medianSelection9(a) { // 30x min/max
swap(0,1); swap(3,4); swap(6,7);
swap(1,2); swap(4,5); swap(7,8);
swap(0,1); swap(3,4); swap(6,7);
max(0,3); max(3,6); // (0,3);
swap(1,4); min(4,7); max(1,4);
min(5,8); min(2,5); // (5,8);
swap(2,4); min(4,6); max(2,4);
// (1,3); // (2,3);
// (5,7); // (5,6);
function swap(i,j) {var tmp = MIN(a[i],a[j]); a[j] = MAX(a[i],a[j]); a[i] = tmp;}
function min(i,j) {a[i] = MIN(a[i],a[j]);}
function max(i,j) {a[j] = MAX(a[i],a[j]);}
}
var a = [5,7,1,8,2,3,6,4,0], b = [5,7,1,8,2,3,6,4,0];
sortingNetwork9(a);
medianSelection9(b);
document.write("sorted: " + a + "<br>median: " + b[4]);