Как получить координаты пограничных точек встречи от scipy.spatial.Voronoi

Question

Я использую scipy.spatial.Voronoi для расчета диаграммы Вороного:

import numpy as np
from scipy.spatial import Voronoi

points = np.array([[51.129378, 17.02925 ],
                   [51.086225, 17.012689],
                   [50.913433, 15.765608],
                   [53.121764, 17.987906],
                   [53.134083, 17.995708],
                   [51.75805 , 19.529786]])


vor = Voronoi(points)

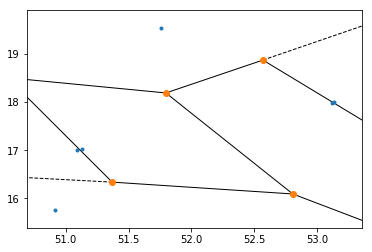
Я получаю следующую диаграмму формы:

Как получить координаты оранжевых точек? Кажется, что для него нет (по крайней мере документированного) атрибута.

Мотивация: Моя цель - рассчитать самый большой круг без синих точек. Поэтому я планирую рассчитать расстояния между каждой оранжевой и синей точками. Затем я проверю каждую оранжевую точку и выберу ту, которая будет иметь наибольшее минимальное значение расстояния. Это будет центр моего целевого круга. Может быть, есть другой способ сделать это без Вороного?

Answer 1

Эти пункты доступны в vertices приписывать. Документация Вороного описывает vertices атрибут "Координаты вершин Вороного". (Прокрутите вниз на связанной веб-странице, чтобы найти описания атрибутов.)

Вот ваш пример:

In [5]: import numpy as np

In [6]: from scipy.spatial import Voronoi

In [7]: points = np.array([[51.129378, 17.02925 ],
   ...:                    [51.086225, 17.012689],
   ...:                    [50.913433, 15.765608],
   ...:                    [53.121764, 17.987906],
   ...:                    [53.134083, 17.995708],
   ...:                    [51.75805 , 19.529786]])
   ...:                    

In [8]: vor = Voronoi(points)

Это точки, которые изображены в виде оранжевых точек:

In [9]: vor.vertices
Out[9]: 
array([[52.56952748, 18.87348869],
       [51.7974129 , 18.19059283],
       [56.91850562, 12.00665177],
       [52.80703622, 16.09228084],
       [50.53735155, 18.50739102],
       [51.36995954, 16.33786426]])

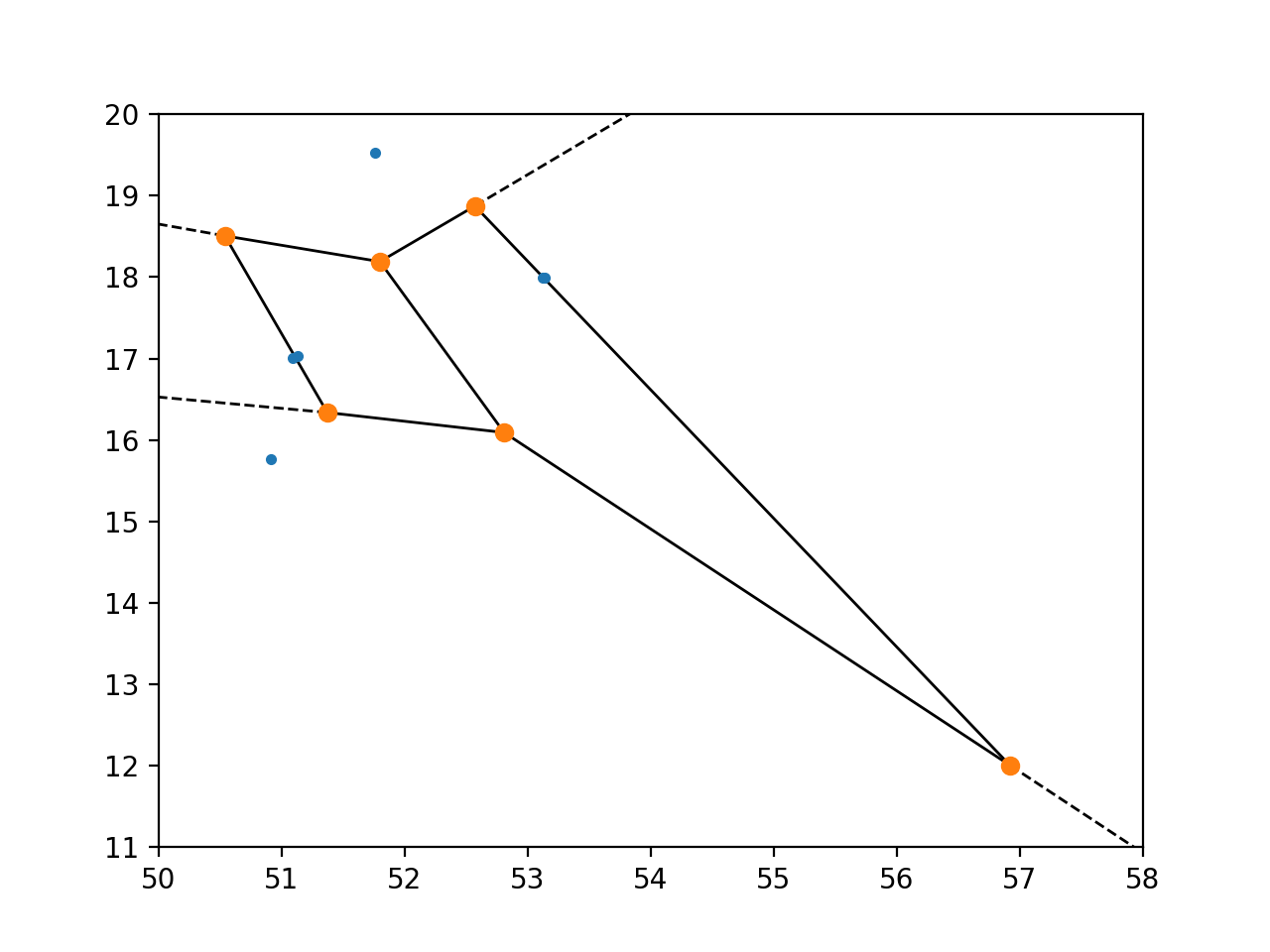
Обратите внимание, что voronoi_plot_2d(vor) выбирает x и y пределы на графике, которые слишком малы, чтобы видеть все вершины. Вот сюжет, который показывает их все:

In [15]: import matplotlib.pyplot as plt

In [16]: from scipy.spatial import voronoi_plot_2d

In [17]: voronoi_plot_2d(vor)
Out[17]: <Figure size 1280x960 with 1 Axes>

In [18]: plt.xlim(50, 58)
Out[18]: (50, 58)

In [19]: plt.ylim(11, 20)
Out[19]: (11, 20)