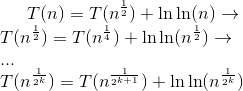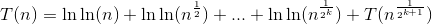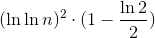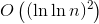Решить повторение: T(n) = T(n^(1/2)) + Θ(lg lg n)

Question

Начал изучение алгоритмов. Я понимаю, как найти тэта-нотацию из "регулярного повторения", такого как T(n) = Tf(n) + g(n), Но я потерян с этим повторением: проблема 1-2e:

T (n) = T (√n) + Θ (lg lg n)

Как выбрать метод для поиска тета? И что это за повторение? Я просто не совсем понимаю, что такое нотация внутри рекуррентности.

Answer 1

Один из трюков, который может быть полезен, состоит в том, чтобы преобразовать n во что-то другое, например, в 2^k. Если мы сделаем это, вы можете переписать вышесказанное как

T (2^k) = T (2^{k / 2}) + Θ (log log 2^k)

= T (2^k) = T (2^{k / 2}) + Θ (log k)

Теперь это похоже на повторение, которое мы могли бы реально решить, так как мы можем расширить это как

T (2^k) = T (2^{k / 2}) + log k = T (2^{k / 4}) + log (k / 2) + log k

Если мы расширим это раз, мы получим

T (2ⁱ) = T (2^{k / 2i}) + log k + log (k / 2) + log (k / 4) +... + log (k / 2ⁱ)

Это повторение заканчивается, когда 2^{k / 2i} ≤ 2 (скажем, в этом случае мы достигаем базового случая), что происходит, когда

2^{k / 2i} = 2

k / 2ⁱ = 1

k = 2^я

я = LG K

Другими словами, если мы можем написать n = 2^k, то чистый результат будет

T(n) = lg k + lg (k/2) + log (k/4) + log(k/8) + ... 1

LG K + (LG K) - 1 + (LG K) - 2 + (LG K) - 3 + ... + (LG K) - LG K

= Θ((LG K)²)

И так как мы знаем, что n = 2^k, это означает, что k = Θ(log n), поэтому, подставляя это в, мы получаем, что T (n) = Θ((log log n)²).

Основным трюком здесь было переписать n как 2^k. Остальное - стандартная техника.

Так имеет ли это смысл? Что ж, если вы подумаете об этом, log log n - это, среди прочего, количество бит, необходимое для записи log n. На каждой итерации вы берете квадратный корень из числа, что вдвое уменьшает количество бит в его представлении. Это уменьшает количество битов, необходимых для записи количества битов, в единицу. Следовательно, первая итерация будет записывать log log n битов, вторая (log log n) - 1, третья (log log n) - 2 и т. Д. В целом, это суммирование равно Θ ((log log n)²), что соответствует интуиции.

Надеюсь это поможет!

Answer 2

Вот как решить это с помощью математики. Я буду использовать lnln(n) вместо O(lnln(n)), Это в основном для уменьшения длины формул, и вы можете сделать то же самое с big-O. Так:

Который означает, что:

,

Теперь, чтобы преобразовать это большое суммирование, что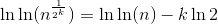

Целый lnln(n) сумма может быть преобразована как:

И наша единственная проблема - найти какую-то связь между n а также k, который может быть легко получен из последних T(...) срок.

---

Для этого нам нужно найти разумное обязательное условие на последний срок. Это можно сделать, попробовав пару целых чисел, таких как 0, 1, 2, С 2 у тебя есть:

---

Подставляя k в наше предыдущее уравнение, вы увидите, что самый большой член равен:

и, следовательно, сложность:

PS вы можете увидеть решение подобного повторения здесь