Как построить неравенства

Question

Я хотел бы построить следующие неравенства:y < p₂(1 - p₁) и x < p₁(1 - (y / (1 - p₁))).

Учитывая, что первое удовлетворено, я хочу построить регион, в котором оба удовлетворены.
p₁ и p₂ могут варьироваться в пределах [0,1].

Буду признателен за любую помощь!

Answer 1

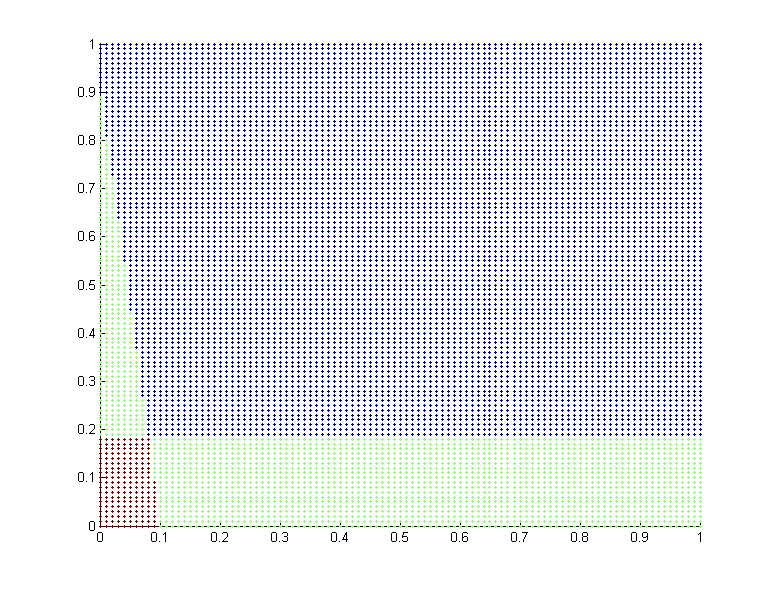
Попробуйте это: красная область - то, где оба неравенства удовлетворены.

[X,Y]=meshgrid(0:0.01:1,0:0.01:1); % Make a grid of points between 0 and 1
p1=0.1; p2=0.2; % Choose some parameters
ineq1 = Y<p2*(1-p1);
ineq2 = X<p1*(1-(Y./(1-p1)));
colors = zeros(size(X))+ineq1+ineq2;
scatter(X(:),Y(:),3,colors(:),'filled')

Answer 2

Альтернативное решение (но похожее на Сэма Роберта) будет использовать contourf:

[X, Y] = meshgrid((0:999) / 1000, (0:999) / 1000);
p = rand(2, 1);                            %# In this example p = [0.1, 0.2]
ineq1 = Y < p(2) * (1 - p(1));             %# First inequation
ineq2 = X < p(1) * (1 - (Y / (1 - p(1)))); %# Second inequation
both = ineq1 & ineq2;                      %# Intersection of both inequations

figure, hold on
c = 1:3;                                   %# Contour levels
contourf(c(1) * ineq1, [c(1), c(1)], 'b')  %# Fill area for first inequation
contourf(c(2) * ineq2, [c(2), c(2)], 'g')  %# Fill area for second inequation
contourf(c(3) * both, [c(3), c(3)], 'r')   %# Fill area for both inequations
legend('First', 'Second', 'Both')
set(gca, ...                               %# Fixing axes ticks
    'XTickLabel', {t(get(gca, 'XTick'))}, 'YTickLabel', {t(get(gca, 'YTick'))})

и вот результат:

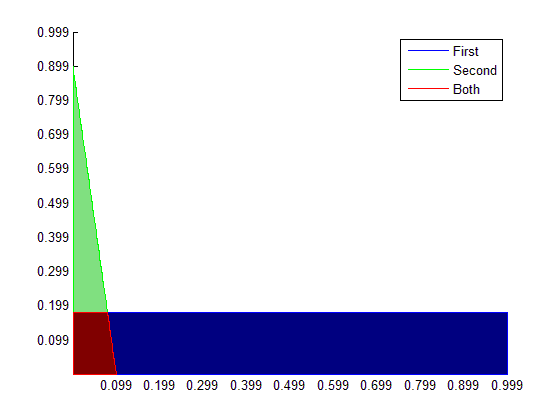
Красная область (как указано в легенде) указывает, где выполняются оба неравенства.

Обратите внимание, что второй и третий contourf звонки только для иллюстрации, чтобы показать, где выполняется только одно из неравенств.

Answer 3

Я думаю, что этот метод легко понять. Сделайте участок поверхности и поверните его к виду сверху.

v = -5:0.1:5;
p1 = 0.1;
p2 = 0.2;
[x,y] = meshgrid(v);
ineq1 = y<p2*(1-p1);
ineq2 = x<p1*(1-(y./(1-p1)));
ineq = double(ineq1 & ineq2);    % intersection of the inequalities
surf(x,y,ineq);
view(0,90)      % rotate surface plot to top view