Непрерывное преобразование PowerTransform/BoxCox в R

Question

У меня есть набор данных, который мне нужно перенести в нормальное распределение.

Во-первых, создать воспроизводимый набор данных.

df <- runif(500, 0, 100)

Во-вторых, определите функцию. Эта функция продолжит преобразование df, пока P > 0,05. Преобразованный df будет сгенерирован и назван как y.

BoxCoxTrans <- function(y)    
{
    lambda <- 1
    constant <- 0
    while(shapiro.test(y)$p.value < 0.10) 
    {
        constant <- abs(min(y, na.rm = TRUE)) + 0.001
        y <- y + constant
        lambda <- powerTransform(y)$lambda
        y <- y ^ lambda
    }
    assign("y", y, envir = .GlobalEnv) 
}

В-третьих, тест дф

shapiro.test(df)

Shapiro-Wilk normality test

data:  df
W = 0.95997, p-value = 2.05e-10

Поскольку P < 0,05, преобразование df

BoxCoxTrans(df)

Затем он дает мне следующие сообщения об ошибках,

Error in qr.resid(xqr, w * fam(Y, lambda, j = TRUE)) : 
NA/NaN/Inf in foreign function call (arg 5)

Что я сделал не так?

Answer 1

Вы можете использовать преобразование Бокса-Мюллера для генерации приблизительно нормального распределения из случайного равномерного распределения. Это может быть более подходящим, чем преобразование Бокса-Кокса, которое AFAIK обычно применяется для преобразования искаженного распределения в почти нормальное.

Вот пример преобразования Бокса-Мюллера, примененного к набору равномерно распределенных чисел:

set.seed(1234)
size <- 5000
a <- runif(size)
b <- runif(size)
y <- sqrt(-2 * log(a)) * cos(2 * pi * b)
plot(density(y), main = "Example of Box-Muller Transformation", xlab="x", ylab="f(x)")
library(nortest)
#> lillie.test(y)
#
#   Lilliefors (Kolmogorov-Smirnov) normality test
#
#data:  y
#D = 0.009062, p-value = 0.4099
#
#> shapiro.test(y)
#
#   Shapiro-Wilk normality test
#
#data:  y
#W = 0.99943, p-value = 0.1301
#

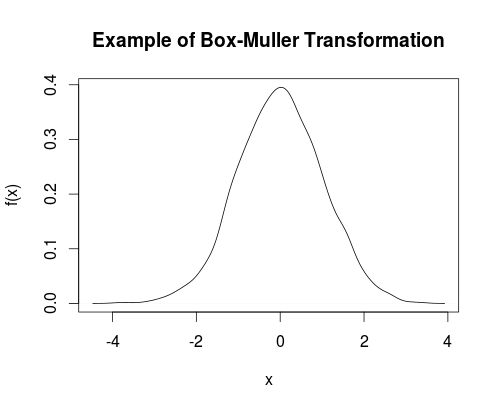
Надеюсь это поможет.

Answer 2

Добавлять

 print(summary(y))

до конца вашего while цикл и смотреть, как ваши вычисления взрываются. В любом случае, повторное применение Box-Cox не имеет смысла, потому что вы получаете ML(-подобную) оценку параметра преобразования из первого приложения. Кроме того, почему вы ожидаете, что преобразование мощности нормализует равномерное распределение?

Джон