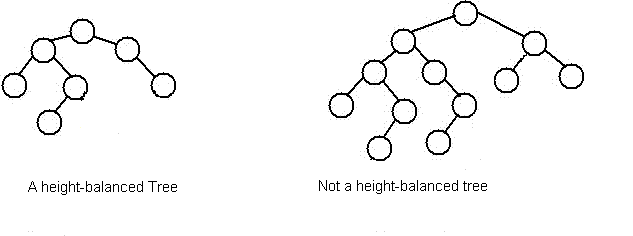
Логическая проверка функции, чтобы найти сбалансированное или несбалансированное дерево

Question

Я читаю книгу по кодированию, и один из вопросов просит написать функцию, которая проверяет, сбалансирована ли высота двоичного дерева или нет. Например, если правое поддерево дерева имеет высоту 4 (что означает, что его глубина равна 4), а левое поддерево имеет глубину 6, то оно не сбалансировано, но если оно выключено на 1, то это нормально.

Итак, я реализовал эту логику:

int FindNodeHeight(BTNode<int>* node) {

    if(!node)  return 0;
    return std::max(FindNodeHeight(node->lhs), FindNodeHeight(node->rhs)) + 1;
}

bool IsTreeBalanced(BinarySearchTree<int>* root) {

    int left = FindNodeHeight(root->root.lhs);
    int right = FindNodeHeight(root->root.rhs);

    std::cout << "left: " << left << " - right: " << right << std::endl;

    if(std::abs(left - right) > 1) {
        return false;
    }

    return true;
}

Но я думаю, что это может быть неправильно на основе объяснения решений, но я не понимаю, почему. Вот упрощенные классы:

template <typename T>
// Binary Tree Node
class BTNode {
public:
    T data;
    BTNode* lhs;
    BTNode* rhs;

    BTNode() {
        lhs = NULL;
        rhs = NULL;
    }
};

template <typename T>
class BinarySearchTree {
public:
    BTNode<T> root;
};

И вот главное, где создается граф и вызывается функция:

BinarySearchTree<int>* t_unbalanced = new BinarySearchTree<int>();
t_unbalanced->root.data = 1;
t_unbalanced->root.lhs = new BTNode<int>(2);
t_unbalanced->root.rhs = new BTNode<int>(3);
t_unbalanced->root.rhs->rhs = new BTNode<int>(4);
t_unbalanced->root.rhs->rhs->rhs = new BTNode<int>(5);

if(IsTreeBalanced(t_unbalanced)) {
    cout << "Tree is balanced" << endl;
}
else {
    cout << "Tree is unbalanced" << endl;
}

Answer 1

Рассмотрим следующий случай:

            x
           / \
          x   x
         /     \
        x       x
       /         \
      x           x
     /             \
    .               .
   .                 .
  .                   .
 /                     \
x                       x

Ваш алгоритм утверждает, что дерево сбалансировано, потому что высота левого дерева равна высоте правого дерева. Однако высота дерева n/2=theta(n)!=O(log(n)), Поэтому дерево не сбалансировано.

Сбалансированные деревья поиска - это деревья, высота которых в худшем случае составляет O(logn) и для которых операции INSERT, DELETE и SEARCH могут быть реализованы за время O(logn).

Смотрите источник.