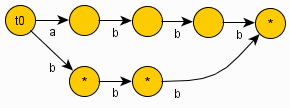
Что такое суффикс автомат?
Может кто-нибудь объяснить мне, что такое суффиксный автомат, и как он работает и отличается от суффиксных деревьев и суффиксных массивов? Я уже пробовал поиск в Интернете, но не смог найти четкого исчерпывающего объяснения.
Я нашел следующую ссылку ближе к тому, что я хотел, но она на русском языке, и перевод на английский было трудно понять.
2 ответа
Суффиксный автомат - это конечный автомат, который распознает все суффиксы строки. Есть много ресурсов о машинах с конечным числом состояний, которые вы можете прочитать, Википедия - хорошее начало.
Суффиксные деревья и суффиксные массивы - это структуры данных, содержащие все суффиксы строки. Существует множество алгоритмов для построения и работы с этими структурами для эффективного выполнения операций над строками.
Суффикс Машина:
Суффикс-машина (или ориентированный ациклический граф слов) - это мощная структура данных, которая позволяет решать многие строковые задачи.
Например, используя суффикс машины, вы можете искать все вхождения одной строки в другую или подсчитывать количество различных подстрок данной строки - обе задачи она может решать за линейное время.
На интуитивном уровне под суффиксным автоматом можно понимать краткую информацию обо всех подстроках данной строки. Впечатляет тот факт, что суффиксный автомат содержит всю информацию в такой сжатой форме, которая для строки длины n требует только O(n) памяти. Более того, он также может быть построен с течением времени O(n) (если мы рассмотрим размер алфавита k постоянным; в противном случае, во время O (n log k)).
Исторически первый суффикс линейного размера машины был открыт в 1983 году Блюмером и другими, а в 1985 - 1986 годах ему были представлены первые алгоритмы построения в линейном времени (Крочемор, Блумер и другие). Для получения более подробной информации см. Ссылки в конце статьи.
В английском языке суффикс-машина называется "суффикс-автомат" (во множественном числе - "суффикс-автомат") и ориентированный ациклический граф слов "направленный ациклический граф слов (или просто"DAWG").
Определение суффиксного автомата:
Определение. Суффиксный автомат для данной строки s называется минимальным детерминированным конечным автоматом, который принимает все суффиксы строки s.
Мы объясним это определение.
- Суффиксный автомат - это ориентированный ациклический граф, в котором вершины называются состояниями, а дуги графа - это переходы между
эти состояния.- Одно из состояний t_0 называется начальным состоянием, и оно должно быть источником графа (т. Е. Оно достижимо для всех других состояний).
- Каждый переход в автомате отмечен дугой с некоторым символом. Все переходы, происходящие из любого состояния, должны иметь разные метки. (С другой стороны, не может быть переходов ни для каких символов.)
- Одно или несколько условий помечены как терминальные состояния. Если мы переходим из начального состояния t_0 любым способом в любое состояние терминала, и давайте
написать эту метку все пройденные дуги, вы получите строку, которая должна быть
один из суффиксов строки s.- Суффиксный автомат содержит минимальное количество вершин среди всех машин, которые удовлетворяют вышеуказанным условиям. (Минимум
количество переходов не требуется, так как условие
минимальность количества состояний в машине не может быть "лишней"
пути - иначе это сломало бы предыдущее свойство.)
Элементарные свойства суффиксного автомата:
Самое простое и, тем не менее, самое важное свойство автомата-суффикса состоит в том, что он содержит информацию обо всех подстроках строки s. А именно, любой путь из начального состояния t_0, если мы выписываем метки дуг вдоль этого пути, обязательно формирует подстроку строки s. Наоборот, любая подстрока строки s соответствует некоторому пути, начинающемуся в начальном состоянии t_0.
Чтобы упростить объяснение, скажем, что подстрока соответствует пути из начального состояния, метки вдоль которого образуют подстроку. Наоборот, мы будем говорить, что любой путь соответствует одной строке, которая образована метками его дуг.
В каждом конечном автомате суффикс представляет собой один или несколько путей из начального состояния. Допустим, что состояние соответствует набору строк, которые соответствуют всем этим способам.
ПРИМЕРЫ: