Как найти две точки вдоль существующей линии

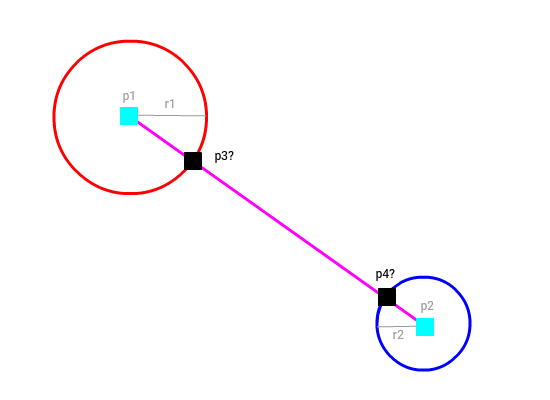
Я уверен, что это базовая тригонометрия, и держу пари, что я учился в школе много лет назад, но я не знаю, какую функцию применять в реальной ситуации. В любом случае, вместо того, чтобы пытаться объяснить, что мне нужно, я нарисовал небольшую диаграмму:

Я знаю p1, p2, r1 и r2, но я не могу вспомнить (или не знаю, как искать), как определить, что такое p3 и p4.

Основное применение этой установки - у меня есть 2 круга (красный и синий), и мне нужно, чтобы они постоянно были связаны, когда я перетаскивал их по холсту. Розовая ссылка соединит их через их центральные точки, но я не хочу, чтобы линия проходила через окружности круга.

Надеюсь, что имеет смысл? Заранее спасибо.

Источник

4 ответа

Решение

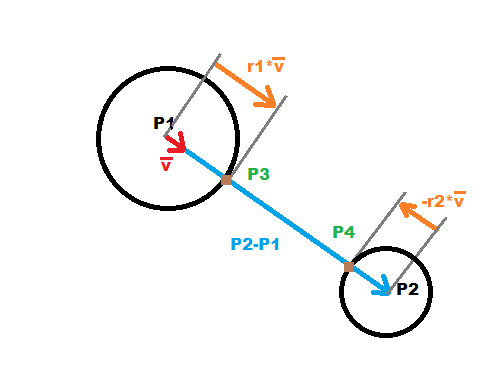
Это простая векторная математика (тригонометрия не требуется)

  1. создать единичный вектор v с P1 в P2 направление

    Это легко в векторной форме:

    v=P2-P1; v/=|v|

    И когда положить в 2D:

    v.x=P2.x-P1.x;
v.y=P2.y-P1.y;
l=sqrt((v.x*v.x)+(v.y*v.y))
v.x/=l;
v.y/=l;

  2. Теперь просто перевести с P1,P2 от r1,r2

    Векторная форма:

    P3=P1+r1*v
P4=P2-r2*v

    В 2D:

    P3.x=P1.x+r1*v.x;
P3.y=P1.y+r1*v.y;
P4.x=P2.x-r2*v.x;
P4.y=P2.y-r2*v.y;

введите описание изображения здесь

Источник

То, что я собираюсь сказать, немного долго. Я позволю вам написать свой собственный код, однако, конечно, не поможет с этим.

Вы знаете точки P1, P2 и радиус R1 и R2. Предположим, что точки P1 и P2 имеют координаты (x1,y1) и (x2,y2) соответственно.

Линия, соединяющая P1 и P2, является прямой линией, и, следовательно, вы можете рассчитать наклон линии, используя формулу m=(y2-y1)/(x2-x1), Так как вы знаете наклон и знаете две координаты, вы можете вычислить точку пересечения c и построить формулу вида y=mx+c,

Как только получится линейная формула, вы можете применить значения для x и вычислить y для точки P3, скажем, x3 и y3, так как у вас есть радиус R1. Аналогичным образом рассчитайте координаты для P4.

Источник

Пусть d будет расстоянием между p1 (x1, y1) и p2 (x2, y2)
Таким образом, d = sqrt((x1-x2)^2 + (y1-y2)^2)
Теперь точка p3 (x3, y3) делит линию между p1 и p2 в соотношении r1:(d-r1)

таким образом
x3 = (r1 * x2 + (d-r1) * x1) / d и
y3 = (r1 * y2 + (d-r1) * y1) / d

Аналогично для p4 (x4, y4)
x4 = (r2 * x1 + (d-r2) * x2) / d и
y4 = (r2 * y1 + (d-r2) * y2) / d

Источник

Вы должны решить следующую систему уравнений:

Для р3 ->

(X-p1x)/(p1x-p2x)=(Y-p1y)/(p1y-p2y)
(X-p1x)^2 + (Y-p1y)^2 = r1^2

То же самое для p4 просто измените r1 для r2 и p1 для p4 во втором уравнении.

Первое уравнение - это уравнение прямой с двумя точками. И второе уравнение - это уравнение окружности с учетом центральной точки и радиуса.

Результирующие значения X, Y будут значениями p3, а затем p4.

Источник
Другие вопросы по тегам