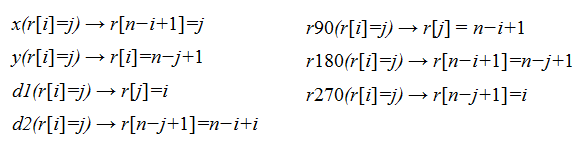Симметрия N-Queens нарушает Google OR Tools

Question

Одним из примеров Google or-tools является решение проблемы n-queens. Внизу написано, что реализацию можно улучшить, добавив ограничения симметрии в решатель ограничений.

Оглядываясь в Интернете, я обнаружил ограничения симметрии для задачи n-ферзей, но я не могу понять, как преобразовать их в ограничения в код Python, который их реализует.

---

РЕДАКТИРОВАТЬ: это был плохой вопрос, давайте обновим...

Что я пробовал?

Вот настройка из первой ссылки выше:

from ortools.constraint_solver import pywrapcp

N = 8
solver = pywrapcp.Solver("n-queens")
# Creates the variables.
# The array index is the column, and the value is the row.
queens = [solver.IntVar(0, N - 1, "x%i" % i) for i in range(N)]
# Creates the constraints.
# All rows must be different.
solver.Add(solver.AllDifferent(queens))
# All columns must be different because the indices of queens are all different.
# No two queens can be on the same diagonal.
solver.Add(solver.AllDifferent([queens[i] + i for i in range(N)]))
solver.Add(solver.AllDifferent([queens[i] - i for i in range(N)]))

# TODO: add symmetry breaking constraints

db = solver.Phase(queens, solver.CHOOSE_FIRST_UNBOUND, solver.ASSIGN_MIN_VALUE)
solver.NewSearch(db)
num_solutions = 0
while solver.NextSolution():
  num_solutions += 1
solver.EndSearch()
print()
print("Solutions found:", num_solutions)
print("Time:", solver.WallTime(), "ms")

Я знаю, что могу успешно реализовать простые ограничения. Если бы я хотел убедиться, что в решении всегда есть ферзь в первом столбце первой строки, я мог бы реализовать это следующим образом:

solver.Add(queens[0] == 0)

queens[0] Переменная представляет местоположение королевы в первом столбце, и это ограничение выполняется только тогда, когда в первом столбце есть ферзь в первой строке. Это, конечно, не то, что я хочу сделать, потому что возможно, что решение не содержит угловых ячеек.

Ограничения нарушения симметрии для задачи n-ферзей приведены ниже. Они вытягиваются прямо из ссылки во втором абзаце.

Я понимаю, как работают эти ограничения. Идея состоит в том, что вы можете применить эту функцию к каждой ячейке на доске n-ферзей, чтобы преобразовать состояние в эквивалентное состояние. Одним из этих состояний будет каноническое представление этого состояния. Это используется в качестве метода сокращения будущей обработки путем исключения дублирующих оценок.

Если бы я просто реализовывал это после фактов, я бы сделал именно то, что я описал выше, преобразовал бы состояние, используя каждую возможную функцию нарушения симметрии, вычислил какой-нибудь хэш состояния (например, строку выбранной строки в каждом столбце). и выберите тот, который является самым низким для каждого предложенного решения. Пропустите будущую обработку тех, что мы видели раньше.

Моя проблема в том, что я не знаю, как преобразовать эти преобразования в ограничения для решателя программирования ограничений Google или-tools.

Давайте посмотрим на самый простой, d1(r[i] = j) => r[j] = i, размышления о главной диагонали. Что я знаю, так это то, что преобразование должно применяться ко всем ячейкам, а затем сравниваться с текущим состоянием, чтобы предотвратить его расширение. Я не достаточно разбираюсь в python, чтобы понять, какое выражение работает здесь для преобразования, и я просто не могу понять, как создать ограничение, которое сравнивает преобразование с текущим состоянием для этого конкретного решателя.

state = [queens[i].Value() for i in range(N)]
symX    = [state[N - (i + 1)] for i in range(N)]
symY    = [N - (state[i] + 1) for i in range(N)]
symD1   = [state.index(i) for i in range(N)]
symD2   = [N - (state.index(N-(i+1)) + 1) for i in range(N)]
symR90  = [N - (state.index(i) + 1) for i in range(N)]
symR180 = [N - (state[N-(i+1)] + 1) for i in range(N)]
symR270 = [state.index(N-(i+1)) for i in range(N)]

Answer 1

Я пытался использовать пользовательский DecisionBuilder для обрезки дерева поиска, используя симметрии в качестве новых ограничений, но я не мог заставить его работать.

Вместо этого мне пришлось использовать SearchMonitor, который фиксирует событие каждого решения и проверить, является ли это решение симметрией предыдущего.

Здесь я добавляю код SearchMonitor, захват решения, перекрывающего функцию "AcceptSolution", и функцию gen_symetries для вычисления и проверки всех возможных симметрий.

    class SearchMonitor(pywrapcp.SearchMonitor):
    def __init__(self, solver, q):
        pywrapcp.SearchMonitor.__init__(self, solver)
        self.q = q
        self.all_solutions = []
        self.unique_solutions = []
        self.n = len(self.q)

    def AcceptSolution(self):
        qval = [self.q[i].Value() for i in range(self.n)]
        self.all_solutions.append(qval)

        symmetries = [vv in self.unique_solutions for vv in gen_symmetries(self.n, qval)]

        if sum(symmetries) == 0:
            self.unique_solutions.append(qval)

        return False

def gen_symmetries(n, solution):
    symmetries = []

    #x(r[i]=j) → r[n−i+1]=j
    x = list(range(n))
    for index in range(n):
        x[n - 1 - index] = solution[index]

    symmetries.append(x)

    #y(r[i]=j) → r[i]=n−j+1
    y = list(range(n))
    for index in range(n):
        y[index] = (n - 1 - solution[index])

    symmetries.append(y)

    #d1(r[i]=j) → r[j]=i
    d1 = list(range(n))
    for index in range(n):
        d1[solution[index]] = index

    symmetries.append(d1)

    # d2(r[i]=j) → r[n−j+1]=n−i+1
    d2 = list(range(n))
    for index in range(n):
        d2[n - 1 - solution[index]] = (n - 1 - index)

    symmetries.append(d2)

    # r90(r[i]=j) → r[j] = n−i+1
    r90 = list(range(n))
    for index in range(n):
        r90[solution[index]] = (n - 1 - index)

    symmetries.append(r90)

    # r180(r[i]=j) → r[n−i+1]=n−j+1
    r180 = list(range(n))
    for index in range(n):
        r180[n - 1 - index] = (n - 1 - solution[index])

    symmetries.append(r180)

    # r270(r[i]=j) → r[n−j+1]=i
    r270 = list(range(n))
    for index in range(n):
        r270[n - 1 - solution[index]] = index

    symmetries.append(r270)

    return symmetries

Позже вам просто нужно добавить монитор в ваш решатель, как это.

monitor = SearchMonitor(solver, queens)
solver.Solve(db, monitor)
solver.NewSearch(db)

И, наконец, просто распечатать все уникальные решения

print("Unique Solutions:", len(monitor.unique_solutions), monitor.unique_solutions)

Вы можете увидеть полный рабочий пример в сущности.

https://gist.github.com/carlgira/7a4e6cf0f7b7412762171015917bccb4

Answer 2

Вы должны использовать известные отношения симметрии между искомыми решениями, чтобы идентифицировать ограничения, которые устранят эквивалентные решения.

1. Для каждого решения с queens[0] >= N/2то есть другое, вертикально отраженное, решение с queens[0] <= N/2, Поэтому мы можем искать решение с меньшим значением queens[0] и добавьте следующее ограничение:

   solver.Add(queens[0] < (N+1)//2) # Handle both even and odd values of N
   

2. Тогда решение, удовлетворяющее условию queens[0] < queens[N-1] имеет эквивалентное горизонтально-зеркальное решение, удовлетворяющее queens[0] > queens[N-1], Вы можете указать решающему искать только те решения, в которых ферзь в крайнем левом столбце находится под королевой в крайнем правом столбце:

   solver.Add(queens[0] < queens[N-1])
   

Я не мог легко сформулировать ограничение, отражающее симметрию вращения, но я считаю, что это возможно.