Реконструкция цифрового сигнала с использованием функции sinc

Question

Я пытаюсь восстановить сигнал cos(2*pi*300e6) на частоте дискретизации 800e6, используя функцию sinc в MATLAB. Когда я набираю следующий код, я получаю что-то очень шумное - не то, что я ищу. Что я делаю неправильно? Заранее спасибо!

Код:

F1 = 300e6;
Fs = 800e6;
tmin = 0;
tmax = 10/F1;
t = tmin:1e-12:tmax;
x1 = cos(2*pi*F1*t);
Ts = 1/Fs;
ts = tmin:Ts:tmax;
x1resampled = cos(2*pi*F1*ts);
x1reconstructed = zeros(1,length(t)); %preallocating for speed
samples = length(ts);
for i = 1:1:length(t)
    for n = 1:1:samples
        x1reconstructed(i) = sum(x1resampled(n)*sinc(pi*(t(i)-n*Ts)/Ts));
    end
end
figure(1)
subplot(2,1,1)
plot(t,x1)
hold on
stem(ts,x1resampled)
subplot(2,1,2)
plot(t,x1reconstructed)

Answer 1

Две проблемы с кодом:

1. Вы не накапливаете восстановленные образцы должным образом. В частности, вы сохраняете только одно значение из передискретизированного сигнала, а не все выборки.

2. sinc в MATLAB используется нормализованная функция sinc. Это означает, что вам не нужно умножать аргумент на pi, Напомним, что для формулы восстановления требуется нормализованная функция sinc, поэтому нет умножения pi в аргументе функции.

Поэтому вы просто должны изменить код внутри for цикл:

F1 = 300e6;
Fs = 800e6;
tmin = 0;
tmax = 10/F1;
t = tmin:1e-12:tmax;
x1 = cos(2*pi*F1*t);
Ts = 1/Fs;
ts = tmin:Ts:tmax;
x1resampled = cos(2*pi*F1*ts);
x1reconstructed = zeros(1,length(t)); %preallocating for speed
samples = length(ts);
for i = 1:1:length(t)
    for n = 1:1:samples
        x1reconstructed(i) = x1reconstructed(i) + x1resampled(n)*sinc((t(i)-n*Ts)/Ts); %%% CHANGE
    end
end
figure(1)
subplot(2,1,1)
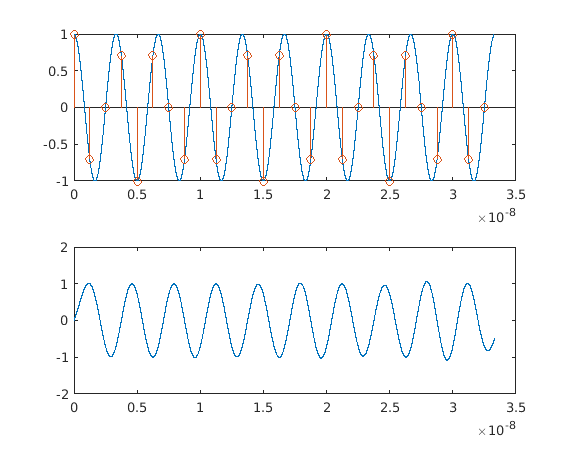
plot(t,x1)
hold on
stem(ts,x1resampled)
subplot(2,1,2)
plot(t,x1reconstructed)

Теперь я получаю этот сюжет:

Чтобы сделать вещи более эффективными, обязательно используйте sum функция, но сделать это по всем образцам. Так что ваши for Цикл теперь должен быть:

for i = 1:1:length(t)
    x1reconstructed(i) = sum(x1resampled .* sinc((t(i) - (1:samples)*Ts) ./ Ts));
end

Answer 2

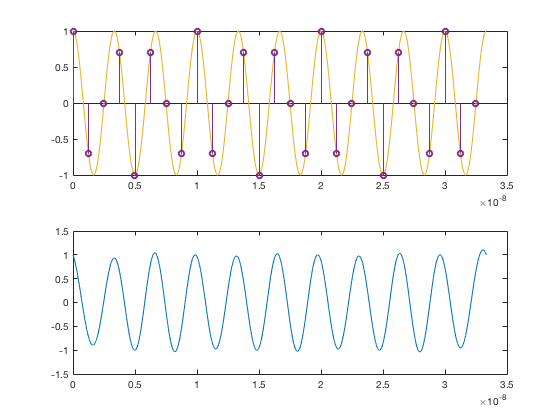
Вы можете сделать то же самое, но более эффективно, используя дискретное преобразование Фурье (DFT):

F1 = 300e6;
Fs = 800e6;
tmin = 0;
tmax = 10/F1;
t = tmin:1e-12:tmax;
x1 = cos(2*pi*F1*t);
Ts = 1/Fs;
ts = tmin:Ts:tmax;
x1resampled = cos(2*pi*F1*ts);

x1resampledDFT = fftshift(fft(x1resampled));
n = (length(x1)-length(x1resampledDFT))/2;
x1reconstructedDFT = [zeros(1,ceil(n)),x1resampledDFT,zeros(1,floor(n))];
x1reconstructed = ifft(ifftshift(x1reconstructedDFT));
x1reconstructed = x1reconstructed / length(x1resampled) * length(x1reconstructed);

figure(1)
subplot(2,1,1)
plot(t,x1)
hold on
stem(ts,x1resampled)
subplot(2,1,2)
plot(t,x1reconstructed)

То, что здесь происходит, это то, что я дополняю DFT (как эффективно вычисляется с использованием fft) с нулями до нужного размера. Затем обратное преобразование приводит к интерполяции сигнала с использованием интерполятора sinc. Для сохранения уровня сигнала необходима некоторая нормализация. Любые различия, которые вы видите в ответе Райриенга, связаны с периодической природой ДПФ: в основном функции sinc, выходя из области сигнала справа, возвращаются слева; данные в правом конце графика влияют на результат в левом конце графика и наоборот.

Чтобы узнать больше об интерполяции с использованием преобразования Фурье, см. Этот пост в блоге.