Отображение n итераций функции - Python

Question

Я изучаю динамические системы, в частности, логистическое семейство g(x) = cx(1-x), и мне нужно повторять эту функцию произвольное количество раз, чтобы понять ее поведение. У меня нет проблем с итерацией функции по заданной точке x_0, но, опять же, я хотел бы построить график всей функции и ее итераций, а не только одной точки. Для построения одной функции у меня есть этот код:

import numpy as np
import scipy as sp
import matplotlib.pyplot as plt

def logplot(c, n = 10):
    dt = .001
    x = np.arange(0,1.001,dt)
    y = c*x*(1-x)
    plt.plot(x,y)
    plt.axis([0, 1, 0, c*.25 + (1/10)*c*.25])
    plt.show()

Я полагаю, что я мог бы решить эту проблему длинным / пугающим методом явного создания списка диапазонов каждой итерации, используя что-то вроде следующего:

def log(c,x0):
    return c*x0*(1-x)

def logiter(c,x0,n):
    i = 0
    y = []
    while i <= n:
        val = log(c,x0)
        y.append(val)
        x0 = val
        i += 1
    return y

Но это кажется действительно громоздким, и мне было интересно, есть ли лучший способ. Спасибо

Answer 1

Несколько разных вариантов

Это действительно вопрос стиля. Ваше решение работает и не очень сложно понять. Если вы хотите продолжать в том же духе, то я бы немного подправил:

def logiter(c, x0, n):
    y = []
    x = x0
    for i in range(n):
        x = c*x*(1-x)
        y.append(x)

    return np.array(y)

Перемены:

• цикл for легче читать, чем цикл while
• x0 не используется в итерации (это добавляет еще одну переменную, но ее математически легче понять; x0 - это константа)
• функция записана, так как это очень простая однострочная строка (если это не так, ее имя должно быть изменено на что-то другое, чем logчто очень легко спутать с логарифмом)
• результат конвертируется в numpy массив. (Что я обычно делаю, если мне нужно что-то построить)

На мой взгляд, функция теперь достаточно разборчива.

Вы также можете использовать объектно-ориентированный подход и создать объект логистической функции:

class Logistics():
    def __init__(self, c, x0):
        self.x = x0
        self.c = c

    def next_iter(self):
        self.x = self.c * self.x * (1 - self.x)
        return self.x

Тогда вы можете использовать это:

 def logiter(c, x0, n):
    l = Logistics(c, x0)
    return np.array([ l.next_iter() for i in range(n) ])

Или, если вы можете сделать это генератором:

def log_generator(c, x0):
    x = x0
    while True:
        x = c * x * (1-x)
        yield x

def logiter(c, x0, n):
    l = log_generator(c, x0)
    return np.array([ l.next() for i in range(n) ])

Если вам нужна производительность и у вас большие таблицы, тогда я предлагаю:

def logiter(c, x0, n):
    res = np.empty((n, len(x0)))
    res[0] = c * x0 * (1 - x0)
    for i in range(1,n):
        res[i] =  c * res[i-1] * (1 - res[i-1])
    return res    

Это позволяет избежать медленного преобразования в np.array и некоторое копирование вещей вокруг. Память выделяется только один раз, и исключается дорогостоящее преобразование из списка в массив.

(Кстати, если вы вернули массив с начальным x0 как первый ряд, последняя версия будет выглядеть чище. Теперь первый должен быть рассчитан отдельно, если желательно избежать копирования вектора.)

---

Какой из них лучше? Я не знаю. ИМО, все читабельно и оправданно, это вопрос стиля. Тем не менее, я говорю только на очень испорченном и плохом Pythonic, поэтому могут быть веские причины, почему еще что-то лучше или почему что-то из вышеперечисленного не очень хорошо!

Спектакль

О производительности: На моей машине я попробовал следующее:

logiter(3.2, linspace(0,1,1000), 10000)

Для первых трех заходов время практически одинаковое, примерно 1,5 с. Для последнего подхода (предварительно выделенный массив) время выполнения составляет 0,2 с. Однако, если преобразование из списка в массив удаляется, первый выполняется за 0,16 с, поэтому время действительно затрачивается на процедуру преобразования.

Визуализация

Я могу придумать два полезных, но совершенно разных способа визуализации функции. Вы упоминаете, что у вас будет, скажем, 100 или 1000 разных х0 для начала. Вы не упоминаете, сколько итераций вы хотите иметь, но, возможно, мы начнем с всего лишь 100. Итак, давайте создадим массив из 100 различных x0 и 100 итераций при c = 3.2.

data = logiter(3.6, np.linspace(0,1,100), 100)

В некотором смысле стандартным способом визуализации функции является рисование 100 линий, каждая из которых представляет одно начальное значение. Это просто:

import matplotlib.pyplot as plt

plt.plot(data)
plt.show()

Это дает:

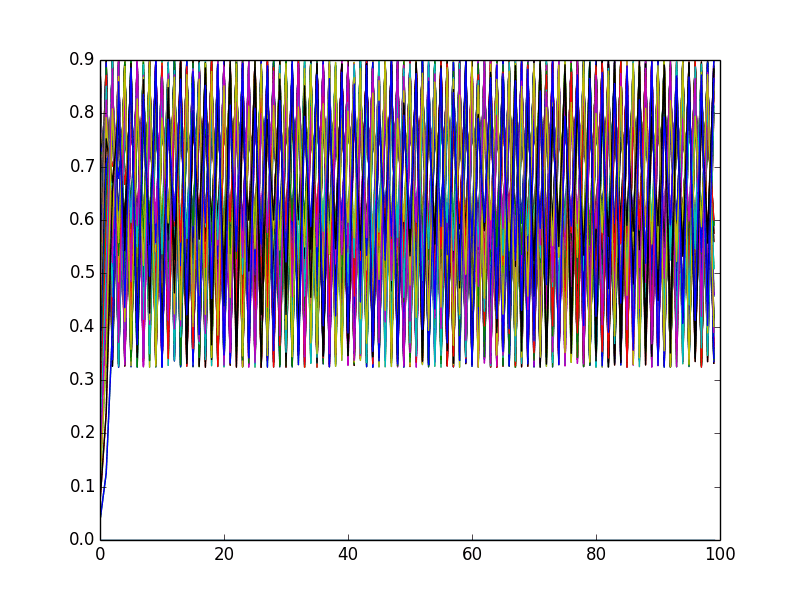
Ну, кажется, что все значения где-то колеблются, но в остальном у нас только цветовой беспорядок. Этот подход может быть более полезным, если вы используете более узкий диапазон значений для x0:

data = logiter(3.6, np.linspace(0.8,0.81,100), 100)

Вы можете закрасить начальные значения, например:

color1 = np.array([1,0,0])
color2 = np.array([0,0,1])
for i,k in enumerate(np.linspace(0, 1, data.shape[1])):
    plt.plot(data[:,i], '.', color=(1-k)*color1 + k*color2)

Это отображает первые столбцы (соответствующие x0 = 0,80) красным и последние столбцы синим цветом и использует постепенное изменение цвета между ними. (Обратите внимание, что чем больше синяя точка, тем позже она рисуется, и, следовательно, синий цвет перекрывает красные.)

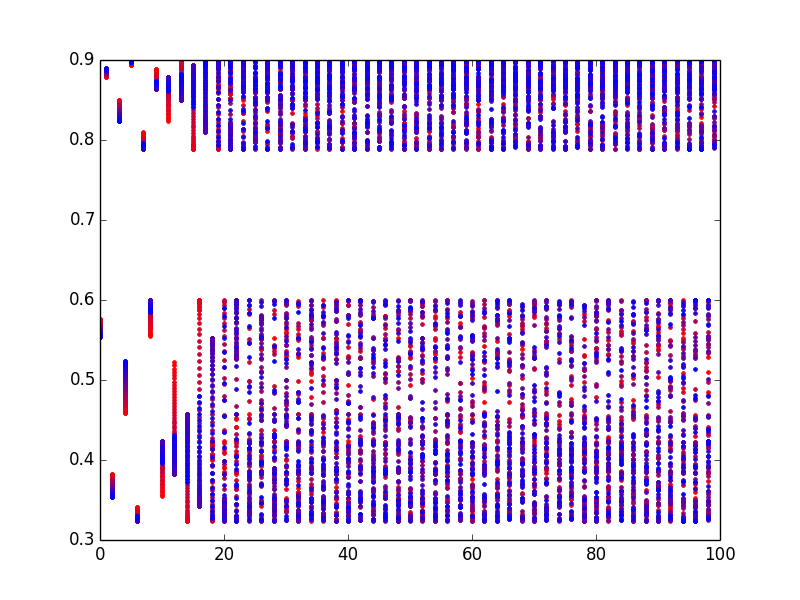
Тем не менее, можно использовать совершенно другой подход.

data = logiter(3.6, np.linspace(0,1,1000), 50)
plt.imshow(data.T, cmap=plt.cm.bwr, interpolation='nearest', origin='lower',extent=[1,21,0,1], vmin=0, vmax=1)
plt.axis('tight')
plt.colorbar()

дает:

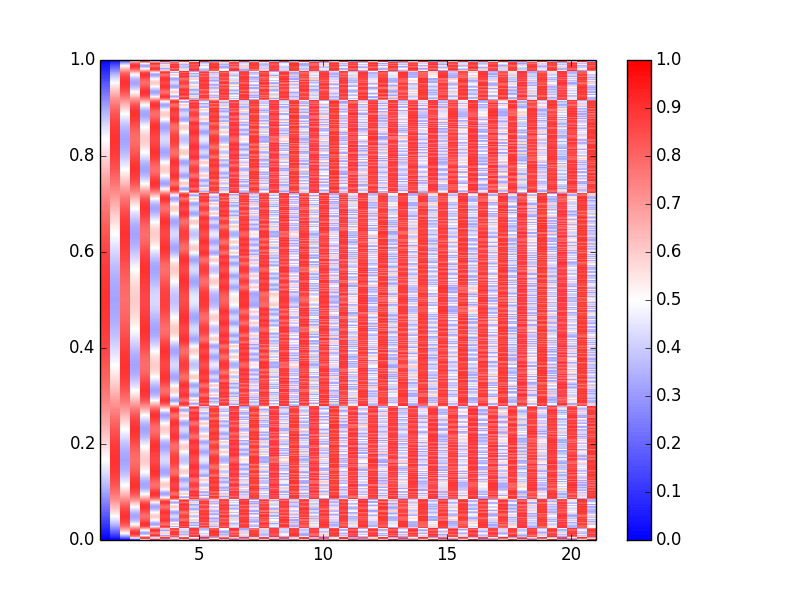
Это мой личный фаворит. Я не испорчу чью-либо радость, объясняя это слишком много, но, по-моему, это очень легко показывает многие особенности поведения.

Answer 2

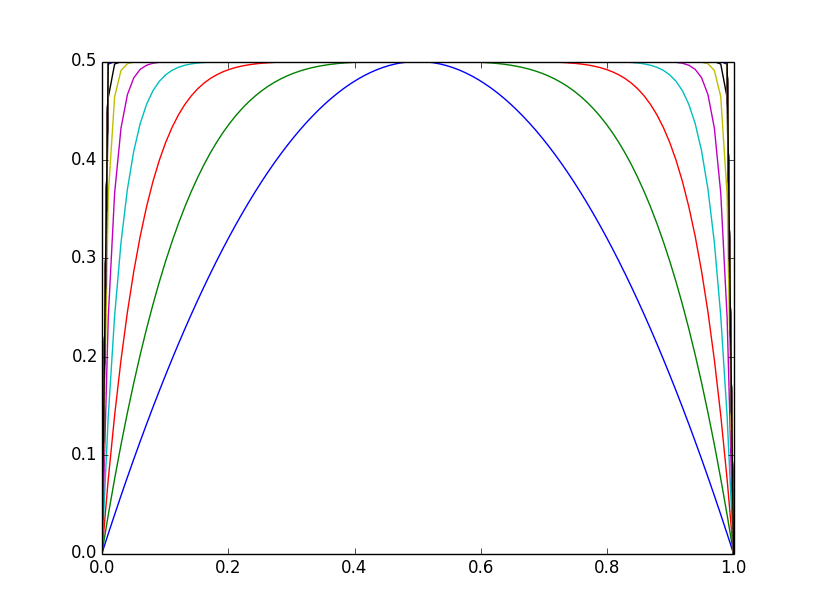
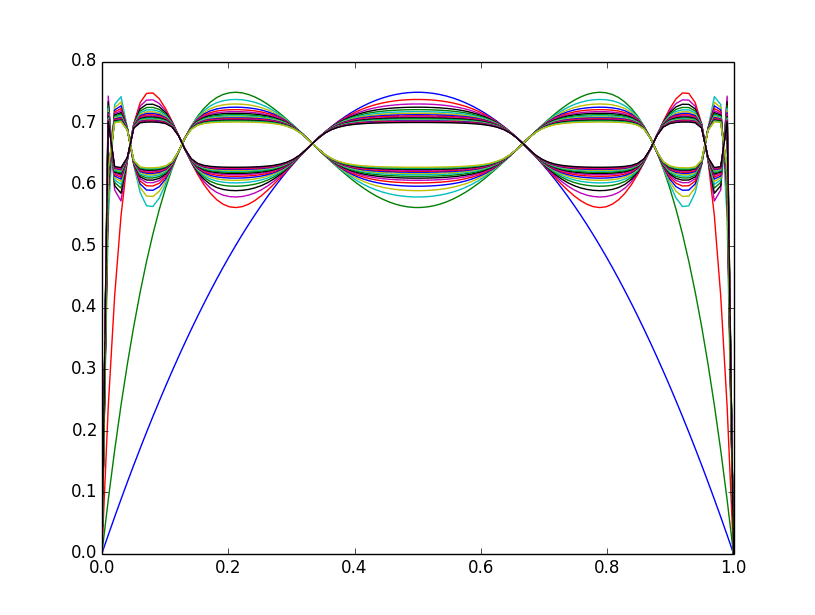
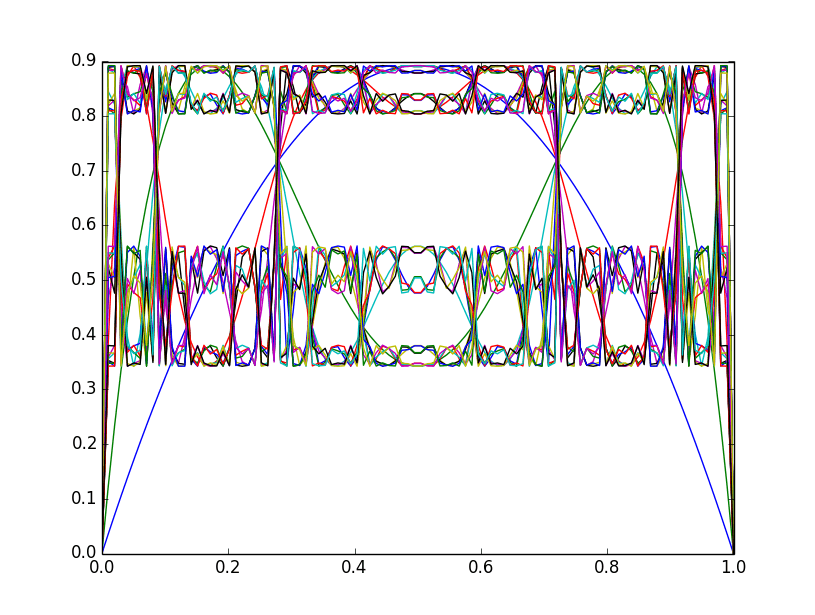
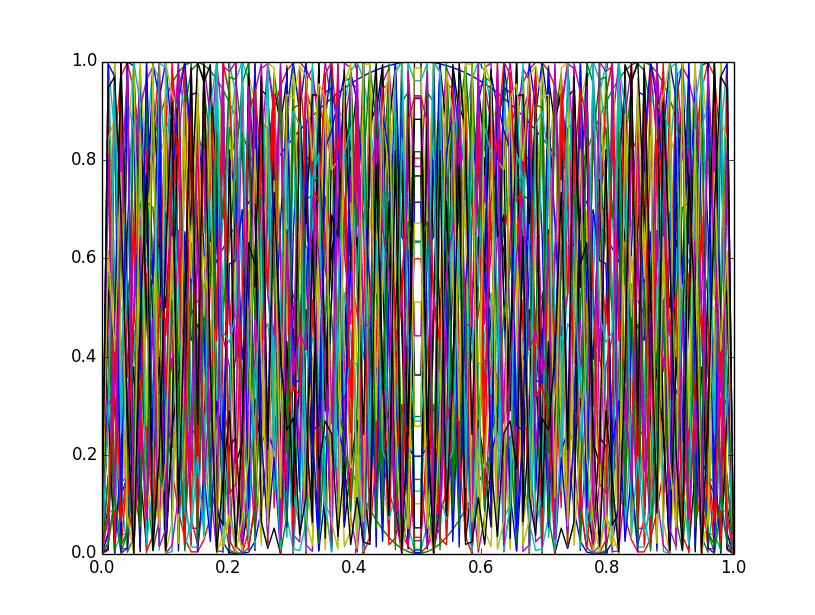
Вот к чему я стремился; косвенный подход к пониманию (путем визуализации) поведения начальных условий функции g (c, x) = cx(1-x):

def jam(c, n):

    x = np.linspace(0,1,100)
    y = c*x*(1-x)
    for i in range(n):
        plt.plot(x, y)
        y = c*y*(1-y)

    plt.show()