Как сгладить ecdf-графики в r
У меня есть df с 5 переменные,
головка (DF,15)
junc N1.ir N2.ir W1.ir W2.ir W3.ir
1 pos$chr1:3197398 0.000000 0.000000 0.000000 0.000000 0.000000
2 pos$chr1:3207049 0.000000 0.000000 0.000000 0.000000 0.000000
3 pos$chr1:3411982 0.000000 0.000000 0.000000 0.000000 0.000000
4 pos$chr1:4342162 0.000000 0.000000 0.000000 0.000000 0.000000
5 pos$chr1:4342918 0.000000 0.000000 0.000000 0.000000 0.000000
6 pos$chr1:4767729 -4.369234 -5.123382 -4.738768 -4.643856 -5.034646
7 pos$chr1:4772814 -3.841302 -3.891419 -4.025029 -3.643856 -3.184425
8 pos$chr1:4798063 -5.038919 -4.847997 -5.497187 -4.035624 -7.543032
9 pos$chr1:4798567 -4.735325 -5.096862 -3.882643 -3.227069 -4.983808
10 pos$chr1:4818730 -8.366322 -7.118941 -8.280771 -6.629357 -6.876517
11 pos$chr1:4820396 -5.514573 -6.330917 -5.898853 -4.700440 -5.830075
12 pos$chr1:4822462 -5.580662 -6.914883 -5.562242 -5.380822 -5.703211
13 pos$chr1:4827155 -4.333273 -4.600904 -4.133399 -4.012824 -3.708345
14 pos$chr1:4829569 -4.287866 -3.874469 -3.977280 -4.209453 -4.490326
15 pos$chr1:4857613 -6.902074 -6.074141 -6.116864 -3.989946 -6.474259
Несколько строк после использования melt
> head(ir.m)
junc variable value
1 pos$chr1:3197398 N1.ir 0.000000
2 pos$chr1:3207049 N1.ir 0.000000
3 pos$chr1:3411982 N1.ir 0.000000
4 pos$chr1:4342162 N1.ir 0.000000
5 pos$chr1:4342918 N1.ir 0.000000
6 pos$chr1:4767729 N1.ir -4.369234
И резюме
> summary(ir)
junc N1.ir N2.ir W1.ir
neg$chr1:100030088: 1 Min. :-11.962 Min. :-12.141 Min. :-11.817
neg$chr1:100039873: 1 1st Qu.: -4.379 1st Qu.: -4.217 1st Qu.: -4.158
neg$chr1:10023338 : 1 Median : -2.807 Median : -2.663 Median : -2.585
neg$chr1:10024088 : 1 Mean : -2.556 Mean : -2.434 Mean : -2.362
neg$chr1:10025009 : 1 3rd Qu.: 0.000 3rd Qu.: 0.000 3rd Qu.: 0.000
neg$chr1:10027750 : 1 Max. : 17.708 Max. : 16.162 Max. : 16.210
(Other) :113310
W2.ir W3.ir
Min. :-12.194 Min. :-11.880
1st Qu.: -3.078 1st Qu.: -4.087
Median : -1.000 Median : -2.711
Mean : -1.577 Mean : -2.370
3rd Qu.: 0.000 3rd Qu.: 0.000
Max. : 17.562 Max. : 16.711
Я пытаюсь построить кумулятивную вероятность, используя ggplot а также stat_ecdf,
используя этот код
ggplot(ir.m, aes(x=value)) + stat_ecdf(aes(group=variable,colour = variable))
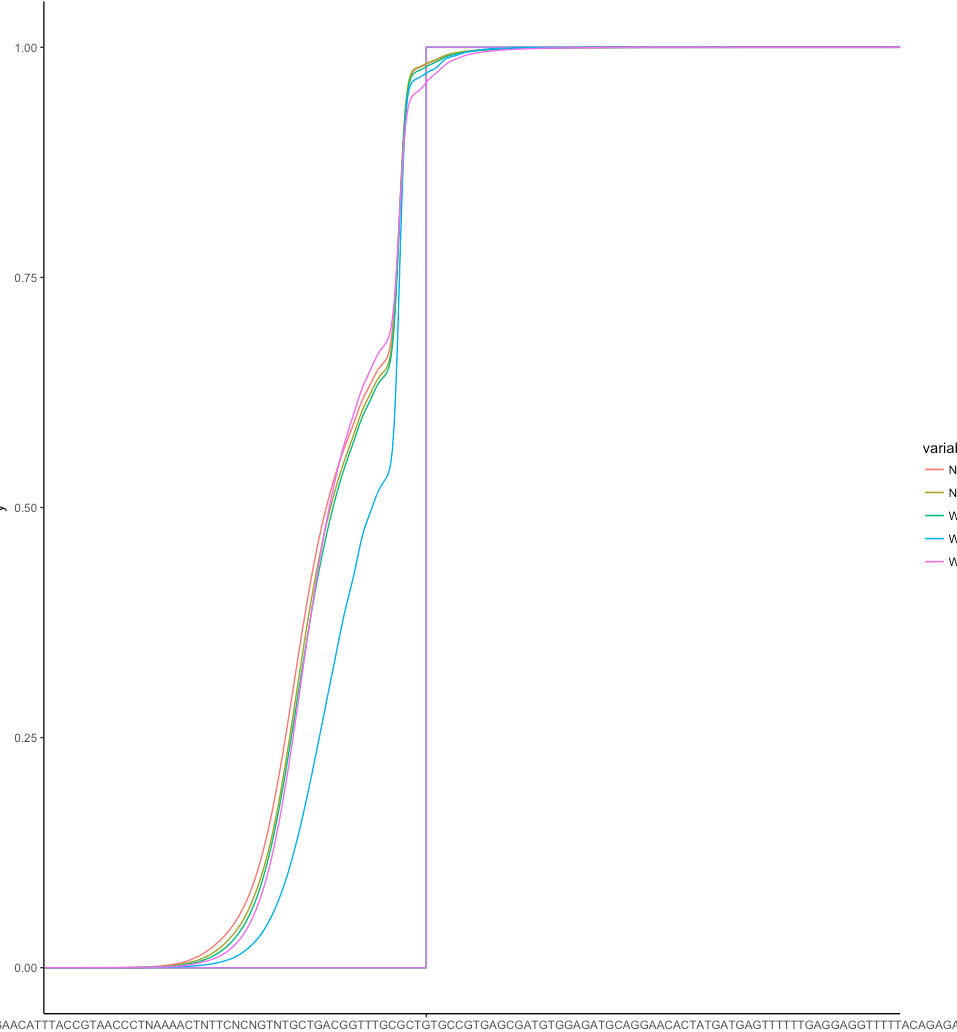
Сюжет выглядит так,
Как получить плавную кривую? Нужно ли выполнять более статистическую операцию, чтобы получить это?
обновленный код
ir.d = as.data.frame(ir.m)
denss = split(ir.d, ir.d$variable) %>%
map_df(function(dw) {
denss = density(dw$value, from=min(ir.d$value) - 0.05*diff(range(ir.d$value)),
to=max(ir.d$value) + 0.05*diff(range(ir.d$value)))
data.frame(x=denss$x, y=denss$y, cd=cumsum(denss$y)/sum(denss$y), group=dw$variable[1])
head(denss)
})
summary(denss)
> summary(denss)
x y cd group
Min. :-13.689 Min. :0.0000000 Min. :0.00000 N1.ir:512
1st Qu.: -5.466 1st Qu.:0.0000046 1st Qu.:0.07061 N2.ir:512
Median : 2.757 Median :0.0002487 Median :0.99552 W1.ir :512
Mean : 2.757 Mean :0.0303942 Mean :0.65315 W2.ir :512
3rd Qu.: 10.980 3rd Qu.:0.0148074 3rd Qu.:0.99997 W3.ir :512
Max. : 19.203 Max. :0.9440592 Max. :1.00000
сюжет
ggplot() +
stat_ecdf(data=ir.d, aes(x, colour=variable), alpha=0.8) +
geom_line(data=denss, aes(x, cd, colour=group)) +
theme_classic()
1 ответ
ECDF следует за данными точно, без сглаживания. Однако вы можете создать сглаженную совокупную плотность, сгенерировав из данных оценку плотности ядра (в основном сглаженную гистограмму) и создав из нее "ecdf". Вот пример с поддельными данными:
Сначала мы генерируем оценку плотности ядра, используя density функция. По умолчанию это дает нам оценку плотности на сетке из 512 значений x. Затем мы используем это как "данные" для вычисления ecdf, которое является просто кумулятивной суммой плотности (или, для любой заданной точки a вдоль оси x, значение ecdf в a является областью под плотностью ядра). кривая (то есть интеграл) от -Inf до а).
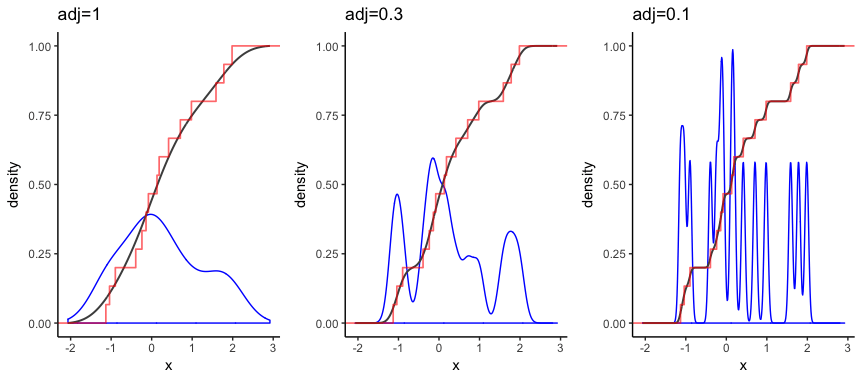
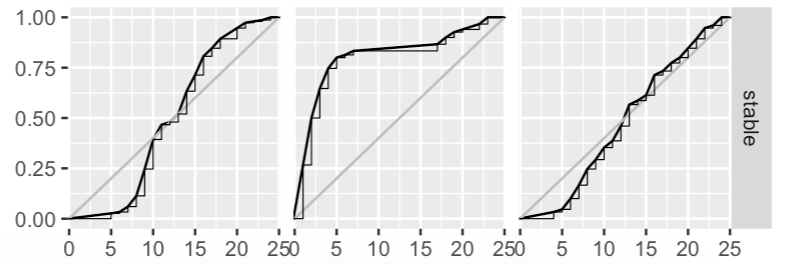
Я pacakaged код в функцию ниже, чтобы вы могли видеть, как изменение adjust Параметр функции плотности изменяет сглаженный ecdf. Меньшее значение adjust уменьшает степень сглаживания, создавая оценку плотности, которая более точно соответствует данным. Вы можете увидеть на графиках ниже этого параметра adj=0.1 приводит к меньшему сглаживанию сглаженного ecdf, так что он более точно следует этапу исходного ecdf.
library(ggplot2)
smooth_ecd = function(adj = 1) {
# Fake data
set.seed(2)
dat = data.frame(x=rnorm(15))
# Extend range of density estimate beyond data
e = 0.3 * diff(range(dat$x))
# Kernel density estimate of fake data
dens = density(dat$x, adjust=adj, from=min(dat$x)-e, to=max(dat$x) +e)
dens = data.frame(x=dens$x, y=dens$y)
# Plot kernel density (blue), ecdf (red) and smoothed ecdf (black)
ggplot(dat, aes(x)) +
geom_density(adjust=adj, colour="blue", alpha=0.7) +
geom_line(data=dens, aes(x=x, y=cumsum(y)/sum(y)), size=0.7, colour='grey30') +
stat_ecdf(colour="red", size=0.6, alpha=0.6) +
theme_classic() +
labs(title=paste0("adj=",adj))
}
smooth_ecd(adj=1)
smooth_ecd(adj=0.3)
smooth_ecd(adj=0.1)
Вот некоторый код для того, чтобы сделать это группой:
library(tidyverse)
# Fake data with two groups
set.seed(2)
dat = data.frame(x=c(rnorm(15, 0, 1), rnorm(20, 0.2, 0.8)),
group=rep(LETTERS[1:2], c(15,20)))
# Split the data by group and calculate the smoothed cumulative density for each group
dens = split(dat, dat$group) %>%
map_df(function(d) {
dens = density(d$x, adjust=0.1, from=min(dat$x) - 0.05*diff(range(dat$x)),
to=max(dat$x) + 0.05*diff(range(dat$x)))
data.frame(x=dens$x, y=dens$y, cd=cumsum(dens$y)/sum(dens$y), group=d$group[1])
})
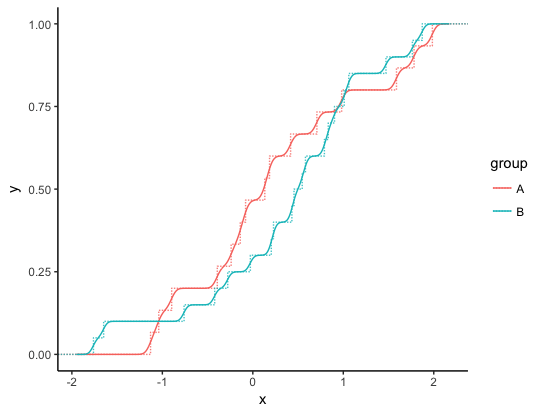
Теперь мы можем построить каждую сглаженную совокупную плотность. На графике ниже я включил звонок stat_ecdf с исходными данными для сравнения.
ggplot() +
stat_ecdf(data=dat, aes(x, colour=group), alpha=0.8, lty="11") +
geom_line(data=dens, aes(x, cd, colour=group)) +
theme_classic()
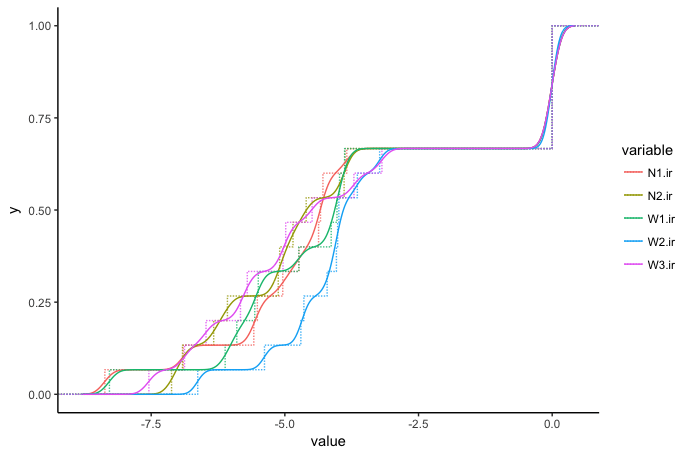
ОБНОВЛЕНИЕ: Используя ваш образец данных, вот что я получаю. Я понятия не имею, как вы получили эту длинную нуклеотидную строку в качестве значения x на вашем графике, поскольку такая переменная не появляется нигде в опубликованных вами данных.
# Melt data
dat = gather(df, variable, value, -junc)
# Split the data by group and calculate the smoothed cumulative density for each group
dens = split(dat, dat$variable) %>%
map_df(function(d) {
dens = density(d$value, adjust=0.1, from=min(dat$value) - 0.05*diff(range(dat$value)),
to=max(dat$value) + 0.05*diff(range(dat$value)))
data.frame(x=dens$x, y=dens$y, cd=cumsum(dens$y)/sum(dens$y), group=d$variable[1])
})
ggplot() +
stat_ecdf(data=dat, aes(value, colour=variable), alpha=0.8, lty="11") +
geom_line(data=dens, aes(x, cd, colour=group)) +
theme_classic()
Это более старая ветка, однако я просто хочу упомянуть, что stat_ecdf(..., geom = "line") может быть подходящим решением для некоторых людей, чтобы избежать шагов из geom_stepна кривой ecdf. -Майкл