Разница между умножением numpy dot() и умножением матриц Python 3.5+.
Недавно я перешел на Python 3.5 и заметил, что новый оператор умножения матриц (@) иногда ведет себя не так, как оператор NumPy. Например, для 3d-массивов:
import numpy as np
a = np.random.rand(8,13,13)
b = np.random.rand(8,13,13)
c = a @ b # Python 3.5+
d = np.dot(a, b)
@ Оператор возвращает массив формы:
c.shape
(8, 13, 13)
в то время как np.dot() функция возвращает:
d.shape
(8, 13, 8, 13)
Как я могу воспроизвести тот же результат с NumPy точка? Есть ли другие существенные различия?
3 ответа
@ Оператор вызывает массив __matmul__ метод, а не dot, Этот метод также присутствует в API как функция np.matmul,
>>> a = np.random.rand(8,13,13)
>>> b = np.random.rand(8,13,13)
>>> np.matmul(a, b).shape
(8, 13, 13)
Из документации:
matmulотличается отdotдвумя важными способами.
- Умножение на скаляры не допускается.
- Стеки матриц передаются вместе, как если бы матрицы были элементами.
Последний пункт проясняет, что dot а также matmul методы ведут себя по-разному, когда передаются трехмерные (или более объемные) массивы. Цитирую из документации еще немного:
За matmul:
Если один из аргументов равен ND, N > 2, он обрабатывается как стек матриц, находящихся в последних двух индексах, и транслируется соответствующим образом.
За np.dot:
Для двумерных массивов это эквивалентно умножению матриц, а для одномерных массивов - на внутреннее произведение векторов (без комплексного сопряжения). Для N измерений это сумма произведений по последней оси а и второй по длине б
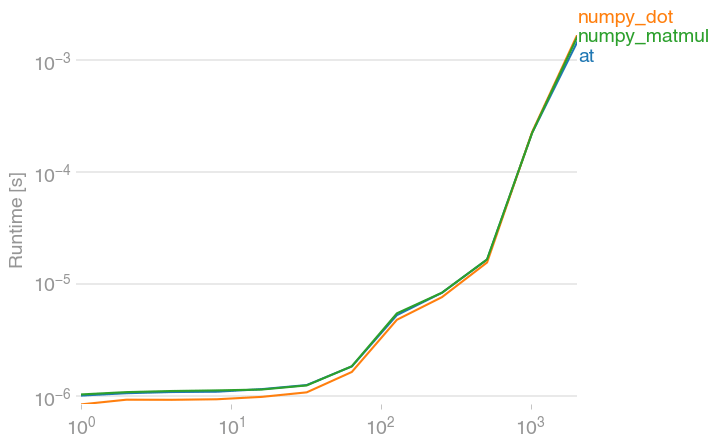
Просто к вашему сведению, @ и его эквиваленты numpy dot а также matmulвсе примерно одинаково быстры. (Сюжет создан с помощью моего проекта perfplot.)
Код для воспроизведения сюжета:
import perfplot
import numpy
def setup(n):
A = numpy.random.rand(n, n)
x = numpy.random.rand(n)
return A, x
def at(data):
A, x = data
return A @ x
def numpy_dot(data):
A, x = data
return numpy.dot(A, x)
def numpy_matmul(data):
A, x = data
return numpy.matmul(A, x)
perfplot.show(
setup=setup,
kernels=[at, numpy_dot, numpy_matmul],
n_range=[2 ** k for k in range(12)],
logx=True,
logy=True,
)
Ответ @ajcr объясняет, как dot а также matmul (вызывается @ символ) отличаются. Рассматривая простой пример, мы ясно видим, как они ведут себя по-разному при работе со "стеками матриц" или тензорами.
Чтобы выяснить различия, возьмите массив 4x4 и верните dot продукт и matmul продукт со стеком матриц 2x4x3 или тензором.
import numpy as np
fourbyfour = np.array([
[1,2,3,4],
[3,2,1,4],
[5,4,6,7],
[11,12,13,14]
])
twobyfourbythree = np.array([
[[2,3],[11,9],[32,21],[28,17]],
[[2,3],[1,9],[3,21],[28,7]],
[[2,3],[1,9],[3,21],[28,7]],
])
print('4x4*4x2x3 dot:\n {}\n'.format(np.dot(fourbyfour,twobyfourbythree)))
print('4x4*4x2x3 matmul:\n {}\n'.format(np.matmul(fourbyfour,twobyfourbythree)))
Продукты каждой операции указаны ниже. Обратите внимание, как точечный продукт,
... сумма произведений по последней оси а и второй к последней б
и как матричное произведение формируется путем совместного вещания матрицы.
4x4*4x2x3 dot:
[[[232 152]
[125 112]
[125 112]]
[[172 116]
[123 76]
[123 76]]
[[442 296]
[228 226]
[228 226]]
[[962 652]
[465 512]
[465 512]]]
4x4*4x2x3 matmul:
[[[232 152]
[172 116]
[442 296]
[962 652]]
[[125 112]
[123 76]
[228 226]
[465 512]]
[[125 112]
[123 76]
[228 226]
[465 512]]]
В математике, я думаю, что точка в NumPy имеет больше смысла
точка(a,b)_{i,j,k,a,b,c} = \sum_m a_{i,j,k,m}b_{a,b,m,c}
поскольку он дает скалярное произведение, когда a и b являются векторами, или умножение матриц, когда a и b являются матрицами
Что касается операции matmul в numpy, она состоит из частей результата точки и может быть определена как
matmul(a, b) _ {i, j, k, c} = \ sum_m a_ {i, j, k, m} b_ {i, j, m, c}
Итак, вы можете видеть, что matmul(a,b) возвращает массив с небольшой формой, который имеет меньшее потребление памяти и имеет больше смысла в приложениях. В частности, в сочетании с вещанием вы можете получить
matmul(a, b) _ {i, j, k, l} = \ sum_m a_ {i, j, k, m} b_ {j, m, l}
например.
Из приведенных выше двух определений вы можете видеть требования для использования этих двух операций. Предположим, что a.shape=(s1,s2,s3,s4) и b.shape=(t1,t2,t3,t4)
Чтобы использовать точку (а, б) вам нужно
1. **t3=s4**;Чтобы использовать Matmul (A, B) вам нужно
- t3 = s4
- t2 = s2 или один из t2 и s2 равен 1
- t1 = s1 или один из t1 и s1 равен 1
Используйте следующий фрагмент кода, чтобы убедить себя.
Пример кода
import numpy as np
for it in xrange(10000):
a = np.random.rand(5,6,2,4)
b = np.random.rand(6,4,3)
c = np.matmul(a,b)
d = np.dot(a,b)
#print 'c shape: ', c.shape,'d shape:', d.shape
for i in range(5):
for j in range(6):
for k in range(2):
for l in range(3):
if not c[i,j,k,l] == d[i,j,k,j,l]:
print it,i,j,k,l,c[i,j,k,l]==d[i,j,k,j,l] #you will not see them
Вот сравнение с np.einsum показать, как прогнозируются индексы
np.allclose(np.einsum('ijk,ijk->ijk', a,b), a*b) # True
np.allclose(np.einsum('ijk,ikl->ijl', a,b), a@b) # True
np.allclose(np.einsum('ijk,lkm->ijlm',a,b), a.dot(b)) # True
Мой опыт работы с MATMUL и DOT
Я постоянно получал "ValueError: форма переданных значений (200, 1), индексы подразумевают (200, 3)" при попытке использовать MATMUL. Я хотел найти быстрое решение и обнаружил, что DOT предоставляет ту же функциональность. Я не получаю ошибок при использовании DOT. Я получаю правильный ответ
с MATMUL
X.shape
>>>(200, 3)
type(X)
>>>pandas.core.frame.DataFrame
w
>>>array([0.37454012, 0.95071431, 0.73199394])
YY = np.matmul(X,w)
>>> ValueError: Shape of passed values is (200, 1), indices imply (200, 3)"
с DOT
YY = np.dot(X,w)
# no error message
YY
>>>array([ 2.59206877, 1.06842193, 2.18533396, 2.11366346, 0.28505879, …
YY.shape
>>> (200, )